9.4: Surface Area
- Page ID
- 2170
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Surface Area and Nets
In geometry, a net is a 2-dimensional shape that can be folded to form a 3-dimensional shape or a solid. Or a net is a drawing made when the surface of a 3-dimensional figure is laid out flat showing each face and edge of the figure in 2-dimension.
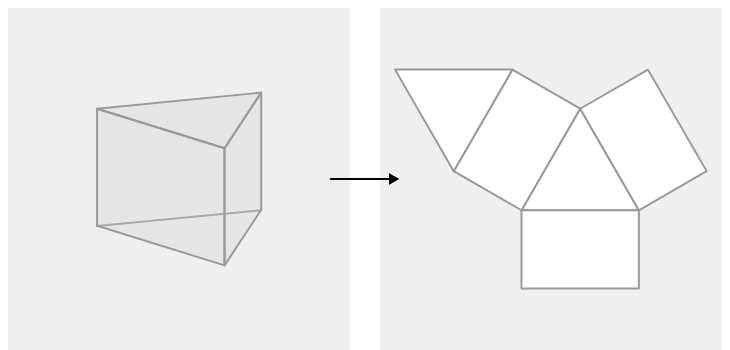
Here are some steps to determine whether a net forms a solid:
1. Make sure that the solid and the net have the same number of faces and that the shapes of the faces of the solid match the shapes of the corresponding faces in the net.
2. Visualize how the net is to be folded to form the solid and make sure that all the sides fit together properly.
Nets are helpful when we need to find the surface area of the solids. In the image above, you can see a triangular prism when unfolded consists of two triangles and three rectangles. The triangles are the bases of the prism and the rectangles are the lateral faces.
Surface Area of a Solid
The surface area of a 3-dimensional object is the measure of the total area of all its faces. This means that one way to find the surface area of a solid is to find the area of its net.
\(Surface\: area\: of\: rectangular\: prism=2ab+2ac+2bc=2(ab+ac+bc)\)
The surface area of a rectangular prism is the area of the six rectangles that cover it. But we don't have to figure out all six because we know that the top and bottom are the same, the front and back are the same, and the left and right sides are the same.
Nets of Solids
Explore the nets and see how the 2d shape transforms into a 3d shape.

Note that there could be a couple different interpretations of any net. Most prisms have multiple nets.
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Find the approximate surface area of the triangular prism below. The base is an equilateral triangle.
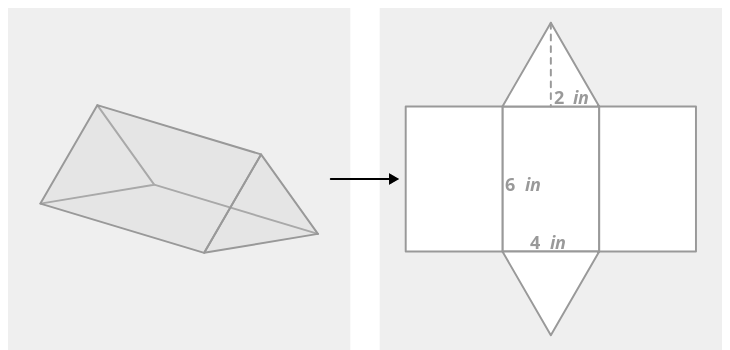
The net is made of three congruent rectangles and two congruent equilateral triangles.
The surface area is the sum of the areas of the five shapes. To find the area of the triangle, you need to know the height of the triangle. Using the Pythagorean Theorem, you can determine that the height is approximately 3.46 inches.
\(H^2=P^2+B^2\)
\(4^2=P^2+2^2\)
\(P^2=16−4=12\)
\(P=3.46 inches\)

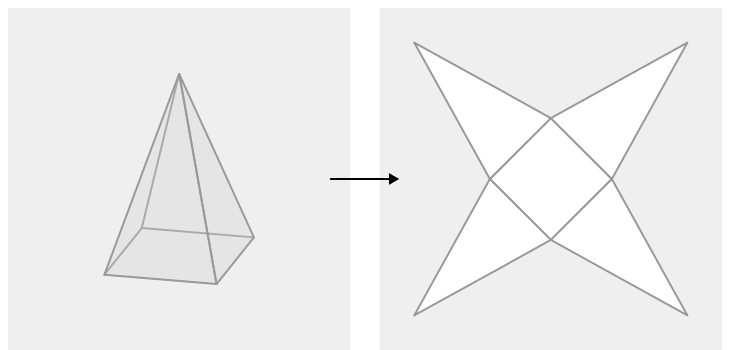
Draw the net of a square pyramid.
A square pyramid has a height of 20 inches. Each side of the square base is 12 inches. What is the surface area of the pyramid?
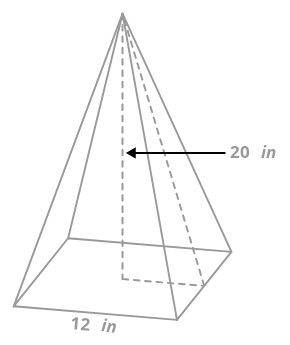
In order to find the surface area, you will need to determine the area of the triangle faces. In order to find the area of each triangle face, you will need the base and height of the triangle. In order to do this, imagine a right triangle standing upright in the pyramid.
The height of this triangle is 20 inches and the base of the triangle is 6 inches. It's hypotenuse, which is the height of the triangle face, can be determined with the Pythagorean Theorem.
Now you can find the area of each of the five shapes that make up the net in order to find the surface area.

\(H^2=P^2+B^2\)
\(H^2=20^2+6^2\)
\(H^2=400+36\)
\(H=\sqrt{436}=20.88 inches

Identify the solid whose net is given below, based on the base shape.
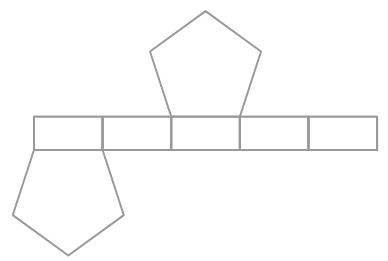
The solid is _______.
CK-12 PLIX: Cross-Sections and Nets
Interactive Element
Example \(\PageIndex{1}\)
A cup of paint covers about 22 square feet. You need to paint all faces of a cube to use as a prop in a play. Each edge of the cube is 2.5 feet long. How much paint will you need to buy?
Solution
One cup of paint covers about 22 square feet. Each edge of the cube is 2.5 feet long. In order to figure out how much paint you will need, you should find the surface area of the cube.
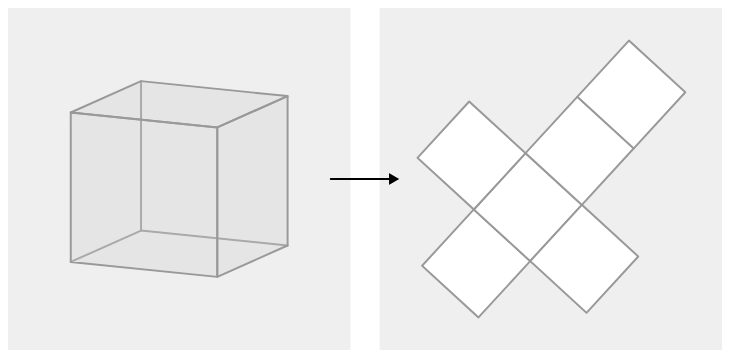
The cube has six congruent square faces. The area of each square is \((2.5)^2=6.25 ft^2\). The total surface area of the cube is \(37.5 ft^2\). You will need \(37.522\approx 1.7\) cups of paint.
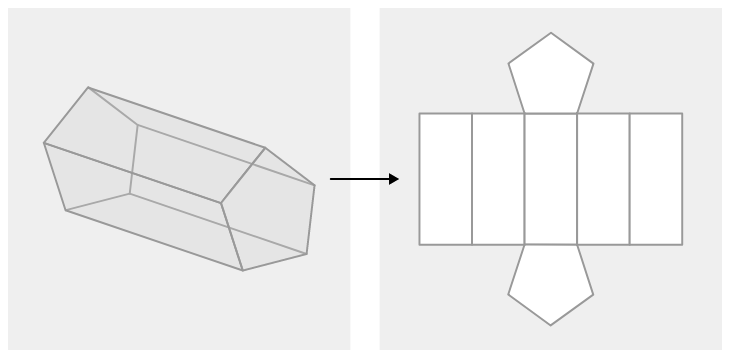
Example \(\PageIndex{2}\)
Draw the net for a pentagonal prism.
Solution
Example \(\PageIndex{3}\)
The base of a pentagonal prism is the following pentagon:
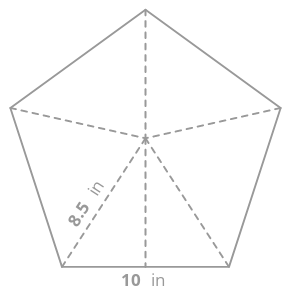
Find the area of the pentagon by dissecting the pentagon into five triangles and finding the area of each triangle.
Solution
Use the Pythagorean Theorem to find the height of each triangle.
\(H^2=P^2+B^2\)
\(8.5^2=P^2+5^2\)
\(P^2=72.25−25=47.25\)
\(P=\sqrt{47.25}=6.87 inches\)

Example \(\PageIndex{4}\)
Find the surface area for a pentagonal prism with a height of 25 inches and a base given in Example 3.

Solution
The pentagonal prism is made of five rectangular faces and two pentagonal faces. Each rectangle is 10 inches by 25 inches.

Review
1. Explain the connection between the surface area of a solid and the net of a solid.
2. When stating a surface area, why do you use square units such as "\(in^2\)"?
A triangular pyramid has four congruent equilateral triangle faces. Each edge of the pyramid is 6 inches.
3. Draw a net for the pyramid.
4. Find the area of one triangle face.
5. Find the surface area of the pyramid.
A 20 inch tall hexagonal pyramid has a regular hexagon base that can be divided into six equilateral triangles with side lengths of 12 inches, as shown below.
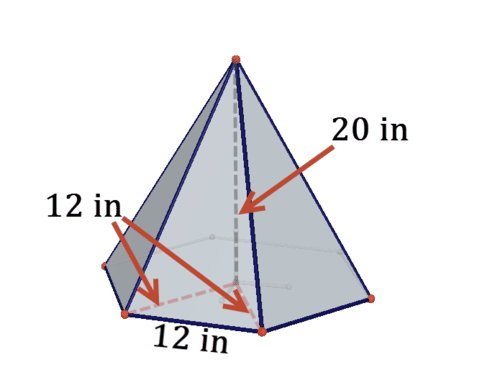
6. Draw a net for the pyramid.
7. Find the area of the hexagon base.
8. The pyramid has 6 triangular faces. Use the Pythagorean Theorem to help you to find the height of each of these triangles.
9. Find the total surface area of the pyramid.
A square prism is topped with a square pyramid to create the composite solid below.
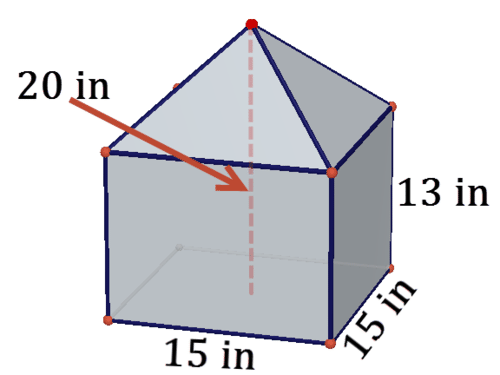
10. Draw a net for the solid.
11. There are four triangular faces. Use the Pythagorean Theorem to help you find the height of each of these triangles.
12. Find the total surface area of the solid.
A solid has the following net.
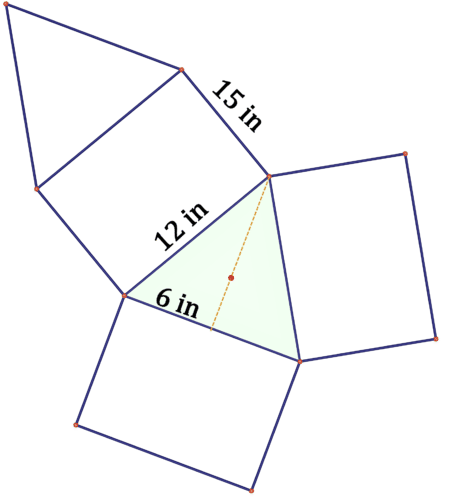
13. What type of solid is this?
14. Find the surface area of the solid.
15. What would the net of a cylinder look like? Try to make a sketch.
16. What would the net of a cone look like? Try to make a sketch.
16. Graph the points \((2,3)\) and \((12,3)\). Label them A and B and connect them to form a segment. Draw vertical segments connecting them to the \(x\)-axis. Rotate this shape around the \(x\)-axis to form a solid. What figure have you made? Explain. Find the surface area and volume of this figure.
17. Graph the points \((2,0)\) and \((10,6)\). Label them A and B and connect them to form a segment. Draw a vertical segment from B to the \(x\)-axis. Rotate this shape around the \(x\)-axis to form a solid. What figure have you made? Explain. Find the surface area and volume of this figure.
18. Graph the points \((24,10)\) and \((12,5)\). Form a solid of revolution as described above. Find its surface area and volume.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.11.
Additional Resources
Interactive Element
Practice: Surface Area

