9.3: Cross-Sections and Nets
- Page ID
- 2168
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cross-sections are intersections of a plane with a solid. Nets are unfolded, flat representations of the sides of a 3-D shape that allow you to find the sum of the area of the faces by showing the edges and faces in 2-D.
While our world is three dimensional, we are used to modeling and thinking about three dimensional objects on paper (in two dimensions). There are a few common ways to help think about three dimensions in two dimensions. One way to “view” a three-dimensional figure in a two-dimensional plane (like on a piece of paper or a computer screen) is to use cross-sections. Another way to “view” a three-dimensional figure in a two-dimensional plane is to use a net.
Cross-Section: The intersection of a plane with a solid.
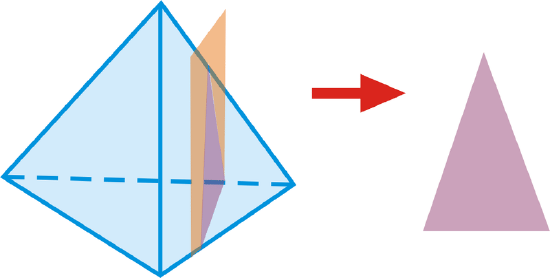
The cross-section of the peach plane and the tetrahedron is a triangle.
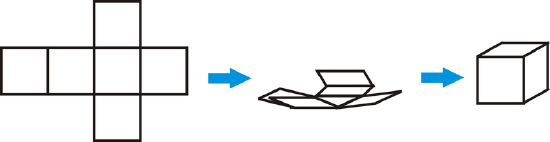
Net: An unfolded, flat representation of the sides of a three-dimensional shape.
It is good to be able to visualize cross sections and nets as the three dimensional objects they represent.
What if you were given a three-dimensional figure like a pyramid and you wanted to know what that figure would look like in two dimensions? What would a flat slice or an unfolded flat representation of that solid look like?
Example \(\PageIndex{1}\)
Describe the cross section formed by the intersection of the plane and the solid.
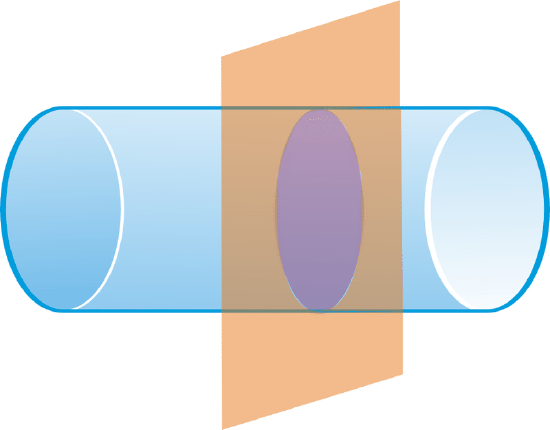
Solution
Circle
Example \(\PageIndex{2}\)
Determine what shape is formed by the following net.
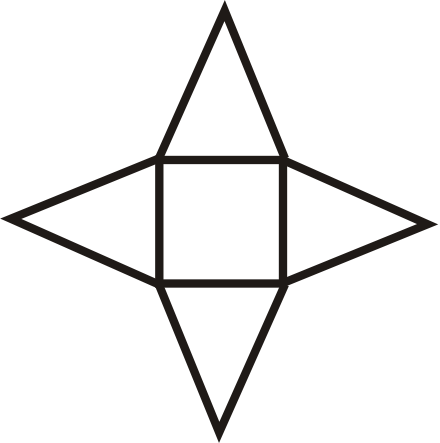
Solution
Square-based pyramid
Example \(\PageIndex{3}\)
What is the shape formed by the intersection of the plane and the regular octahedron?
-
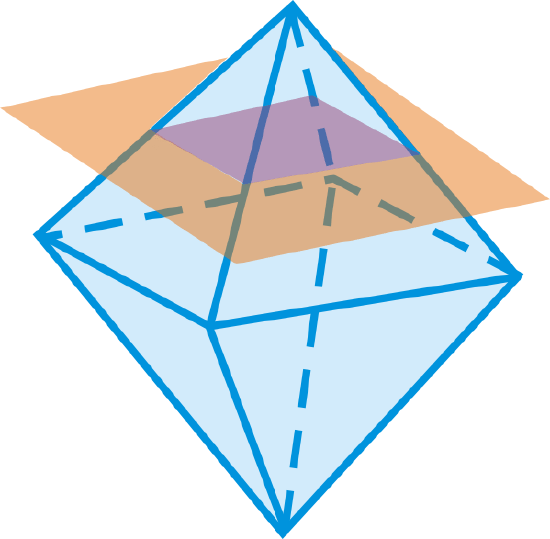
Figure \(\PageIndex{5}\) -
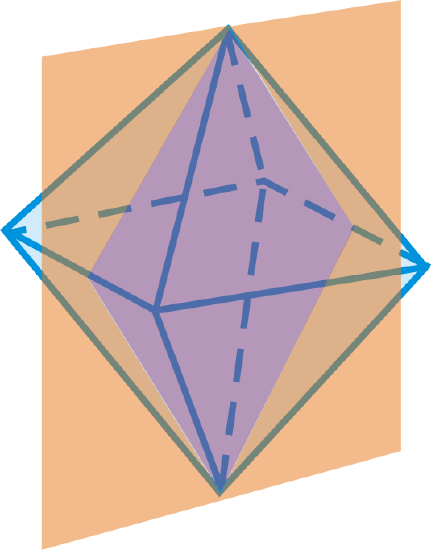
Figure \(\PageIndex{6}\) -
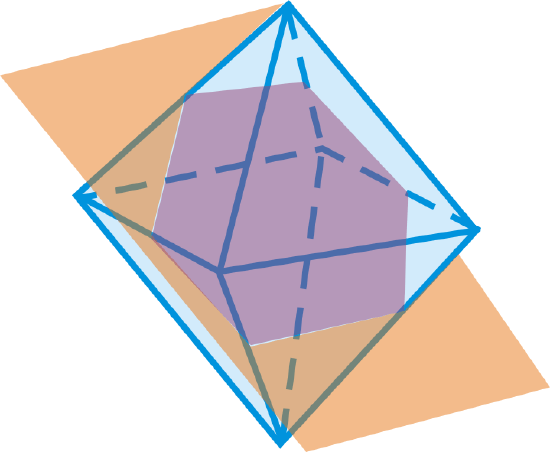
Figure \(\PageIndex{7}\
Solution
- Square
- Rhombus
- Hexagon
Example \(\PageIndex{4}\)
What kind of figure does this net create?
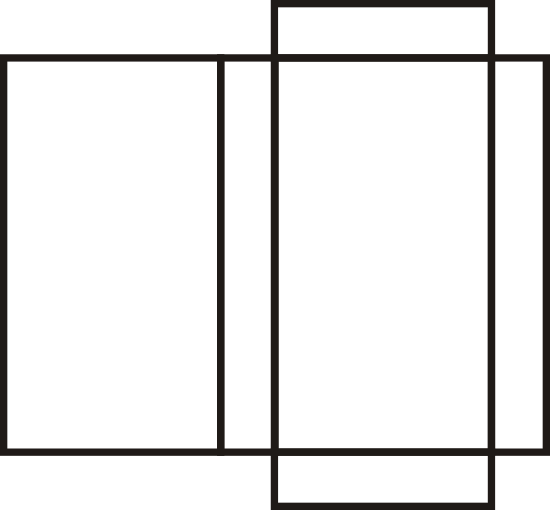
Solution
The net creates a rectangular prism.
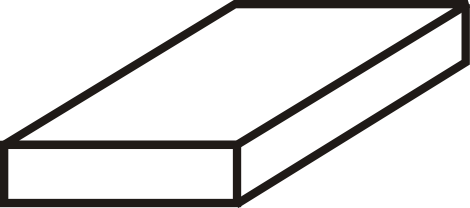
Example \(\PageIndex{5}\)
Draw a net of the right triangular prism below.
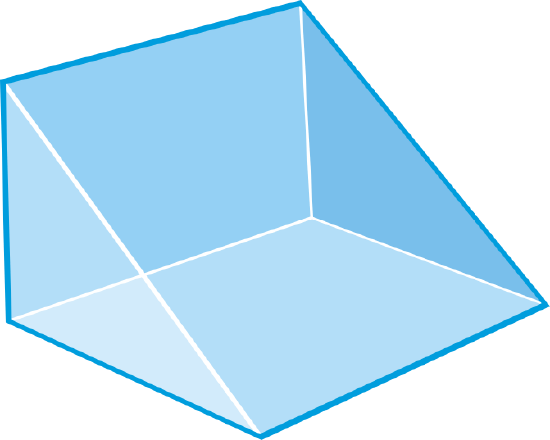
Solution
The net will have two triangles and three rectangles. The rectangles are different sizes and the two triangles are the same.
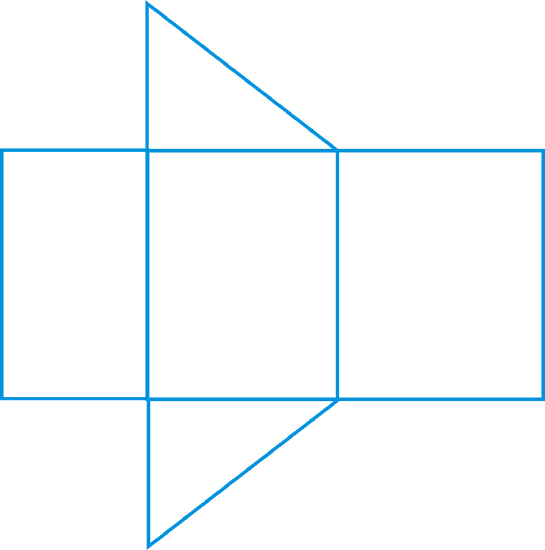
There are several different nets of any polyhedron. For example, this net could have the triangles anywhere along the top or bottom of the three rectangles.
Review
Describe the cross section formed by the intersection of the plane and the solid.
-
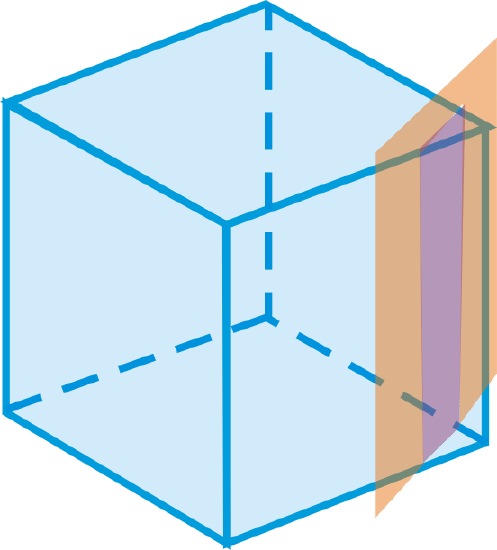
Figure \(\PageIndex{12}\) -
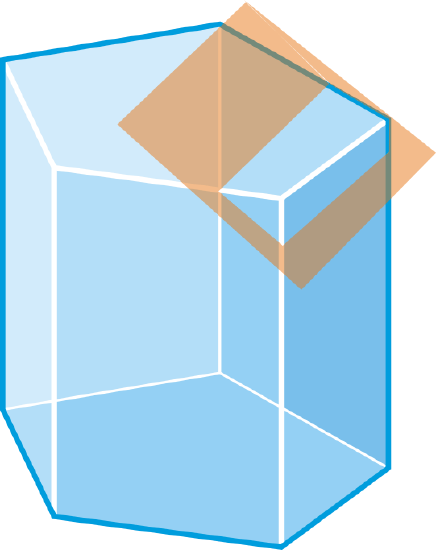
Figure \(\PageIndex{13}\)
Draw the net for the following solids.
-
Figure \(\PageIndex{14}\) -
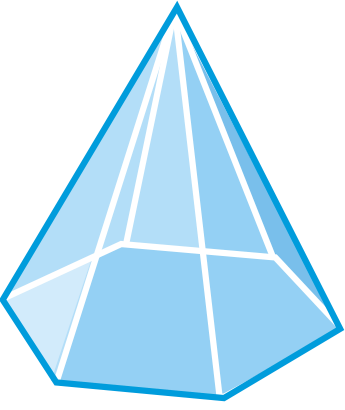
Figure \(\PageIndex{15}\) -
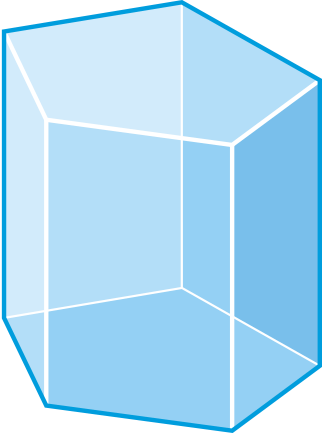
Figure \(\PageIndex{16}\) -
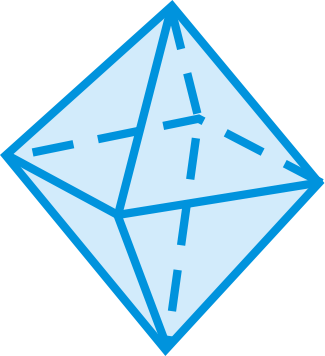
Figure \(\PageIndex{17}\) -
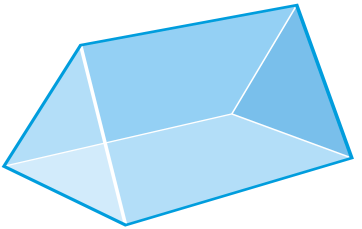
Figure \(\PageIndex{18}\) -
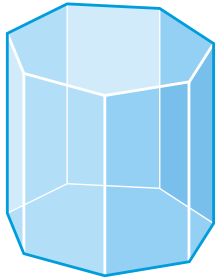
Figure \(\PageIndex{19}\)
Determine what shape is formed by the following nets.
-
Figure \(\PageIndex{20}\) -
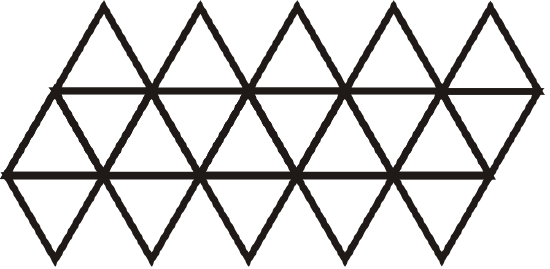
Figure \(\PageIndex{21}\) -
Figure \(\PageIndex{22}\) -
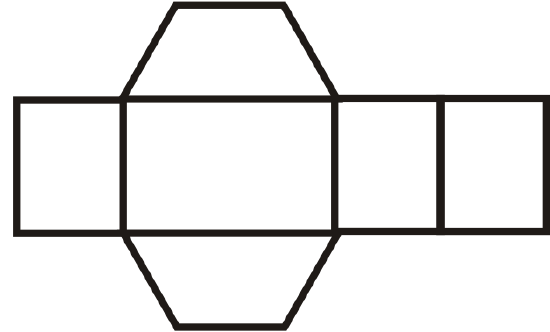
Figure \(\PageIndex{23}\
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.2.
Vocabulary
| Term | Definition |
|---|---|
| cross-section | The intersection of a plane with a solid. |
| net | An unfolded, flat representation of the sides of a three-dimensional shape. |
| cross section | A cross section is the intersection of a three-dimensional solid with a plane. |
| Polyhedron | A polyhedron is a solid with no curves surfaces or edges. All faces are polygons and all edges are line segments. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |