2.4.4: Definition of Inverse Reciprocal Trig Functions

Inverse secant, cosecant, and cotangent functions.

So far you've had to deal with trig functions, reciprocal functions, and inverse functions. Now you'll start to see inverse reciprocal functions. For example, can you compute

\(\sec^{−1} \dfrac{2}{\sqrt{3}}\)

As it turns out, this can be readily computed.

Inverse Reciprocal Trigonometric Functions

We already know that the cosecant function is the reciprocal of the sine function. This will be used to derive the reciprocal of the inverse sine function.

\(\begin{aligned} y&=\sin^{−1} x\\ x&=\sin y \\ \dfrac{1}{x}&=\csc y \\ \csc ^{−1} \dfrac{1}{x}&= y\\ \csc ^{−1} \dfrac{1}{x}&= \sin^{−1} x \end{aligned}\)

Because cosecant and secant are inverses, \(\sin^{−1}\dfrac{1}{x}=\csc ^{−1} x\) is also true.

The inverse reciprocal identity for cosine and secant can be proven by using the same process as above. However, remember that these inverse functions are defined by using restricted domains and the reciprocals of these inverses must be defined with the intervals of domain and range on which the definitions are valid.

\(\sec^{−1}\dfrac{1}{x}=\cos ^{−1}x \leftrightarrow \cos ^{−1}\dfrac{1}{x}=\sec^{−1} x\)

Tangent and cotangent have a slightly different relationship. Recall that the graph of cotangent differs from tangent by a reflection over the y−axis and a shift of \(\dfrac{\pi}{2}\). As an equation, this can be written as \(\cot x=−\tan\left(x−\dfrac{\pi}{2}\right)\). Taking the inverse of this function will show the inverse reciprocal relationship between arccotangent and arctangent.

\(\begin{aligned}
y &=\sin ^{-1} x \\
x &=\sin y \\
\frac{1}{x} &=\csc y \\
\csc ^{-1} \frac{1}{x} &=y \\
\csc ^{-1} \frac{1}{x} &=\sin ^{-1} x
\end{aligned}\)

Remember that tangent is an odd function, so that \(\tan(−x)=-\tan(x)\). Because tangent is odd, its inverse is also odd. So, this tells us that \(\cot^{−1} x=\dfrac{\pi}{2}−\tan^{−1}x\) and \(\tan^{−1}x=\dfrac{\pi}{2}−\cot^{−1}x\). To graph arcsecant, arccosecant, and arccotangent in your calculator you will use these conversion identities: \(\sec^{−1}x=\cos ^{−1} \dfrac{1}{x}\), \(\csc ^{−1} x=\sin^{−1}\dfrac{1}{x}\), \(\cot^{−1} x=\dfrac{\pi}{2}−\tan^{−1} x\). Note: It is also true that \(\cot^{−1}x=\tan^{−1}\dfrac{1}{x}\).

Finding the Inverse

Find the inverse of \(\sec^{−1}\sqrt{2}\)

Use the inverse reciprocal property. \(\sec^{−1}x=\cos ^{−1}\dfrac{1}{x}\rightarrow \sec^{−1} \sqrt{2}=\cos ^{−1}\dfrac{1}{\sqrt{2}}\)

Recall that \(\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\). So, \(\sec^{−1}\sqrt{2}=\cos ^{−1}\dfrac{\sqrt{2}}{2}\), and we know that \(\cos ^{−1}\dfrac{\sqrt{2}}{2}=\dfrac{\pi}{4}\). Therefore, \(\sec^{−1}\sqrt{2}=\dfrac{\pi}{4}\).

Finding the Exact Value

For each of these problems, first find the reciprocal and then determine the angle from that (without a calculator).

1. \(\sec^{−1}\sqrt{2}\)

\(\sec^{−1}\sqrt{2}=\cos ^{−1}\dfrac{\sqrt{2}}{2}\) From the unit circle, we know that the answer is \(\dfrac{\pi}{4}\).

2. \(\cot^{−1}(−\sqrt{3})\)

\(\cot^{−1}(−\sqrt{3})=\dfrac{\pi}{2}−\tan^{−1}(−\sqrt{3})\) From the unit circle, the answer is \(\dfrac{5\pi}{6}\).

3. \(\csc ^{−1}\dfrac{2\sqrt{3}}{3}\)

\(\csc ^{−1}\dfrac{2}{\sqrt{3}}3=\sin^{−1}\dfrac{\sqrt{3}}{2}\) Within our interval, there are is one answer, \(\dfrac{\pi}{3}\).

Using Technology

Make sure that your calculator’s MODE is RAD (radians)

1. \(\arcsin 0.6384\)

Figure \(\PageIndex{1}\)

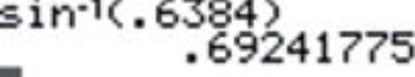
2. \(\arccos (−0.8126)\)

Figure \(\PageIndex{2}\)

3. \(\arctan (−1.9249)\)

Figure \(\PageIndex{3}\)

Example \(\PageIndex{1}\)

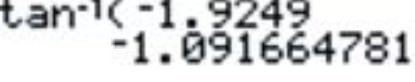
Earlier, you were asked to evaluate \(\sec^{−1} \dfrac{2}{\sqrt{3}}\)

Solution

You can start with the inverse reciprocal property:

\(\sec^{−1}x=\cos ^{−1} \dfrac{1}{x}\)

Substituting in values for "x\)" gives:

\(\sec^{−1}\dfrac{2}{\sqrt{3}}=\cos ^{−1}\dfrac{1}{\dfrac{2}{\sqrt{3}}}\)

This can be rewritten as:

\(\cos ^{−1}\dfrac{\sqrt{3}}{2}\)

And

\(\cos ^{−1} \dfrac{\sqrt{3}}{2}=\dfrac{\pi}{6}\)

Therefore,

\(\sec^{−1} \dfrac{2}{\sqrt{3}}=\dfrac{\pi}{6}\)

Example \(\PageIndex{2}\)

Evaluate \(\sec^{−1}(−2)\)

Solution

\(\dfrac{2 \pi}{3}\)

Example \(\PageIndex{3}\)

Evaluate \(\cot^{−1}(−1)\)

Solution

\(−\dfrac{\pi}{4}\)

Example \(\PageIndex{4}\)

Evaluate \(\csc ^{−1}(\sqrt{2})\)

Solution

\(\dfrac{\pi}{4}\)

Review

Using technology, find the value in radian measure, of each of the following.

1. \(\sin^{−1}(.345)\)
2. \(\cos ^{−1}(.87)\)
3. \(\csc ^{−1}(4)\)
4. \(\sec^{−1}(2.32)\)
5. \(\cot^{−1}(5.2)\)

Find the exact value of each expression within the restricted domain, without a calculator.

6. \(\sec^{−1}(\dfrac{2\sqrt{3}}{3})\)
7. \(\csc ^{−1}(1)\)
8. \(\cot^{−1}(\sqrt{3})\)
9. \(\csc ^{−1}(2)\)
10. \(\sec^{−1}(\sqrt{2})\)
11. \(\cot^{−1}(1)\)
12. \(\cos ^{−1}\left(\dfrac{1}{2}\right)\)
13. \(\sec^{−1}(2)\)
14. \(\cot^{−1}\left(\dfrac{\sqrt{3}}{3}\right)\)
15. \(\sin^{−1}\left(\dfrac{\sqrt{3}}{2}\right)\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 4.7.

Vocabulary

Term	Definition
inverse function	Inverse functions are functions that 'undo' each other. Formally \(f(x)\) and \(g(x)\) are inverse functions if \(f(g(x))=g(f(x))=x\).
Reciprocal Function	A reciprocal function is a function with the parent function \(y=\dfrac{1}{x}\).

Additional Resources

Video: Reciprocal Trig Functions

Practice: Definition of Inverse Reciprocal Trig Functions