1.4: 1.4 Domain and Range
- Page ID
- 951
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Analyze means to examine methodically and in detail. One way to analyze functions is by looking at possible inputs (domain) and possible outputs (range). Which of the basic functions have limited domains and why?
Domain and Range
Notation
Domain and range are described in interval notation. Parentheses, ( ), mean non-inclusive. Brackets, [ ], mean inclusive. The following descriptions of numbers into interval notation have been converted to interval notation.
1. All numbers.
\((-\infty, \infty)\) Note: Parentheses are always used with infinity.
2. All negative numbers not including 0.
\((-\infty, 0)\)
3. All positive numbers including 0.
\([0, \infty)\)
4. Every number between 1 and 4 including 1 and 4.
[1,4]
5. Every number between 5 and 6 not including 5 or 6.
(5, 6)
6. The numbers 1 through 2 including 1 but not including 2 and the numbers
10 through 25 including both 10 and 25
[1,2)\(\cup[10,25]\)
Note: The \(\cup\) symbol means Union and refers to the fact that if some number \(x\) is in this union, then it is either in the first group or it is in the second group. This symbol is associated with the OR statement. While it is true that the Union symbol seems to bring one group and another group together, the symbol for AND is \(\cap\) which means intersection. Intersection is different from union because intersection means all numbers that are in both the first group and second group at the same time.
Domain and Restricted Domain
Domain is the possible inputs to a function. Many functions allow any kind of numbers to be inputted. This includes numbers that are positive, negative, zero, fractions or decimals. The squaring function \(y=x^{2}\) is an example that has a domain of all possible real numbers. Three functions have very specific restrictions:
The square root function: \(y=\sqrt{x}\)
Domain restriction: \(x \geq 0\)
This is because the square root of a negative number is not a real number. This restriction can be observed in the graph because the curve ends at the point (0,0) and is not defined anywhere where \(x\) is negative.
The log function is only defined on numbers that are strictly bigger than zero. This is because the logarithmic function is a different way of writing exponents. One property of exponents is that any positive number raised to any power will never produce a negative number or zero. The restriction can be observed in the graph by the way the log function approaches the vertical line \(x=0\) and shoots down to infinity.
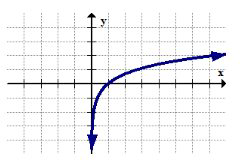
The reciprocal function: \(y=\frac{1}{x}\)
Domain Restriction: \(x \neq 0\)
The reciprocal function is restricted because you cannot divide numbers byzero. Any \(x\) values that make the denominator of a function zero are outside of the domain. This restriction can be observed in the graph by the way the reciprocal function never touches the vertical line \(x=0\).
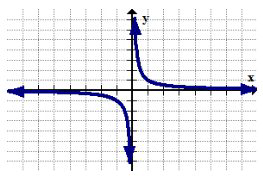
Range
Range is the possible outputs of a function. Just about any function can produce any output through the use of transformations and so determining the range of a function is significantly less procedural than determining the domain. Use what you know about the shape of each function and their equations to decide which \(y\) values are possible to produce and which \(y\) values are impossible to produce.
Finding Domain and Range
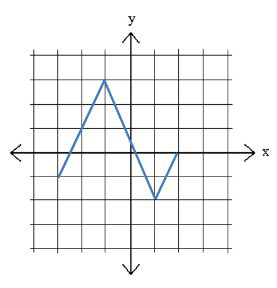
The domain and range for the graph above are:
Domain: \(x \in[-3,2]\)
Range: \(y \in[-2,3]\)
Note that the \(\in\) symbol means "is an element of" and means that the \(x\) or the \(y\) is in that interval and the numbers in the interval are always written in increasing order. [3,-2] is considered improper.
Note that even though the [-3,2] may look similar to the ordered pair that represents the point where \(x=-3\) and \(y=2,\) this is not the case. Both the -3 and the 2 are \(x\) values. This misconception is why you should always write \(x \in\) because it reminds you of this fact. Many people get very confused when they see something like \(x \in(-2,1)\) because they see the parenthesis and immediately see a point when they should see an interval on the \(x\) axis.
In the graph below, there are two different pieces of the function.
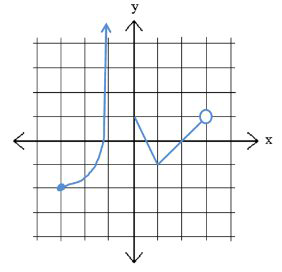
The domain and range for the graph above are:
Domain: \(x \in[-3,-1) \cup[0,3)\)
Range: \(y \in[-2, \infty)\)
The function seems to approach the vertical line \(x=-1\) without actually reaching it \(s 0\) an open bracket is used. Also, the empty hole at the point \((3,\) 1) which is why the domain excludes the \(x\) value of 3 .
Examples
Earlier, you were asked which basic functions have limited domains. The three functions that have limited domains are the square root function, the log function and the reciprocal function. The square root function has a restricted domain because you cannot take square roots of negative numbers and produce real numbers. The log function is restricted because the log function is not defined to operate on non-positive numbers. The reciprocal function is restricted because numbers that are divided by zero are not defined.
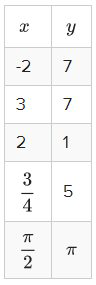
Identify the domain and range of the following function written in a table:
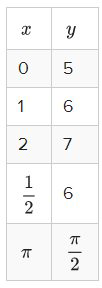
The specific equation of the function may be hidden, but from the table you can determine the domain and range directly from the \(x\) and \(y\) values. It may be tempting to guess that other values could potentially work in the table, especially if the pattern is obvious, but this is not the kind of question that asks what the function could be. Instead this question just asks what is the stated domain and range.
Domain: \(x \in\left\{0,1,2, \frac{1}{2}, \pi\right\}\)
Range: \(y \in\left\{5,6,7, \frac{\pi}{2}\right\}\)
Notice that the two 6’s that appear in the table do not need to be written twice in the range.
Identify the domain of the following three transformed functions.
1. \(y=10 \sqrt{2-x}-3\)
The argument of the function must be greater than or equal to 0.
\(\begin{aligned} 2-x & \geq 0 \\-x & \geq-2 \\ x & \leq 2 \end{aligned}\)
Domain: \(x \in(-\infty, 2]\)
2. \(y=\frac{3 x}{x^{2}+7 x+12}\)
The denominator cannot be equal to \(0 .\) First find what values of \(x\) would make it equal to zero and then you can exclude those values.
\(\begin{aligned} x^{2}+7 x+12 &=0 \\(x+4)(x+3) &=0 \\ x &=-4,-3 \end{aligned}\)
Domain: \(x \in(-\infty,-4) \cup(-4,-3) \cup(-3, \infty)\)
3. \(y=-4 \ln (3 x-9)+11\)
The argument must be strictly greater than 0 .
\(3 x-9>0\)
\(3 x>9\)
\(x>3\)
Domain: \(x \in(3, \infty)\)
What is the domain and range of the sine wave?
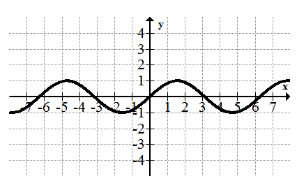
Domain: \(x \in(-\infty, \infty)\)
Range: \(y \in[-1,1]\)
Review
Convert the following descriptions of numbers into interval notation.
1. All positive numbers not including 0.
2. Every number between -1 and 1 including -1 but not 1.
3. Every number between 1 and 5 not including 2 or 3, but including 1 and 5.
4. Every number greater than 5, not including 5.
5. All real numbers except 1.
Translate the following inequalities into interval notation.
6. \(-4<x \leq 5\)
7. \(x>0\)
8. \(-\infty<x \leq 4\) or \(5<x<\infty\)
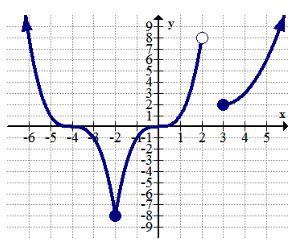
9.
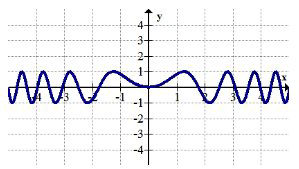
10.
Given the stated domain and range, draw a possible graph.
11. Domain: \(x \in[0, \infty)\) Range: \(y \in(-2,2]\)
12. Domain: \(x \in[-4,1) \cup(1, \infty)\) Range: \(y \in(-\infty, \infty)\)
13. Given the table, find the domain and range.
Find the domain for the following functions.
14. \(y=-3 \sqrt{x+4}-1\)
\(y=\frac{7}{x+6}-1\)
16. \(y=5 \ln \left(x^{2}-1\right)+4\)

