1.11: 1.11 Function Composition
- Page ID
- 11456
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Functions can be added, subtracted, multiplied and divided creating new functions and graphs that are complicated combinations of the various original functions. One important way to transform functions is through function composition. Function composition allows you to line up two or more functions that act on an input in tandem.
Is function composition essentially the same as multiplying the two functions together?
Composition of Functions
A common way to describe functions is a mapping from the domain space to the range space:
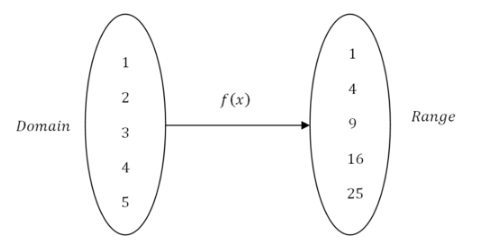
Function composition means that you have two or more functions and the range of the first function becomes the domain of the second function.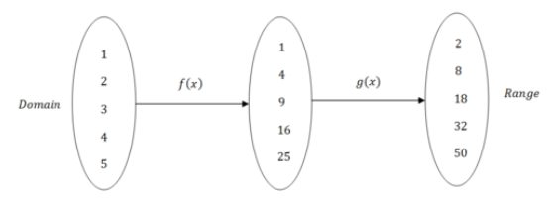
There are two notations used to describe function composition. In each case the order of the functions matters because arithmetically the outcomes will be different. Squaring a number and then doubling the result will be different from doubling a number and then squaring the result. In the diagram above, \(f(x)\) occurs first and \(g(x)\) occurs second. This can be written as:
\(g(f(x))\) or \((g \circ f)(x)\)
You should read this " \(g\) of \(f\) of \(x\)." In both cases notice that the \(f\) is closer to the
\(x\) and operates on the \(x\) values first.
Examples
Earlier, you were asked if function composition is the same as multiplying two functions together. Function composition is not the same as multiplying two functions together. With function composition there is an outside function and an inside function. Suppose the two functions were doubling and squaring. It is clear just by looking at the example input of the number 5 that 50 (squaring then doubling) is different from 100 (doubling then squaring). Both 50 and 100 are examples of function composition, while 250 (five doubled multiplied by five squared) is an example of the product of two separate functions happening simultaneously.
For the next two examples, use the functions below:
\(f(x)=x^{2}-1\)
\(h(x)=\frac{x-1}{x+5}\)
\(g(x)=3 e^{x}-x\)
\(j(x)=\sqrt{x+1}\)
Show \(f(h(x)) \neq h(f(x))\)
\(f(h(x))=f\left(\frac{x-1}{x+5}\right)=\left(\frac{x-1}{x+5}\right)^{2}-1\)
\(h(f(x))=h\left(x^{2}-1\right)=\frac{\left(x^{2}-1\right)-1}{\left(x^{2}-1\right)+5}=\frac{x^{2}-2}{x^{2}+4}\)
In order to truly show they are not equal it is best to find a specific counter example of a number where they differ. Sometimes algebraic expressions may look different, but are actually the same. You should notice that \(f(h(x))\) is undefined when \(x=-5\) because then there would be zero in the denominator. \(h(f(x))\) on the other hand is defined at \(x=-5 .\) since the two function compositions differ, you can conclude:
\(f(h(x)) \neq h(f(x))\)
What is \(f(j(h(g(x)))) ?\)
These functions are nested within the arguments of the other functions. Sometimes functions simplify significantly when composed together, as \(f\) and \(j\) do in this case. It makes sense to evaluate those two functions first together and keep them on the outside of the argument.
\(f(x)=x^{2}-1 ; h(x)=\frac{x-1}{x+5} ; g(x)=3 e^{x}-x ; j(x)=\sqrt{x+1}\)
\(f(j(y))=f(\sqrt{y+1})=(\sqrt{y+1})^{2}-1=y+1-1=y\)
Notice how the composition of \(f\) and \(j\) produced just the argument itself?
Thus,
\(\begin{aligned} f(j(h(g(x))))=h(g(x)) &=h\left(3 e^{x}-x\right) \\ &=\frac{\left(3 e^{x}-x\right)-1}{\left(3 e^{x}-x\right)+5} \\ &=\frac{3 e^{x}-x-1}{3 e^{x}-x+5} \end{aligned}\)
For the next two examples, use the graphs shown below:
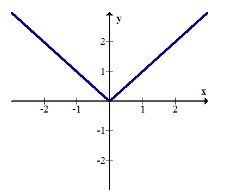
\(f(x)=|x|\)
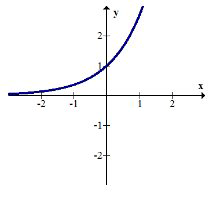
\(g(x)=e^{x}\)
\(h(x)=-x\)
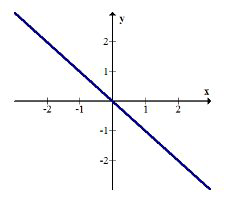
Compose \(g(f(x))\) and graph the result. Describe the transformation.
\(g(f(x))=g(|x|)=e^{|x|}\)
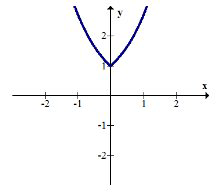
The positive portion of the exponential graph has been mirrored over the \(y\) axis and the negative portion of the exponential graph has been entirely truncated.
Compose \(h(g(x))\) and graph the result. Describe the transformation.
\(h(g(x))=h\left(e^{x}\right)=-e^{x}\)
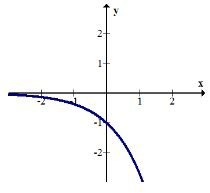
The exponential graph has been reflected over the \(x\) -axis.
Review
For questions 1-9, use the following three functions: \(f(x)=|x|, h(x)=-x, g(x)=(x-2)^{2}-3\)
1. Graph \(f(x), h(x)\) and \(g(x)\).
2. Find \(f(g(x))\) algebraically.
3. Graph \(f(g(x))\) and describe the transformation.
4. Find \(g(f(x))\) algebraically.
5. Graph \(g(f(x))\) and describe the transformation.
6. Find \(h(g(x))\) algebraically.
7. Graph \(h(g(x))\) and describe the transformation.
8. Find \(g(h(x))\) algebraically.
9. Graph \(g(h(x))\) and describe the transformation.
For 10-16, use the following three functions: \(j(x)=x^{2}, k(x)=|x|, m(x)=\sqrt{x}\)
10. Graph \(j(x), k(x)\) and \(m(x)\).
11. Find \(j(k(x))\) algebraically.
12. Graph \(j(k(x))\) and describe the transformation.
13. Find \(k(m(x))\) algebraically.
14. Graph \(k(m(x))\) and describe the transformation.
15. Find \(m(k(x))\) algebraically.
16. Graph \(m(k(x))\) and describe the transformation.