Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Home
Bookshelves
Mathematics
Precalculus
1: Functions and Graphs
1.3: 1.3 Point Notation and Function Notation

1.3: 1.3 Point Notation and Function Notation

Last updated

Feb 13, 2022
Save as PDF
- 1.2: 1.2 Graphical Transformations
- 1.4: 1.4 Domain and Range

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

When performing multiple transformations, it is very easy to make a small error. This is especially true when you try to do every step mentally. Point notation is a useful tool for concentrating your efforts on a single point and helps you to avoid making small mistakes.

What would $f(3 x)+7$ look like in point notation and why is it useful?

Using Function Notation and Point Notation

A transformation can be written in function notation and in point notation. Function notation is very common and practical because it allows you to graph any function using the same basic thought process it takes to graph a parabola in vertex form.

Another way to graph a function is to transform each point one at a time. This method works well when a table of $x, y$ values is available or easily identified from the graph.

Essentially, it takes each coordinate $(x, y)$ and assigns a new coordinate based on the transformation.

$(x, y) \longrightarrow($ new $x,$ new $y)$

This notation is called point notation. The new $y$ coordinate is straightforward and is directly from what takes place outside $f(x)$ because $f(x)$ is just another way to write $y$ . For example, $f(x) \rightarrow 2 f(x)-1$ would have a new $y$ coordinate of $2 y-1$ .

The new $x$ coordinate is trickier. It comes from undoing the operations that affect $x$ . For example, $f(x) \rightarrow f(2 x-1)$ would have a new $x$ coordinate of $\frac{x+1}{2}$

The function notation and point notation representations of the transformation "Horizontal shift right three units, vertical shift up 4 units" are

$f(x) \rightarrow f(x-3)+4$

$(x, y) \rightarrow(x+3, y+4)$

Notice that the operations with the $x$ are different.

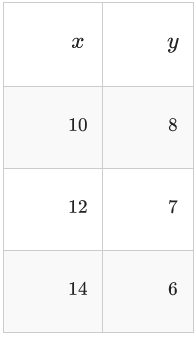
Apply the transformation above to the following table of points.

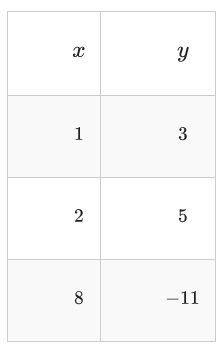
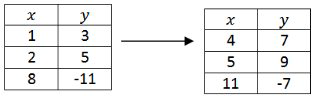
Notice that point notation greatly reduces the mental visualization required to keep all the transformations straight at once.

Examples

Example 1

Earlier, you were asked what the function $f(3 x)+7$ would be when written in point notation. When written in point notation, it would be written as $(x, y) \rightarrow\left(\frac{x}{3}, y+7\right) .$ This is useful because it becomes obvious that the $x$ values are all divided by three and the $y$ values all increase by 7 .

Example 2

Convert the following function in point notation to words and then function notation.

$(x, y) \rightarrow(3 x+1,-y+7)$

Horizontal stretch by a factor of 3 and then a horizontal shift right one unit. Vertical reflection over the $x$ axis and then a vertical shift 7 units up.

$f(x) \rightarrow-f\left(\frac{1}{3} x-\frac{1}{3}\right)+7$

Example 3

Convert the following function notation into words and then point notation. Finally, apply the transformation to three example points.

$f(x) \rightarrow-2 f(x-1)+4$

Vertical reflection across the $x$ axis. Vertical stretch by a factor of $2 .$ Vertical
shift 4 units. Horizontal shift right one unit.

$(x, y) \rightarrow(x+1,-2 y+4)$

Example 4

Convert the following function notation into point notation and apply it to the included table of points

$f(x) \rightarrow \frac{1}{4} f(-x-3)-1$

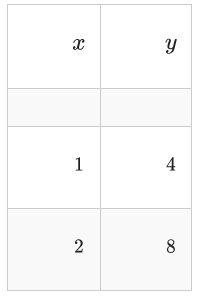
The $y$ component can be directly observed. For the $x$ component you need to undo the argument. $(x, y) \rightarrow\left(-x-3, \frac{1}{4} y-1\right)$

Example 5

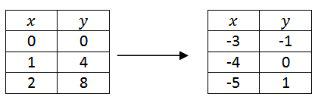
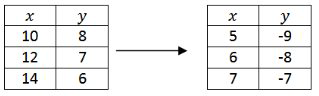
Convert the following point notation to words and to function notation and then apply the transformation to the included table of points.

$(x+3, y-1) \rightarrow(2 x+6,-y)$

This problem is different because it seems like there is a transformation
happening to the original left point. This is an added layer of challenge
because the transformation of interest is just the difference between the two
points. Notice that the $x$ coordinate has simply doubled and the $y$
coordinate has gotten bigger by one and turned negative. This problem can
be rewritten as:

$(x, y) \rightarrow(2 x,-(y+1))=(2 x,-y-1)$

$f(x) \rightarrow-f\left(\frac{x}{2}\right)-1$

Review

Convert the following function notation into words and then point notation. Finally, apply the transformation to three example points.

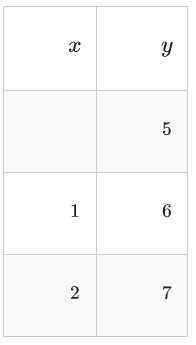
1. 9 $f(x) \rightarrow-\frac{1}{2} f(x+1)$
2. $g(x) \rightarrow 2 g(3 x)+2$
3. $h(x) \rightarrow-h(x-4)-3$
4. $j(x) \rightarrow 3 j(2 x-4)+1$
5. $k(x) \rightarrow-k(x-3)$

Convert the following functions in point notation to function notation.

6. $(x, y) \rightarrow\left(\frac{1}{2} x+3, y-4\right)$
7. $(x, y) \rightarrow(2 x+4,-y+1)$
8. $(x, y) \rightarrow(4 x, 3 y-5)$
9. $(2 x, y) \rightarrow(4 x,-y+1)$
10. $(x+1, y-2) \rightarrow(3 x+3,-y+3)$

Convert the following functions in function notation to point notation.

11. $f(x) \rightarrow 3 f(x-2)+1$
12. $g(x) \rightarrow-4 g(x-1)+3$
13. $h(x) \rightarrow \frac{1}{2} h(2 x+2)-5$
14. $j(x) \rightarrow 5 j\left(\frac{1}{2} x-2\right)-1$
15. $k(x) \rightarrow \frac{1}{4} k(2 x-4)$