2.4.6: Trig Functions as Algebra Expressions
- Page ID
- 14484
Relationships between the lengths of two sides of a triangle.
Trigonometry in Terms of Algebra
You are babysitting your little cousin while doing your homework. While working on your trig functions, your cousin asks you what you are doing. While trying to explain sine, cosine, and tangent, your cousin is very confused. She doesn't understand what you mean by those words, but really wants to understand what the functions mean. Can you define the trig functions in terms of the relationships of sides for your little cousin?
Solving Trigonometric Functions
All of the trigonometric functions can be rewritten in terms of only \(x\), when using one of the inverse trigonometric functions.
Starting with tangent, we draw a triangle where the opposite side (from \(\theta \)) is defined as \(x\) and the adjacent side is 1. The hypotenuse, from the Pythagorean Theorem would be \(\sqrt{x^2+1}\). Substituting \(\tan^{-1} x\) for \(\theta \), we get:
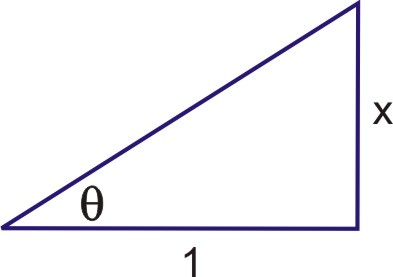
\(\begin{aligned}
\tan \theta &=\dfrac{x}{1} \\
\tan \theta &=x \quad \text { hypotenuse }=\sqrt{x^{2}+1} \\
\theta &=\tan ^{-1} x
\end{aligned}\)
\(\begin{array}{ll}
\sin \left(\tan ^{-1} x\right)=\sin \theta=\dfrac{x}{\sqrt{x^{2}+1}} & \csc \left(\tan ^{-1} x\right)=\csc \theta=\dfrac{\sqrt{x^{2}+1}}{x} \\
\cos \left(\tan ^{-1} x\right)=\cos \theta=\dfrac{1}{\sqrt{x^{2}+1}} & \sec \left(\tan ^{-1} x\right)=\sec \theta=\sqrt{x^{2}+1} \\
\tan \left(\tan ^{-1} x\right)=\tan \theta=x & \cot \left(\tan ^{-1} x\right)=\cot \theta=\dfrac{1}{x}
\end{array}\)
Simplifying Trigonometric Functions
1. Find \(\sin(\tan^{-1}3x)\).
Instead of using \(x\) in the ratios above, use \(3x\).
\(\sin(\tan^{-1}3x)=\sin \theta =\dfrac{3x}{\sqrt{(3x)^2+1}}=\dfrac{3x}{\sqrt{9x^2+1}}\)
2. Find \(\sec^2(\tan^{-1}x)\).
This problem might be better written as \([\sec(\tan^{-1}x)]^2\). Therefore, all you need to do is square the ratio above.
\([\sec(\tan^{-1}x)]^2=(\sqrt{x^2+1})^2=x^2+1\)
You can also write the all of the trig functions in terms of arcsine and arccosine. However, for each inverse function, there is a different triangle. You will derive these formulas in the exercise for this section.
3. Find \(\csc^3(\tan^{-1}4x)\).
This problem is similar to #1 and #2 above. First, use \(4x\) instead of \(x\) in the ratios above. Second, the \(csc^3\) is the same as taking the csc function and cubing it.
\([\csc(\tan^{-1}4x)]^3=\left(\dfrac{\sqrt{(4x)^2+1}}{4x}\right)^3=\dfrac{(16x^2+1)^{\frac{3}{2}}}{64x^3}\)
Earlier, you were asked if you can define the trig functions in terms of the relationship of sides.
Solution
As it turns out, it's very easy to explain trig functions in terms of ratios. If you look at the unit circle
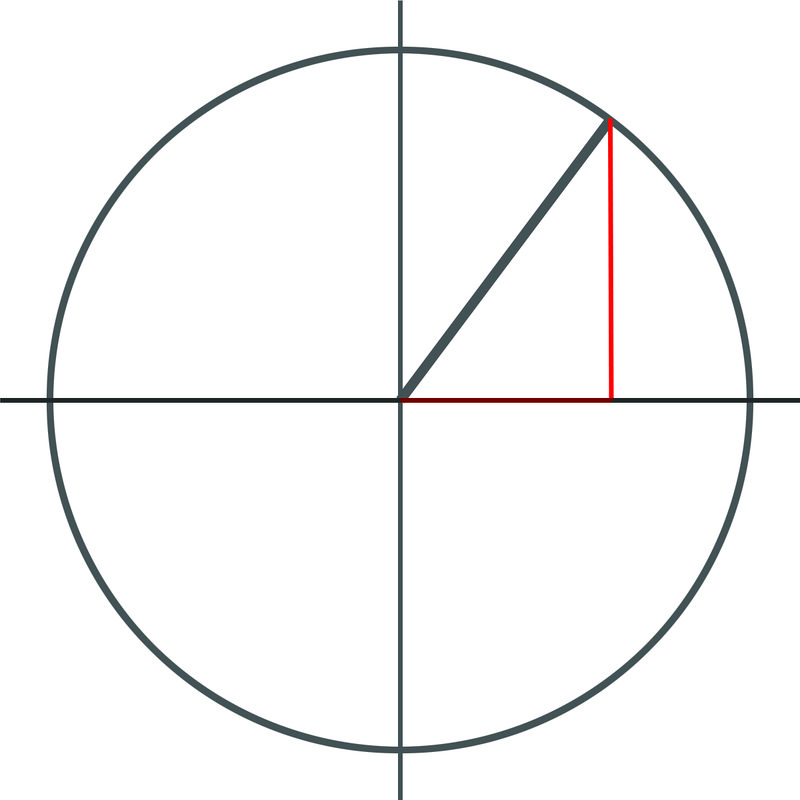
you can see that each trig function can be represented as a ratio of two sides. The value of any trig function can be represented as the length of one of the sides of the triangle (shown with two red sides and the black hypotenuse) divided by the length of one of the other sides. In fact, you should explain to your cousin, the words like "sine", "cosine", and "tangent" are just conveniences in this case to describe relationships that keep coming up over and over again. It would be possible to just describe the trig functions in terms of relationships of one side to another, if you'd like.
Using the sides of a triangle made on the unit circle, if the side opposite the angle is called "\(x\)":
\(\begin{aligned}
\sin &=\dfrac{\text { opposite }}{\text { hypotenuse }}=\dfrac{x}{\sqrt{x^{2}+1}} \\
\cos &=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{1}{\sqrt{x^{2}+1}} \\
\tan &=\dfrac{\text { opposite }}{\text { adjacent }}=\dfrac{x}{1}
\end{aligned}\)
So as you can see, since trig functions are really just relationships between sides, it is possible to work with them in whatever form you want; either in terms of the usual "sine", "cosine" and "tangent", or in terms of algebra.
Express \(\cos^2(\tan^{−1} x)\) as an algebraic expression involving no trigonometric functions.
Solution
\(\dfrac{1}{x^2+1}\)
Express \(\cot(\tan^{−1}x^2)\) as an algebraic expression involving no trigonometric functions.
Solution
\(\dfrac{1}{x^2}\)
To find trigonometric functions in terms of sine inverse, use the following triangle.
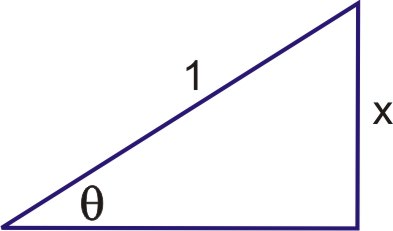
Solution
Determine the sine, cosine and tangent in terms of arcsine. Find \(\tan(\sin^{−1}2x^3)\).
The adjacent side to \(\theta \) is \(\sqrt{1−x^2}\), so the three trig functions are:
\(\begin{aligned}
\sin \left(\sin ^{-1} x\right)&=\sin \theta=x \\
\cos \left(\sin ^{-1} x\right)&=\cos \theta=\sqrt{1-x^{2}} \\
\tan \left(\sin ^{-1} x\right)&=\tan \theta=\dfrac{x}{\sqrt{1-x^{2}}} \\
\tan \left(\sin ^{-1}\left(2 x^{3}\right)\right)&=\dfrac{2 x^{3}}{\sqrt{1-\left(2 x^{3}\right)^{2}}}=\dfrac{2 x^{3}}{\sqrt{1-4 x^{6}}}
\end{aligned}\)
Review
Rewrite each expression as an algebraic expression involving no trigonometric functions.
- \(\sin(\tan^{-1}5x)\)
- \(\cos(\tan^{-1}2x^2)\)
- \(\cot(\tan^{-1}3x^2)\)
- \(\sin(\cos^{-1}x)\)
- \(\sin(\cos^{-1}3x)\)
- \(\cos(\sin^{-1}2x^2)\)
- \(\csc(\cos^{-1}x)\)
- \(\sec(\sin^{-1}x)\)
- \(\cos2(\tan^{-1}3x^2)\)
- \(\sin(\sec^{-1}x)\)
- \(\cos(\csc−1x)\)
- \(\sin(\tan^{-1}2x^3)\)
- \(\cos(\sin^{-1}3x)\)
- \(\sin(\sec^{-1}x)\)
- \(\cos(\cot^{-1}x)\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.9.
Vocabulary
| Term | Definition |
|---|---|
| Trigonometric Function | A trigonometric function is a function of an angle that describes the relationship between two sides of a right triangle. Examples of trigonometric functions are sine, cosine, and tangent. |
| Trigonometric Functions | A trigonometric function is a function of an angle that describes the relationship between two sides of a right triangle. Examples of trigonometric functions are sine, cosine, and tangent. |
Additional Resources
Video: Unit Circle Definition of Trig Functions
Practice: Trig Functions as Algebra Expressions

