4.27: The Pythagorean Theorem
- Page ID
- 4958
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Square of the hypotenuse equals the sum of the squares of the legs in right triangles.
The two shorter sides of a right triangle (the sides that form the right angle) are the legs and the longer side (the side opposite the right angle) is the hypotenuse. For the Pythagorean Theorem, the legs are “\(a\)” and “\(b\)” and the hypotenuse is “\(c\)”.
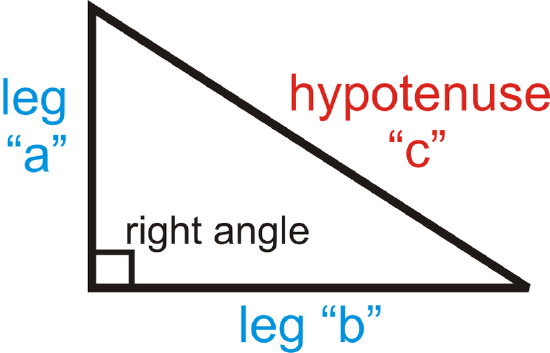
Pythagorean Theorem: Given a right triangle with legs of lengths a and b and a hypotenuse of length \(c\), \(a^2+b^2=c^2\).
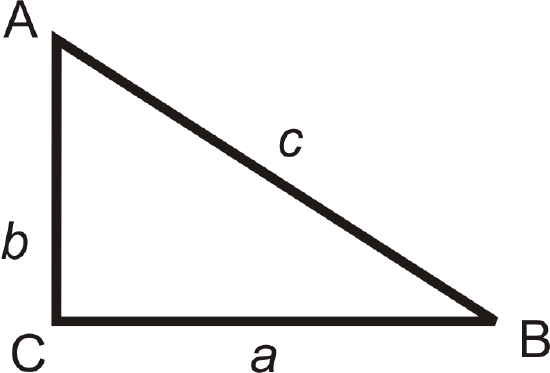
The converse of the Pythagorean Theorem is also true. It allows you to prove that a triangle is a right triangle even if you do not know its angle measures.
Pythagorean Theorem Converse: If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
If \(a^2+b^2=c^2\), then \(\Delta ABC\) is a right triangle.
Pythagorean Triples
A combination of three numbers that makes the Pythagorean Theorem true is called a Pythagorean triple. Each set of numbers below is a Pythagorean triple.
\(3,4,5 \qquad 5,12,13\qquad 7,24,25\qquad 8,15,17\qquad 9,12,15\qquad 10,24,26\)
Any multiple of a Pythagorean triple is also considered a Pythagorean triple. Multiplying 3, 4, 5 by 2 gives 6, 8, 10, which is another triple. To see if a set of numbers makes a Pythagorean triple, plug them into the Pythagorean Theorem.
What if you were told that a triangle had side lengths of 5, 12, and 13? How could you determine if the triangle were a right one?
Example \(\PageIndex{1}\)
What is the diagonal of a rectangle with sides 10 and 16?
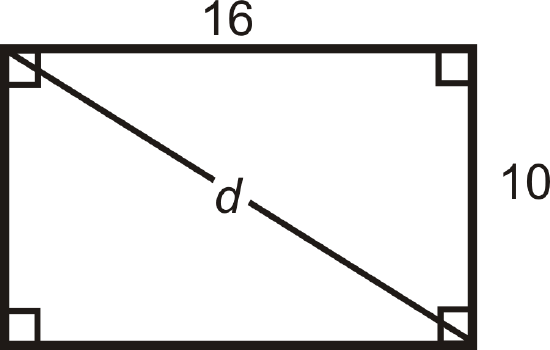
Solution
For any square and rectangle, you can use the Pythagorean Theorem to find the length of a diagonal. Plug in the sides to find \(d\).
\(\begin{align*} 10^2+16^2=d^2 \\ 100+256=d^2 \\ 356&=d^2 \\ d&=\sqrt{356}=2\sqrt{89}\approx 18.87 \end{align*}\)
Example \(\PageIndex{2}\)
Do 6, 7, and 8 make the sides of a right triangle?
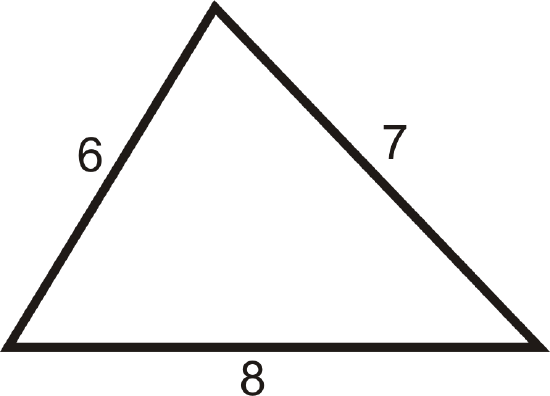
Solution
Plug the three numbers into the Pythagorean Theorem. Remember that the largest length will always be the hypotenuse, c. If \(6^2+7^2=8^2\), then they are the sides of a right triangle.
\(\begin{align*} 6^2+7^2&=36+49=85& \\ 8^2&=64&\qquad 85 \neq 64,\: so\: the \:lengths \:are \:not \:the \:sides \:of \:a \:right \:triangle.\end{align*}\)
Example \(\PageIndex{3}\)
Find the length of the hypotenuse.
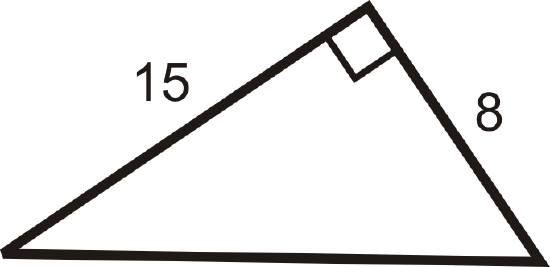
Solution
Use the Pythagorean Theorem. Set \(a=8\) and \(b=15\). Solve for \(c\).
\(\begin{align*} 8^2+152&=c^2 \\ 64+225&=c^2 \\ 289&=c^2 \qquad Take\: the \:square \:root \:of \:both \:sides. \\ 172&=c\end{align*}\)
Example \(\PageIndex{4}\)
Is 20, 21, 29 a Pythagorean triple?
Solution
If \(20^2+21^2=29^2\), then the set is a Pythagorean triple.
\(\begin{align*} 20^2+21^2&=400+441=841 \\ 29^2&=841 \end{align*}\)
Therefore, 20, 21, and 29 is a Pythagorean triple.
Example \(\PageIndex{5}\)
Determine if the triangles below are right triangles.
Check to see if the three lengths satisfy the Pythagorean Theorem. Let the longest side represent c.
Solution
-
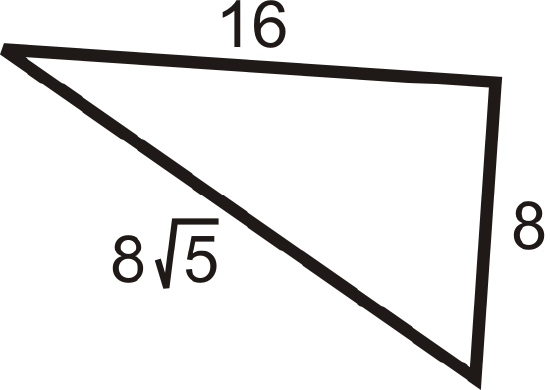
Figure \(\PageIndex{6}\)
\(\begin{align*} a^2+b^2&=c^2 \\ 82+162 &\stackrel{?}{=}(8\sqrt{5})2 \\ 64+256 &\stackrel{?}{=}64\cdot 5 \\ 320&=320\qquad Yes\end{align*} \)
-
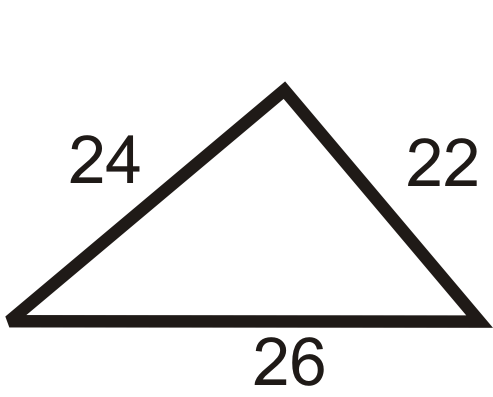
Figure \(\PageIndex{7}\)
\(\begin{align*} a^2+b^2&=c^2 \\ 22^2+24^2&\stackrel{?}{=}262 \\ 484+576 &\stackrel{?}{=}676 \\ 1060 &\neq 676\qquad No\end{align*}\)
Review
Find the length of the missing side. Simplify all radicals.
-
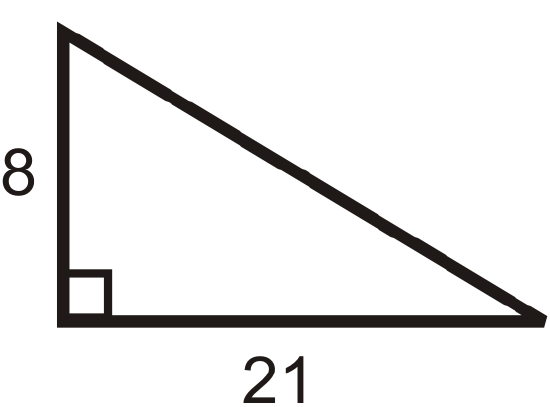
Figure \(\PageIndex{8}\) -
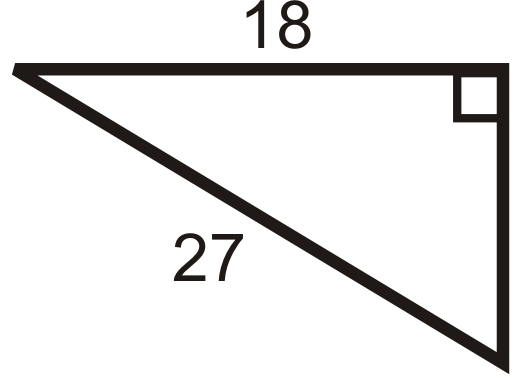
Figure \(\PageIndex{9}\) -
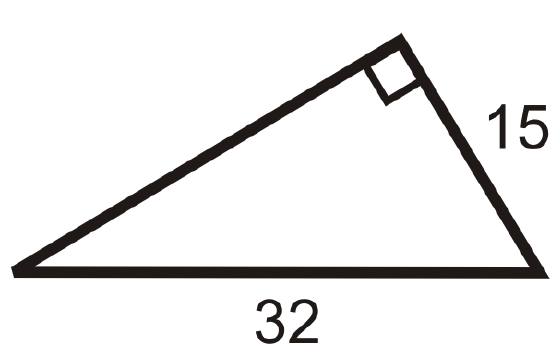
Figure \(\PageIndex{10}\) -
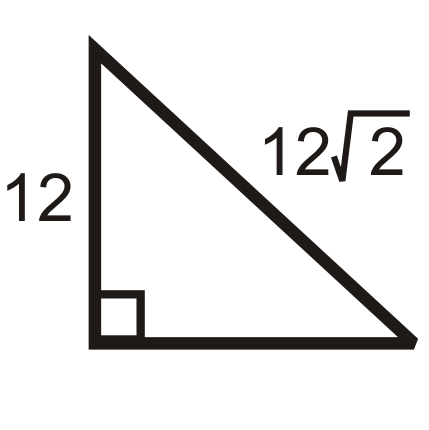
Figure \(\PageIndex{11}\) -
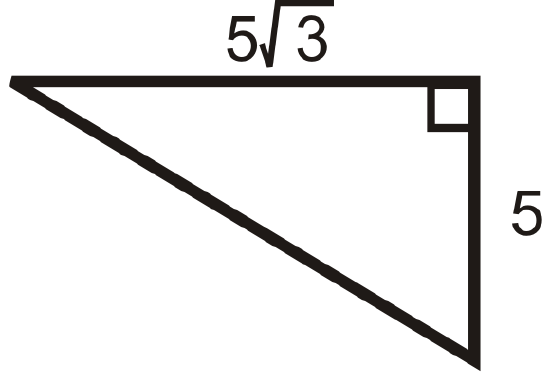
Figure \(\PageIndex{12}\) -
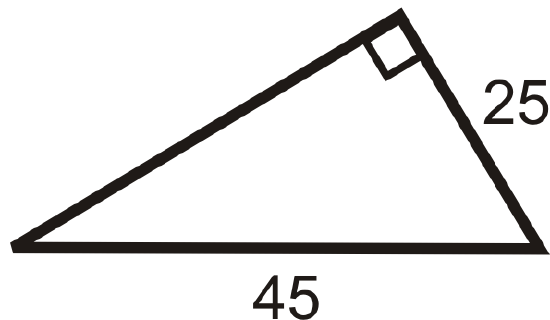
Figure \(\PageIndex{13}\) - If the legs of a right triangle are 10 and 24, then the hypotenuse is __________.
- If the sides of a rectangle are 12 and 15, then the diagonal is _____________.
- If the sides of a square are 16, then the diagonal is ____________.
- If the sides of a square are 9, then the diagonal is _____________.
Determine if the following sets of numbers are Pythagorean Triples.
- 12, 35, 37
- 9, 17, 18
- 10, 15, 21
- 11, 60, 61
- 15, 20, 25
- 18, 73, 75
Determine if the following lengths make a right triangle.
- 7, 24, 25
- \(\sqrt{5},2\sqrt{10},3\sqrt{5}\)
- \(2\sqrt{3},\sqrt{6},8\)
- 15, 20, 25
- 20, 25, 30
- \(8\sqrt{3},6,2\sqrt{39}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.2.
Vocabulary
| Term | Definition |
|---|---|
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle. |
| Pythagorean triple | A combination of three numbers that makes the Pythagorean Theorem true. |
| Circle | A circle is the set of all points at a specific distance from a given point in two dimensions. |
| Conic | Conic sections are those curves that can be created by the intersection of a double cone and a plane. They include circles, ellipses, parabolas, and hyperbolas. |
| degenerate conic | A degenerate conic is a conic that does not have the usual properties of a conic section. Since some of the coefficients of the general conic equation are zero, the basic shape of the conic is merely a point, a line or a pair of intersecting lines. |
| Ellipse | Ellipses are conic sections that look like elongated circles. An ellipse represents all locations in two dimensions that are the same distance from two specified points called foci. |
| hyperbola | A hyperbola is a conic section formed when the cutting plane intersects both sides of the cone, resulting in two infinite “U”-shaped curves. |
| Hypotenuse | The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
| Parabola | A parabola is the characteristic shape of a quadratic function graph, resembling a "U". |
| Pythagorean number triple | A Pythagorean number triple is a set of three whole numbers a,b and c that satisfy the Pythagorean Theorem, \(a^2+b^2=c^2\). |
| Right Triangle | A right triangle is a triangle with one 90 degree angle. |
Additional Resources
Interactive Element
Video: Using The Pythagorean Theorem Principles - Basic
Activities: Pythagorean Theorem and Pythagorean Triples Discussion Questions
Study Aids: Pythagorean Theorem Study Guide
Practice: The Pythagorean Theorem
Real World: Pythagoras TV

