4.6: Area and Perimeter of Triangles
- Page ID
- 2176
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Area is half the base times the height while the perimeter is the sum of the sides.
The formula for the area of a triangle is half the area of a parallelogram.
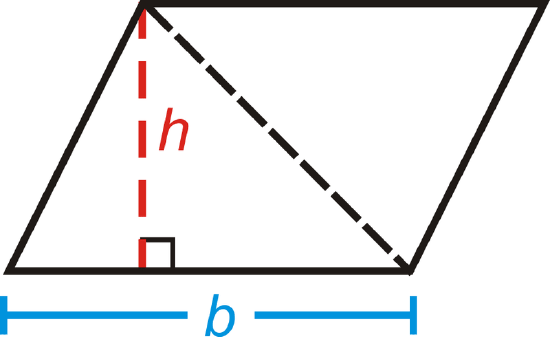
Area of a Triangle: \(A=\dfrac{1}{2} bh\) or \(A=\dfrac{bh}{2}\).
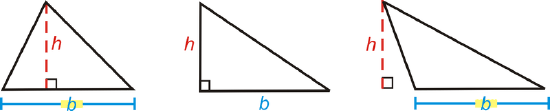
What if you were given a triangle and the size of its base and height? How could you find the total distance around the triangle and the amount of space it takes up?
For Examples 1 and 2, use the following triangle.
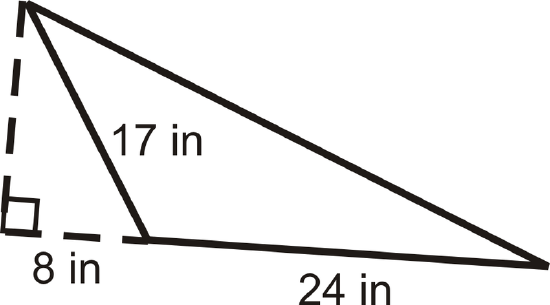
Example \(\PageIndex{1}\)
Find the height of the triangle.
Solution
Use the Pythagorean Theorem to find the height.
\(\begin{align*} 8^2+h^2 &=17^2 \\ h^2 &=225\\ h &=15 in \end{align*} \)
Example \(\PageIndex{2}\)
Find the perimeter.
Solution
We need to find the hypotenuse. Use the Pythagorean Theorem again.
\(\begin{align*} (8+24)^2+15^2 &=h^2 \\ h^2 &=1249 \\ h &\approx 35.3 in \end{align*}\)
The perimeter is \(24+35.3+17\approx 76.3\: in\).
Example \(\PageIndex{3}\)
Find the area of the triangle.
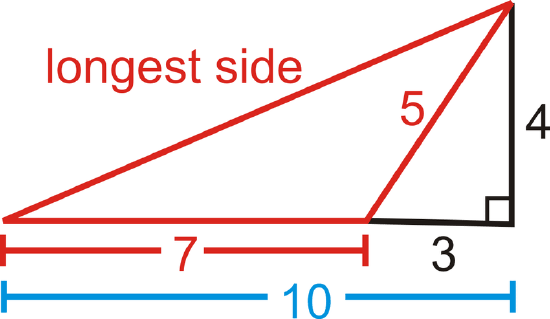
Solution
To find the area, we need to find the height of the triangle. We are given two sides of the small right triangle, where the hypotenuse is also the short side of the obtuse triangle.
\(\begin{align*} 3^2+h^2&=5^2 \\ 9+h^2&=25 \\ h^2&=16 \\h &=4 \\ A&=\dfrac{1}{2}(4)(7)=14 \: units^2 \end{align*}\)
Example \(\PageIndex{4}\)
Find the perimeter of the triangle in Example 3.
Solution
To find the perimeter, we need to find the longest side of the obtuse triangle. If we used the black lines in the picture, we would see that the longest side is also the hypotenuse of the right triangle with legs 4 and 10.
\(\begin{align*} 4^2+10^2&=c^2 \\ 16+100&=c^2 \\ c &=\sqrt{116}\approx 10.77 \end{align*} \)
The perimeter is \(7+5+10.77\approx 22.77\) units
Example \(\PageIndex{5}\)
Find the area of a triangle with base of length \(28 \: cm\) and height of \(15\: cm\).
Solution
The area is \(dfrac{1}{2}(28)(15)=210\: cm^2\).
Review
Use the triangle to answer the following questions.
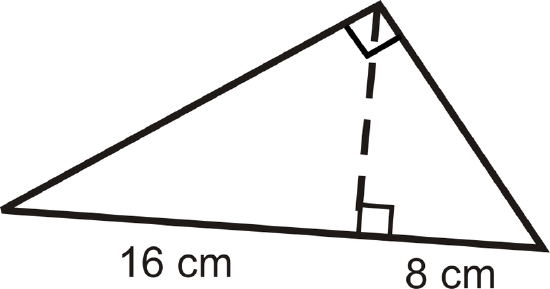
- Find the height of the triangle by using the geometric mean.
- Find the perimeter.
- Find the area.
Find the area of the following shape.
-
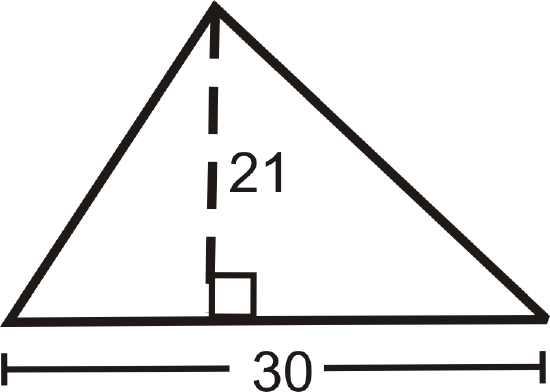
Figure \(\PageIndex{6}\) - What is the height of a triangle with area \(144\: m^2\) and a base of \(24\: m\)?
In questions 6-11 we are going to derive a formula for the area of an equilateral triangle.
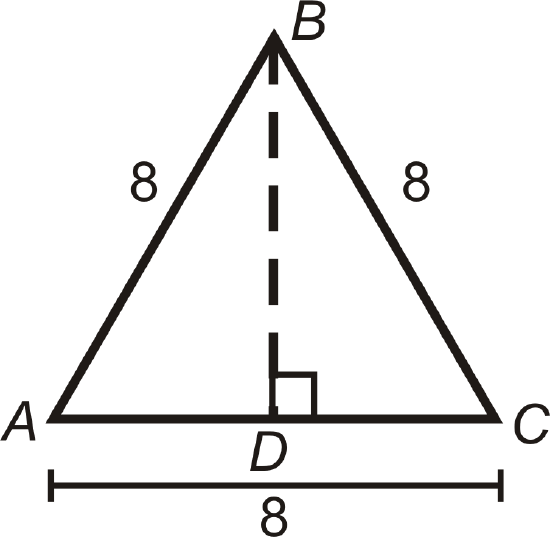
- What kind of triangle is \(\Delta ABD\)? Find \(AD\) and \(BD\).
- Find the area of \(\Delta ABC\).
- If each side is \(x\), what is \(AD\) and \(BD\)?
- If each side is \(x\), find the area of \(\Delta ABC\).
- Using your formula from #9, find the area of an equilateral triangle with 12 inch sides.
- Using your formula from #9, find the area of an equilateral triangle with 5 inch sides.
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.3.
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Perimeter | Perimeter is the distance around a two-dimensional figure. |
| Perpendicular | Perpendicular lines are lines that intersect at a 90∘ angle. The product of the slopes of two perpendicular lines is -1. |
| Right Angle | A right angle is an angle equal to 90 degrees. |
| Right Triangle | A right triangle is a triangle with one 90 degree angle. |
| Area of a Parallelogram | The area of a parallelogram is equal to the base multiplied by the height: \(A = bh\). The height of a parallelogram is always perpendicular to the base (the sides are not the height). |
| Area of a Triangle | The area of a triangle is half the area of a parallelogram. Hence the formula: \(A=\dfrac{1}{2} bh\) or \(A=\dfrac{bh}{2}\). |
Additional Resources
Interactive Element
Video: Area of a Triangle (Whole Numbers)
Activities: Area and Perimeter of Triangles Discussion Questions
Study Aids: Triangles and Quadrilaterals Study Guide
Practice: Area and Perimeter of Triangles
Real World: Perimeter

