4.4: Isosceles Triangles
- Page ID
- 2173
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Properties of triangles with two equal sides/angles.
An isosceles triangle is a triangle that has at least two congruent sides. The congruent sides of the isosceles triangle are called the legs. The other side is called the base. The angles between the base and the legs are called base angles. The angle made by the two legs is called the vertex angle. One of the important properties of isosceles triangles is that their base angles are always congruent. This is called the Base Angles Theorem.
For \(\DeltaDEF, if \(\overline{DE}\cong \overline{EF}\), then \(\angle D\cong \angle F\).
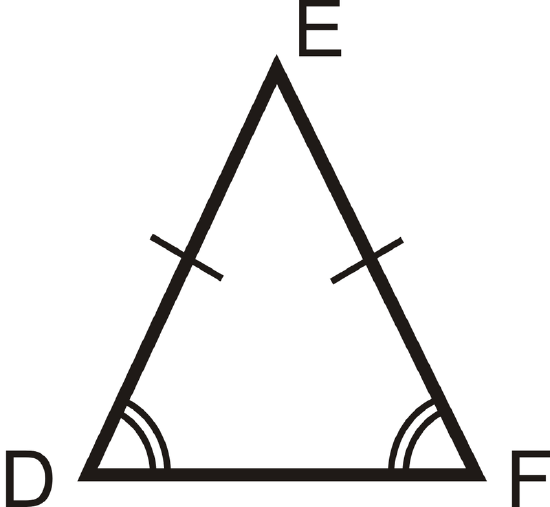
Another important property of isosceles triangles is that the angle bisector of the vertex angle is also the perpendicular bisector of the base. This is called the Isosceles Triangle Theorem. (Note this is ONLY true of the vertex angle.) The converses of the Base Angles Theorem and the Isosceles Triangle Theorem are both true as well.
Base Angles Theorem Converse: If two angles in a triangle are congruent, then the sides opposite those angles are also congruent. So for \(\Delta DEF\), if \(\angle D\cong \angle F\), then \(\overline{DE}\cong \overline{EF}\).

Isosceles Triangle Theorem Converse: The perpendicular bisector of the base of an isosceles triangle is also the angle bisector of the vertex angle. So for isosceles \(\DeltaDEF\), if \(\overline{EG}\perp \overline{DF}\) and \(\overline{DG}\cong \overline{GF}\), then \(\angle DEG\cong \angle FEG\).
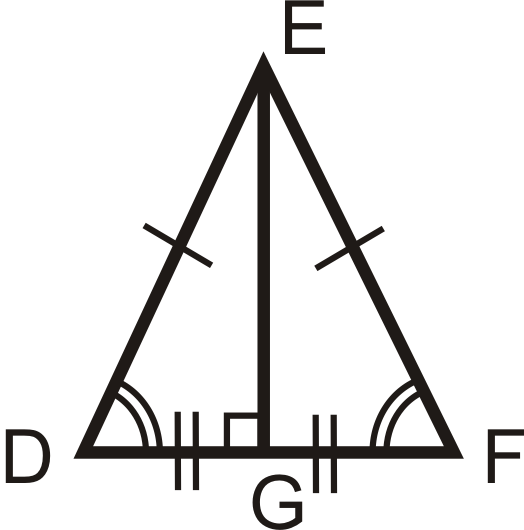
What if you were presented with an isosceles triangle and told that its base angles measure \(x^{\circ}\) and \(y^{\circ}\)? What could you conclude about \( x\)and \(y\)?
Example \(\PageIndex{1}\)
Find the value of \( x\) and the measure of each angle.
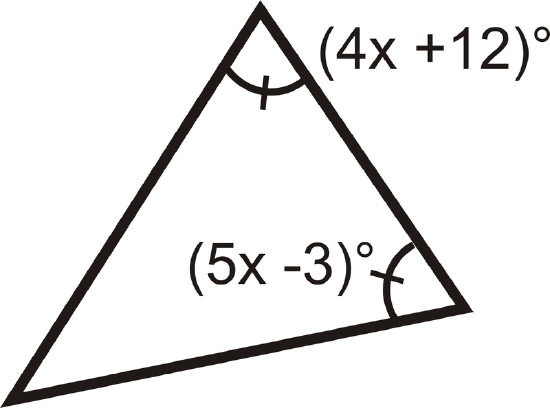
Solution
The two angles are equal, so set them equal to each other and solve for \(x\).
\(\begin{align*} (4x+12)^{\circ}&=(5x−3)^{\circ} \\ 15&=x\end{align*} \)
Substitute x=15; the base angles are \([4(15)+12]^{\circ}\), or 72^{\circ}\). The vertex angle is \(180^{\circ}−72^{\circ}−72^{\circ}=36^{\circ}\).
Example \(\PageIndex{2}\)
True or false: Base angles of an isosceles triangle can be right angles.
Solution
This statement is false. Because the base angles of an isosceles triangle are congruent, if one base angle is a right angle then both base angles must be right angles. It is impossible to have a triangle with two right (\(90^{\circ}\)) angles. The Triangle Sum Theorem states that the sum of the three angles in a triangle is \(180^{\circ}\). If two of the angles in a triangle are right angles, then the third angle must be \(0^{\circ}\) and the shape is no longer a triangle.
Example \(\PageIndex{3}\)
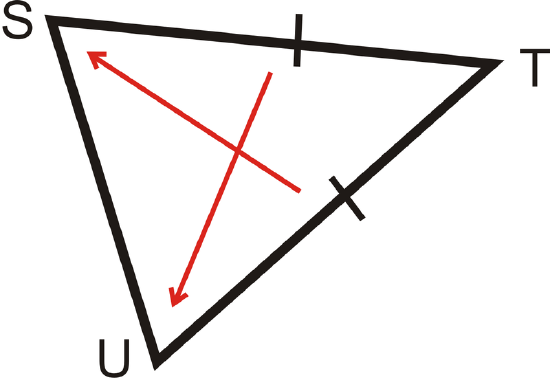
Which two angles are congruent?
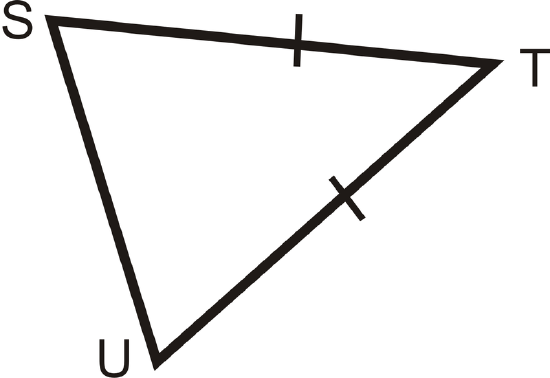
Solution
This is an isosceles triangle. The congruent angles are opposite the congruent sides. From the arrows we see that \(\angle S\cong \angle U\).
Example \(\PageIndex{4}\)
If an isosceles triangle has base angles with measures of \(47^{\circ}\), what is the measure of the vertex angle?
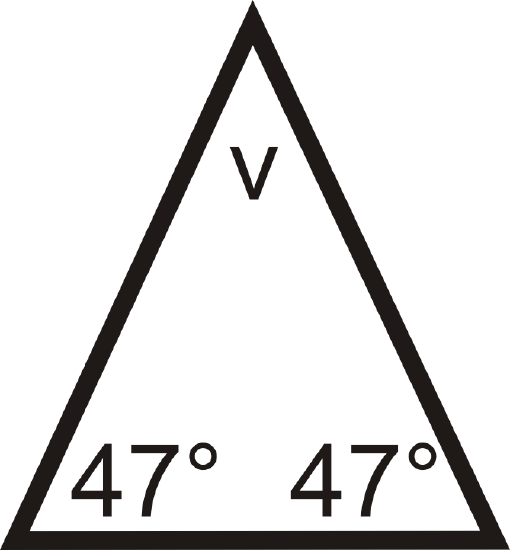
Solution
Draw a picture and set up an equation to solve for the vertex angle, \(v\). Remember that the three angles in a triangle always add up to \(180^{\circ}\).
\(\begin{align*} 47^{\circ}+47^{\circ}+v &=180^{\circ} \\ v &=180^{\circ}−47^{\circ}−47^{\circ} \\ v =86^{\circ} \end{align}\)
Example \(\PageIndex{5}\)
If an isosceles triangle has a vertex angle with a measure of \(116^{\circ}\), what is the measure of each base angle?
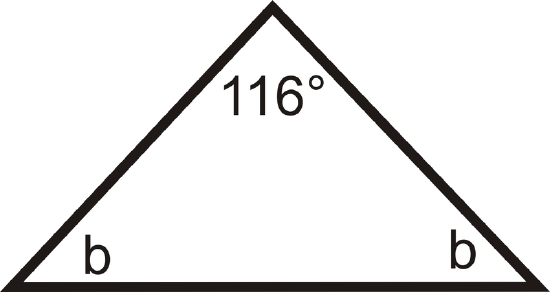
Solution
Draw a picture and set up and equation to solve for the base angles, \(b\).
\(\begin{align*} 116^{\circ}+b+b&=180^{\circ} \\ 2b&=64^{\circ} \\ b &=32^{\circ}\end{align*}\)
Review
Find the measures of \( x\)and/or \(y\).
-
Figure \(\PageIndex{9}\) -
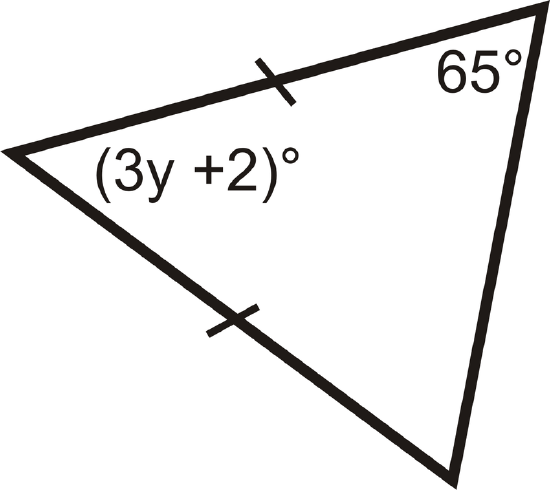
Figure \(\PageIndex{10}\) -
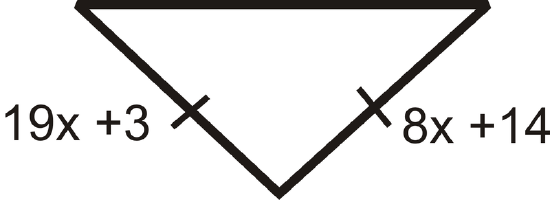
Figure \(\PageIndex{11}\) -
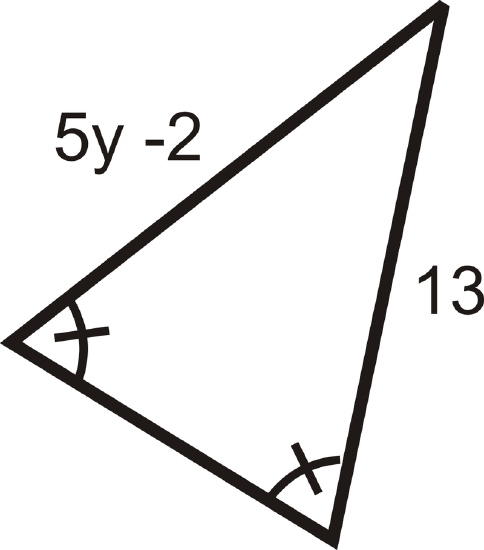
Figure \(\PageIndex{12}\) -
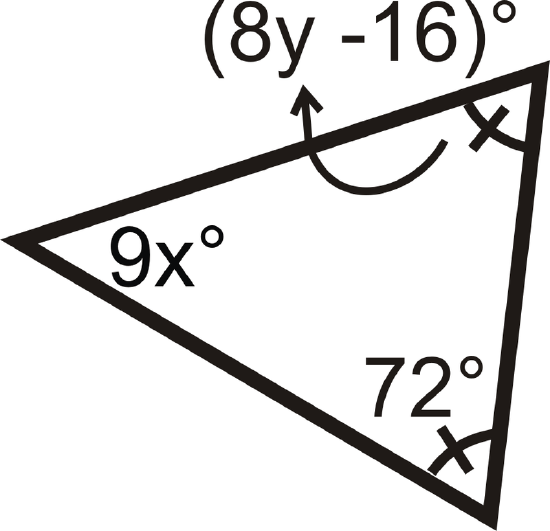
Figure \(\PageIndex{13}\)
Determine if the following statements are true or false.
- Base angles of an isosceles triangle are congruent.
- Base angles of an isosceles triangle are complementary.
- Base angles of an isosceles triangle can be equal to the vertex angle.
- Base angles of an isosceles triangle are acute.
Fill in the proofs below.
- Given: Isosceles \(\DeltaCIS\), with base angles \(\angle C\) and \(\angle S\). \overline{IO}\) is the angle bisector of \(\angle CIS\) Prove: \(\overline{IO}\) is the perpendicular bisector of \(\overline{CS}\)
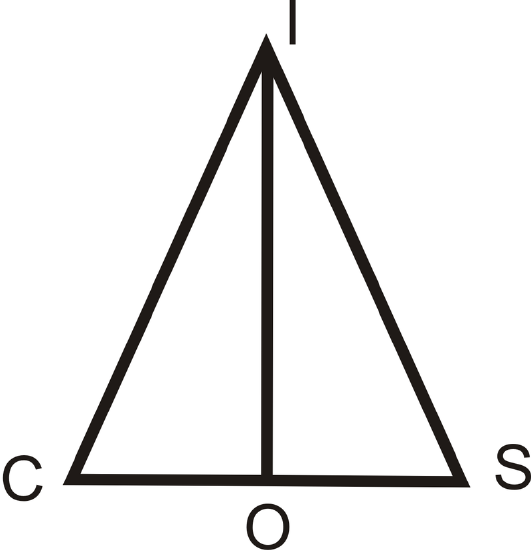
| Statement | Reason |
|---|---|
| 1. | 1. Given |
| 2. | 2. Base Angles Theorem |
| 3. \(\angle CIO\cong \angle SIO\) | 3. |
| 4. | 4. Reflexive \(PoC\) |
| 5. \(\DeltaCIO\cong \DeltaSIO\) | 5. |
| 6. \(\overline{CO}\cong \overline{OS}\) | 6. |
| 7. | 7. \(CPCTC\) |
| 8. \(\angle IOC\) and \(\angle IOS\) are supplementary | 8. |
| 9. | 9. Congruent Supplements Theorem |
| 10. \(\overline{IO}\) is the perpendicular bisector of \(\overline{CS}\) | 10. |
- Given: Isosceles \(\DeltaICS\) with \(\angle C\) and \(\angle S\). \(\overline{IO}\) is the perpendicular bisector of \(\overline{CS}\) Prove: \(\overline{IO}\) is the angle bisector of \(\angle CIS\)

| Statement | Reason |
|---|---|
| 1. | 1. |
| 2. \(\angle C\cong \angle S\) | 2. |
| 3. \(CO\overline{AB}\cong OS\overline{AB}\) | 3. |
| 4. \(m\angle IOC=m\angle IOS=90^{\circ}\) | 4. |
| 5. | 5. |
| 6. | 6. \(CPCTC\) |
| 7. \(\overline{IO}\) is the angle bisector of \(\angle CIS\) | 7. |
On the x−y plane, plot the coordinates and determine if the given three points make a scalene or isosceles triangle.
- \((-2, 1), (1, -2), (-5, -2)\)
- \((-2, 5), (2, 4), (0, -1)\)
- \((6, 9), (12, 3), (3, -6)\)
- \((-10, -5), (-8, 5), (2, 3)\)
- \((-1, 2), (7, 2), (3, 9)\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.10.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Base | The side of a triangle parallel with the bottom edge of the paper or screen is commonly called the base. The base of an isosceles triangle is the non-congruent side in the triangle. |
| Base Angles | The base angles of an isosceles triangle are the angles formed by the base and one leg of the triangle. |
| Base Angles Theorem Converse | The base angles theorem converse states if two angles in a triangle are congruent, then the sides opposite those angles are also congruent. |
| Isosceles Triangle Theorem | The Isosceles Triangle Theorem states that the perpendicular bisector of the base of an isosceles triangle is also the angle bisector of the vertex angle. |
| Triangle Sum Theorem | The Triangle Sum Theorem states that the three interior angles of any triangle add up to 180 degrees. |
| Vertical Angles | Vertical angles are a pair of opposite angles created by intersecting lines. |
Additional Resources
Interactive Element
Video: Isosceles Triangles Principles - Basic
Activities: Isosceles Triangles Discussion Questions
Study Aids: Triangle Relationships Study Guide
Practice: Isosceles Triangles
Real World: Triangles in the Sky

