4.3: Classify Triangles by Side Measurement
- Page ID
- 2177
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Classify triangles as scalene, isosoles or equalateral by identifying the number of equal sides.
Triangle Classification by Side Lengths
Tasha goes sailing with her father on her father's old boat. The sail looks like a triangle. All of the sides of the sail are different lengths. Tasha wants to classify the triangle but she isn't sure how to name it. Given the side lengths of the triangle, how can Tasha classify the triangle?
In this concept, you will learn how to classify triangles by their side lengths.
Classifying Triangles by Side Lengths
You can use the lengths of the sides to help you classify triangles.
Let’s look at how to classify triangles according to side length.
An equilateral triangle has side lengths that are the same. Here is an example.
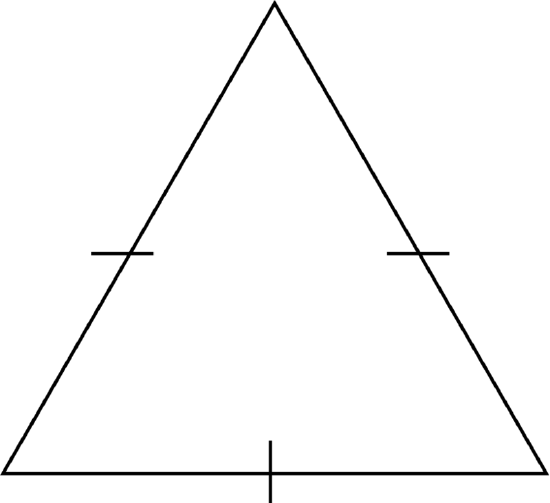
These little lines let you know that the side lengths are the same. Sometimes you will see these and sometimes you won’t. You may have to figure it out on your own or by measuring with a ruler.
A scalene triangle is a triangle where the lengths of all three sides are different. Here is an example of a scalene triangle.
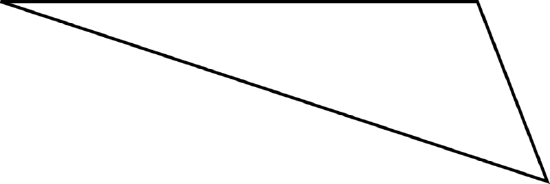
You can see that all three sides of the triangle are different lengths.
An isosceles triangle has two side lengths that are the same and one side length that is different. Here is an example of an isosceles triangle.
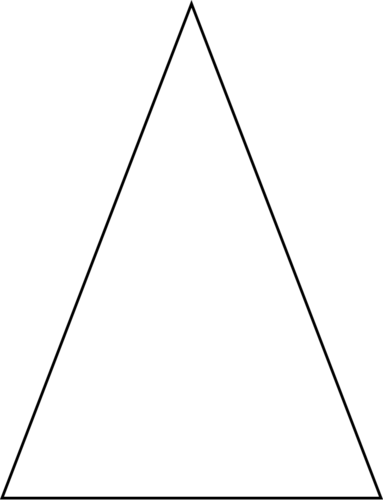Figure \(\PageIndex{4}\)Example \(\PageIndex{1}\)
Earlier, you were given a problem about Tasha and her sail.
Her sail is shaped like a triangle with different side lengths. What classification should Tasha give the triangle?
Solution
First, determine if any of the side lengths are the same.
No
Then, classify the triangle.
Scalene
The answer is a scalene triangle.
Example \(\PageIndex{2}\)
Classify this triangle as scalene, isosceles or equilateral according to its side lengths.
Side lengths, 6 cm, 4 cm, 6 cm
Angles 70, 70, 40 degrees
Solution
First, determine if any of the side lengths are the same.
Yes
Next, determine how many side lengths are the same.
Two
Then, classify the triangle.
Isosceles
The answer is an isosceles triangle.
Example \(\PageIndex{3}\)
Classify this triangle according to its side lengths.
Solution
First, determine if any of the side lengths are the same.
No,
Then, classify the triangle.
Scalene
The answer is a scalene triangle.
Example \(\PageIndex{4}\)
Classify the triangle according to its side lengths.
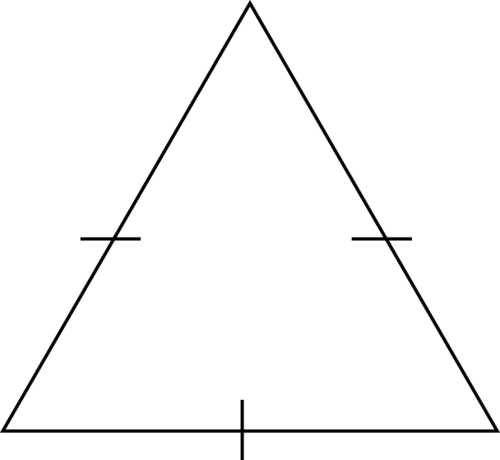Figure \(\PageIndex{5}\)Solution
First, determine if any of the side lengths are the same.
Yes
Next, determine how many side lengths are the same.
All of the side lengths are the same
Then, classify the triangle.
Equilateral
The answer is an equilateral triangle.
Example \(\PageIndex{5}\)
Classify the triangle according to its side lengths.
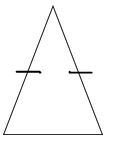
Solution
First, determine if any of the side lengths are the same.
Yes
Next, determine how many side lengths are the same.
Two
Then, classify the triangle.
Isosceles
The answer is an isosceles triangle.
Review
Answer the following questions using what you have learned about triangles their angles and side lengths.
- If a triangle is a right triangle, then how many angles are acute?
- How many angles in a right triangle are right angles?
- How many degrees are there in a right triangle?
- What is an obtuse angle?
- How many obtuse angles are in an obtuse triangle?
- If there is one obtuse angle, how many angles are acute?
- If a triangle is equiangular, what is the measure of all three angles?
- What does the word “interior angle” mean?
- True or false. The side lengths of a scalene triangle are all equal.
- True or false. The side lengths of a scalene triangle are all different.
- True or false. The side lengths of an equilateral triangle are all equal.
- True or false. An isosceles triangle has two side lengths the same and one different.
- True or false. A scalene triangle can also be an isosceles triangle.
- True or false. An equilateral triangle is also equiangular.
- True or false. A scalene triangle can not be an acute triangle.
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.8.
Vocabulary
| Term | Definition |
|---|---|
| Isosceles Triangle | An isosceles triangle is a triangle in which exactly two sides are the same length. |
| Scalene Triangle | A scalene triangle is a triangle in which all three sides are different lengths. |
| Triangle | A triangle is a polygon with three sides and three angles. |
Additional Resources
Interactive Element
Video: Angle Relationships and Types of Triangles
Practice: Classify Triangles by Side Measurement