4.2: Classify Triangles by Angle Measurement
- Page ID
- 2175
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify triangles as acute, right, obtuse or equiangular.
Triangle Classification by Angles

Michael's mother bought a caddy that fits in a corner. She uses the caddy to store their brooms and mops in the garage. His mother's caddy had the appearance of a right triangle when viewed from above and fit perfectly in the corner. Michael liked the caddy, but he couldn't afford to buy one like hers, so he decided to make his own. He bought wood and nails and put it together, but when he tried to put it in the corner in his room, it wouldn't fit. He measures the angles of his caddy and realizes that the top is the triangle below:
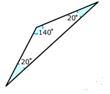
What is the classification of Michael's triangle?
In this concept, you will learn how to use angles to classify triangles.
Classifying Triangles by Angles
The prefix “tri” means three. Triangle means three angles.
To classify a triangle according to its angles, you must look at the angles inside the triangle. Use the number of degrees in these angles to classify the triangle. Let’s look at a picture of a triangle to explain.
Look at the measure of each angle inside the triangle to figure out what kind of triangle it is. There are four types of triangles based on angle measures.
A right triangle is a triangle that has one right angle and two acute angles. One of the angles in the triangle measures \(90^{\circ}\) and the other two angles are less than 90. Here is a picture of a right triangle.
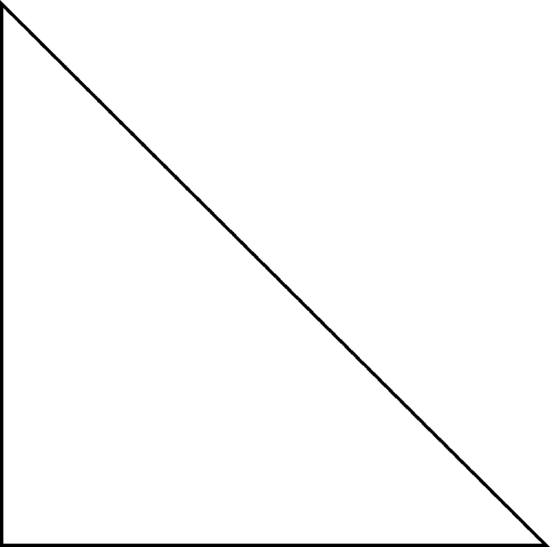
You can see that the 90 degree angle is the one in the bottom left corner. You can even draw in the small box to identify it as a 90 degree angle. If you look at the other two angles you cans see that those angles are less than 90 degrees and are acute.
Let's look at an example of a right angle.

his triangle has one \(90^{\circ}\) angle and two \(45^{\circ}\) angles. Find the sum of the three angles.
\(90+45+45=180^{\circ}\)
The sum of the three angles of a triangle is always equal to \(180^{\circ}\).
In an equiangular triangle, all three of the angles are equal.
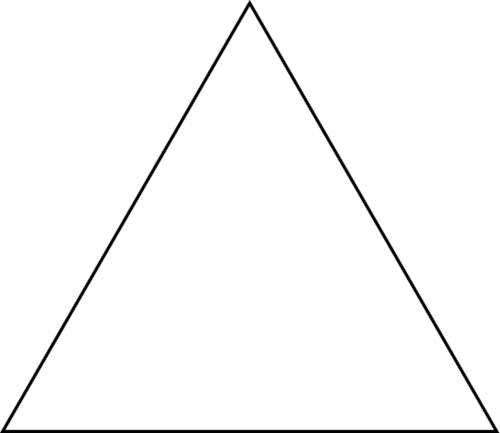
The three angles of this triangle are equal. This is an equiangular triangle.
You know that the sum of the three angles is equal to \(180^{\circ}\), therefore, for all three angles to be equal, each angle must be equal to \(60^{\circ}\).
\(60+60+60=180^{\circ}\)
The sum of the angles is equal to \(180^{\circ}\).
In an acute triangle, all three angles of the triangle are less than 90 degrees. Here is an example of an acute triangle.
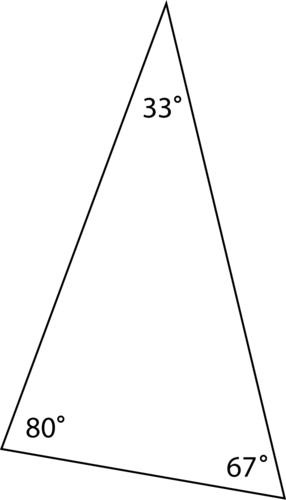
All three of these angles measure less than 90 degrees.
\(33+80+67=180^{\circ}\)
The sum of the angles is equal to \(180^{\circ}\).
An obtuse triangle has one angle that is greater than 90 and two angles that are less than 90.
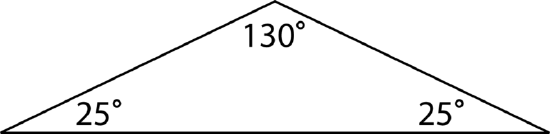
\(130+25+25=180^{\circ}\)
The sum of the angles is equal to \(180^{\circ}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Michael and his caddy.
He tried to build a caddy like his mother's caddy. Her caddy looked like a right triangle from above but he ended up building one that had the following measures and appearance from above:

Solution
What is the classification of Michael's triangle?
First, list the angle measures.
20, 20, 140
Next, determine if any of the angles are equal to 90 degrees or larger than 90 degrees.
Yes, one angle is larger than 90 degrees
Then, classify the triangle.
Obtuse
The answer is an obtuse triangle. Michael created an obtuse triangle instead of a right triangle.
Example \(\PageIndex{2}\)
Identify the type of triangle according to its angles.
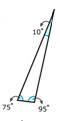
Solution
First, list the angle measures.
10, 75, 95
Next, determine if any of the angles are equal to 90 degrees or larger than 90 degrees.
Yes, one angle is larger than 90 degrees
Then, classify the triangle.
Obtuse
The answer is an obtuse triangle.
Example \(\PageIndex{3}\)
Identify the type of triangle according to its angles.
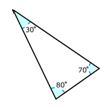
Solution
First, list the angle measures.
30, 70 and 80
Next, determine if any of the angles are equal to 90 degrees or larger than 90 degrees.
No
Then, classify the angle.
Acute
The answer is an acute triangle.
Example \(\PageIndex{}\)
Identify the type of triangle according to its angles.
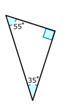
Solution
First, list the angle measures.
35, 55 and 90
Next, determine if any of the angles are equal to 90 degrees or larger than 90 degrees.
Yes, one of the angles is equal to 90 degrees
Then, classify the angle.
Right
The answer is a right triangle
Example \(\PageIndex{5}\)
Classify the triangle by looking at the sum of its angles.
\(40^{\circ}+60^{\circ}+80^{\circ}=180^{\circ}\)
Solution
First, list the angle measures.
40, 60 and 80
Next, determine if any of the angles are equal to 90 degrees or larger than 90 degrees.
No
Then, classify the angle.
Acute
The answer is an acute triangle.
Review
Classify each triangle according to its angles.
-
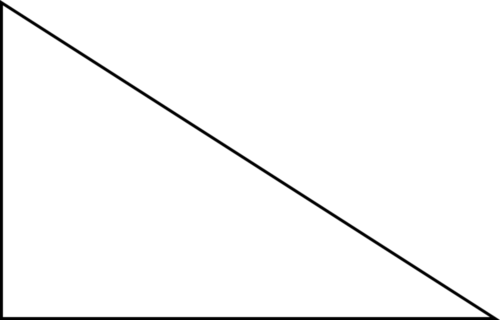
Figure \(\PageIndex{13}\) -
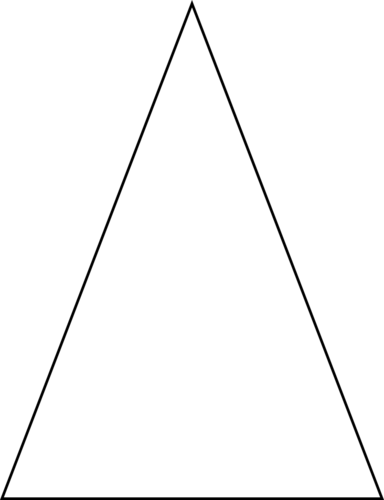
Figure \(\PageIndex{14}\) -
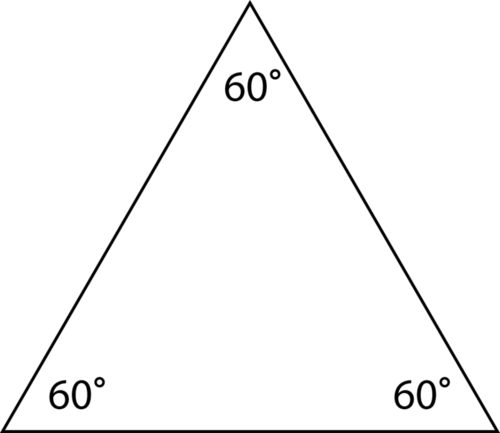
Figure \(\PageIndex{15}\) -
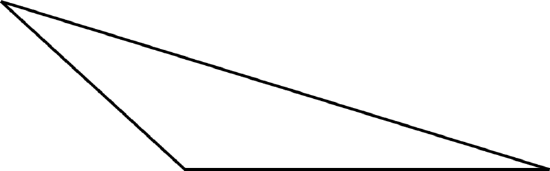
Figure \(\PageIndex{16}\) -
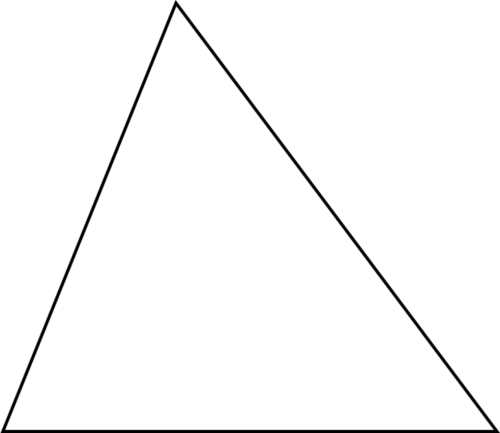
Figure \(\PageIndex{17}\)
Classify the following triangles by looking at the sum of the angle measures.
- \(40+55+45=180^{\circ}\)
- \(20+135+25=180^{\circ}\)
- \(30+90+60=180^{\circ}\)
- \(60+60+60=180^{\circ}\)
- \(110+15+55=180^{\circ}\)
- \(105+65+10=180^{\circ}\)
- \(80+55+45=180^{\circ}\)
- \(70+45+65=180^{\circ}\)
- \(145+20+15=180^{\circ}\)
- \(60+80+40=180^{\circ}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.7.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Acute Triangle | An acute triangle has three angles that each measure less than 90 degrees. |
| Equilateral Triangle | An equilateral triangle is a triangle in which all three sides are the same length. |
| Obtuse Triangle | An obtuse triangle is a triangle with one angle that is greater than 90 degrees. |
| Right Triangle | A right triangle is a triangle with one 90 degree angle. |
| Triangle | A triangle is a polygon with three sides and three angles. |
Additional Resource
Interactive Element
Video: Angle Relationships and Types of Triangles
Practice: Classify Triangles by Angle Measurement

