4.1: Classify Triangles
- Page ID
- 2178
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Classify triangles as acute, right, obtuse or equiangular and as scalene, isosceles or equilateral. Use classifications to find missing information.
Triangle Classification
A triangle is any closed figure made by three line segments intersecting at their endpoints. Every triangle has three vertices (the points where the segments meet), three sides (the segments), and three interior angles (formed at each vertex). All of the following shapes are triangles.
The sum of the interior angles in a triangle is \(180^{\circ}\). This is called the Triangle Sum Theorem and is discussed further in the "Triangle Sum Theorem" concept.
Angles can be classified by their size as acute, obtuse or right. In any triangle, two of the angles will always be acute. The third angle can be acute, obtuse, or right. We classify each triangle by this angle.
Right Triangle: A triangle with one right angle.
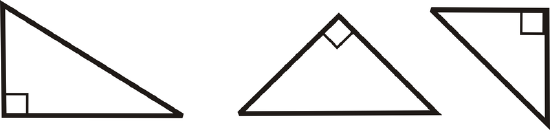
Obtuse Triangle: A triangle with one obtuse angle.
Acute Triangle: A triangle where all three angles are acute.
Equiangular Triangle: A triangle where all the angles are congruent.
You can also classify a triangle by its sides.
Scalene Triangle: A triangle where all three sides are different lengths.
Isosceles Triangle: A triangle with at least two congruent sides.
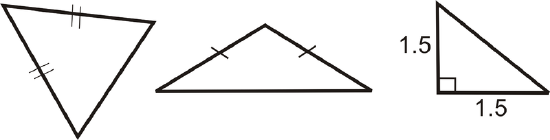
Equilateral Triangle: A triangle with three congruent sides.
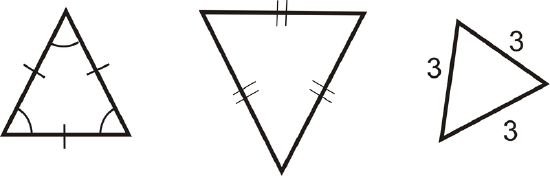
Note that from the definitions, an equilateral triangle is also an isosceles triangle.
What if you were given the angle measures and/or side lengths of a triangle? How would you describe the triangle based on that information?
Example \(\PageIndex{1}\)
Which of the figures below are not triangles?
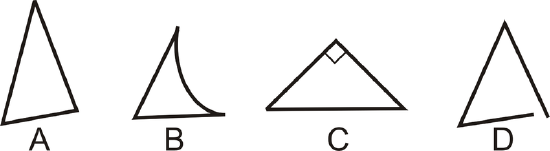Figure \(\PageIndex{9}\)Solution
B is not a triangle because it has one curved side. D is not closed, so it is not a triangle either.
Example \(\PageIndex{2}\)
How many triangles are in the diagram below?
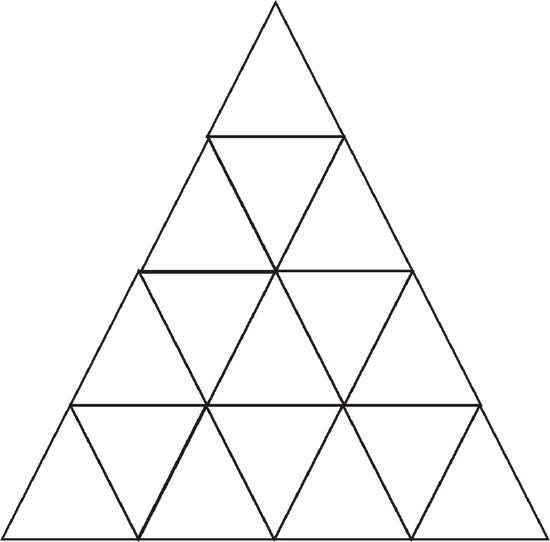Figure \(\PageIndex{10}\)Solution
Start by counting the smallest triangles, 16.
Now count the triangles that are formed by 4 of the smaller triangles, 7.
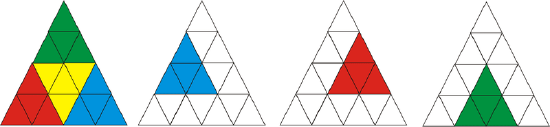Figure \(\PageIndex{11}\)Next, count the triangles that are formed by 9 of the smaller triangles, 3.
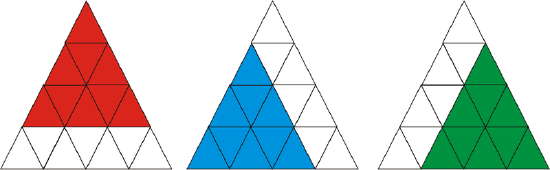
Finally, there is the one triangle formed by all 16 smaller triangles. Adding these numbers together, we get \(16+7+3+1=27\).
Example \(\PageIndex{3}\)
True or false: An equilateral triangle is equiangular.
Solution
True. Equilateral triangles have interior angles that are all congruent so they are equiangular.
Example \(\PageIndex{4}\)
Which term best describes \(\Delta RST\) below?
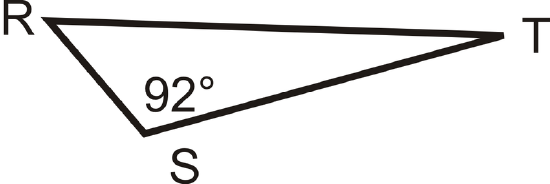
Solution
This triangle has one labeled obtuse angle of \(92^{\circ}\). Triangles can have only one obtuse angle, so it is an obtuse triangle.
Example \(\PageIndex{5}\)
Classify the triangle by its sides and angles.
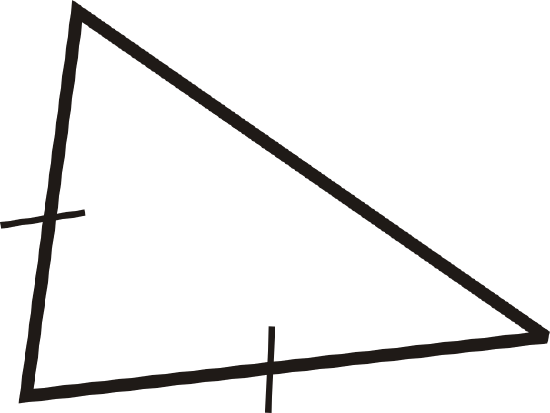
Solution
We see that there are two congruent sides, so it is isosceles. By the angles, they all look acute. We say this is an acute isosceles triangle.
Review
For questions 1-6, classify each triangle by its sides and by its angles.
-
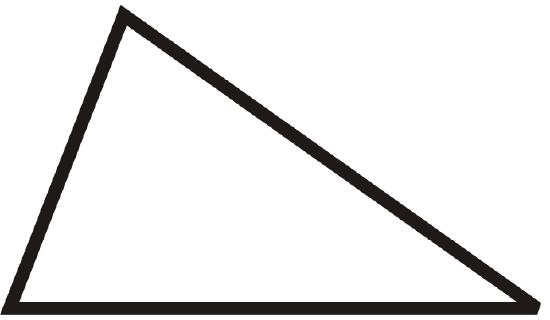
Figure \(\PageIndex{15}\) -
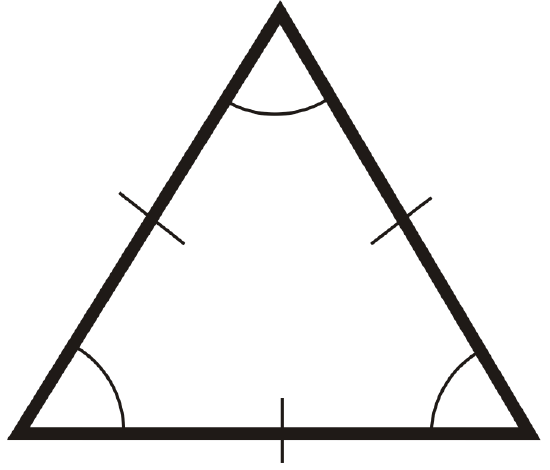
Figure \(\PageIndex{16}\) -
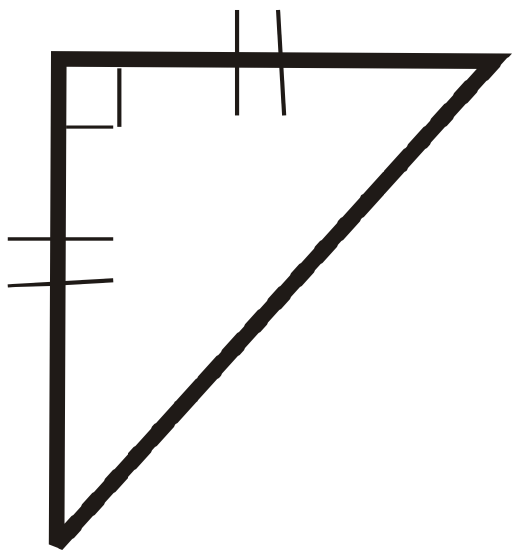
Figure \(\PageIndex{17}\) -
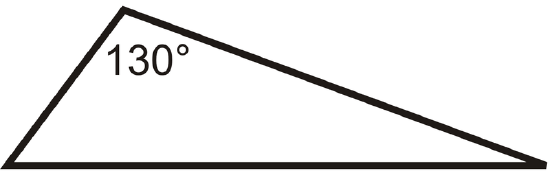
Figure \(\PageIndex{18}\) -
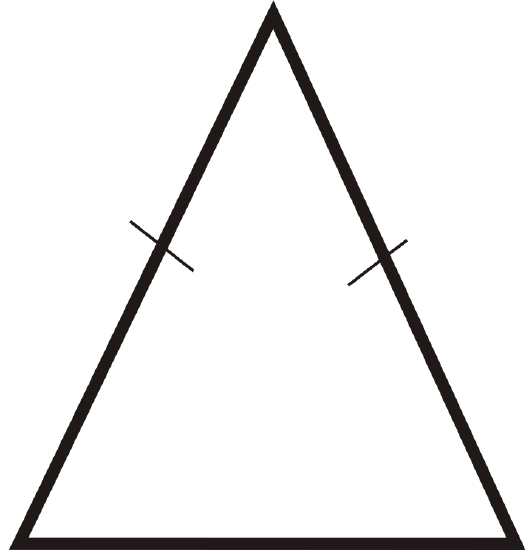
Figure \(\PageIndex{19}\) -
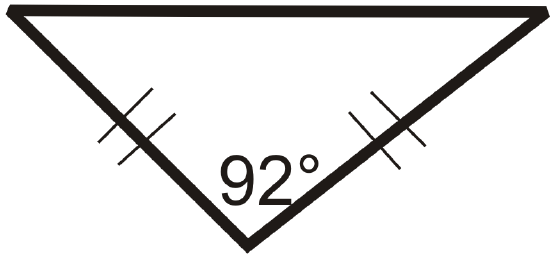
Figure \(\PageIndex{20}\) - Can you draw a triangle with a right angle and an obtuse angle? Why or why not?
- In an isosceles triangle, can the angles opposite the congruent sides be obtuse?
For 9-10, determine if the statement is true or false.
- Obtuse triangles can be isosceles.
- A right triangle is acute.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.11.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Acute Triangle | An acute triangle has three angles that each measure less than 90 degrees. |
| equiangular triangle | A triangle with all congruent angles. |
| equilateral triangle | A triangle with three congruent sides. |
| Isosceles Triangle | An isosceles triangle is a triangle in which exactly two sides are the same length. |
| Obtuse Triangle | An obtuse triangle is a triangle with one angle that is greater than 90 degrees. |
| Scalene Triangle | A scalene triangle is a triangle in which all three sides are different lengths. |
| Triangle | A triangle is a polygon with three sides and three angles. |
| Interior angles | Interior angles are the angles inside a figure. |
| Right Angle | A right angle is an angle equal to 90 degrees. |
| Equilateral | A polygon is equilateral if all of its sides are the same length. |
| Equiangular | A polygon is equiangular if all angles are the same measure. |
Additional Resources
Interactive Element
Video: Angle Relationships and Types of Triangles
Activities: Triangle Classification Discussion Questions
Study Aids: Polygons Study Guide
Practice: Classify Triangles
Real World: Bridges Over Troubled Water