4.5: Equilateral Triangles

Properties of triangles with three equal sides.

Equilateral Triangle Theorem: All equilateral triangles are also equiangular. Furthermore, all equiangular triangles are also equilateral.

Figure $\PageIndex{1}$

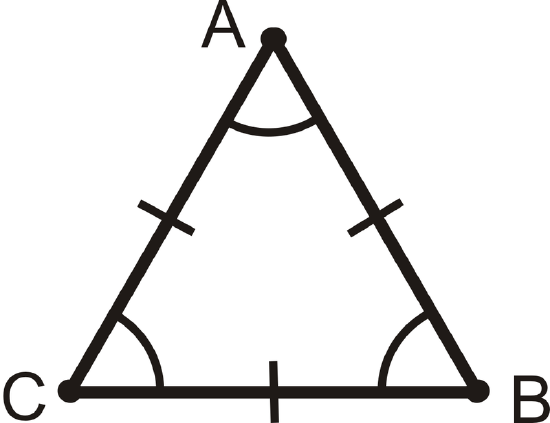
If $\overline{AB}\cong \overline{BC}\cong \overline{AC}$, then $\angle A\cong \angle B\cong \angle C$. Conversely, if $\angle A\cong \angle B\cong \angle C$, then $\overline{AB}\cong \overline{BC}\cong \overline{AC}$.

What if you were presented with an equilateral triangle and told that its sides measure $x$, $y$, and 8? What could you conclude about $x$ and $y$?

Example $\PageIndex{1}$

Fill in the proof:

Given: Equilateral $\Delta RST$ with

$\overline{RT}\cong \overline{ST}\cong \overline{RS}$

Prove: $\Delta RST$ is equiangular

Figure $\PageIndex{2}$

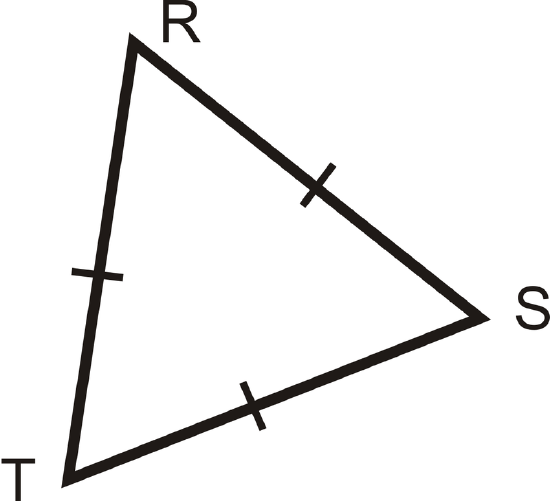
Solution

Statement	Reason
1.	1. Given
2.	2. Base Angles Theorem
3.	3. Base Angles Theorem
4.	4. Transitive $PoC$
5. $\Delta RST$ is equiangular	5.

Statement	Reason
1. $RT\overline{AB}\cong ST\overline{AB}\cong RS\overline{AB}$	1. Given
2. $\angle R\cong \angle S$	2. Base Angles Theorem
3.$\angle T\cong \angle R$	3. Base Angles Theorem
4. $\angle T\cong \angle S$	4. Transitive $PoC$
5. $\Delta RST$ is equiangular	5. Definition of equiangular.

Example $\PageIndex{2}$

True or false: All equilateral triangles are isosceles triangles.

Solution

This statement is true. The definition of an isosceles triangle is a triangle with at least two congruent sides. Since all equilateral triangles have three congruent sides, they fit the definition of an isosceles triangle.

Example $\PageIndex{3}$

Find the value of $x$.

Figure $\PageIndex{3}$

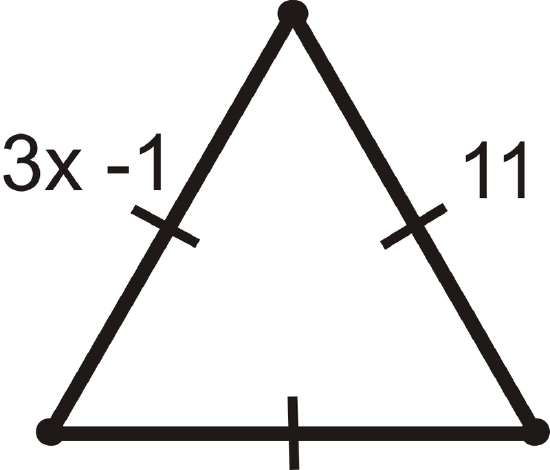
Solution

Because this is an equilateral triangle $3x−1=11$. Solve for $x$.

$\bgin{align*} 3x−1&=11 \\3x&=12 \\ x&=4 \end{align*}$

Example $\PageIndex{4}$

Find the values of $x$ and $y$.

Figure $\PageIndex{3}$

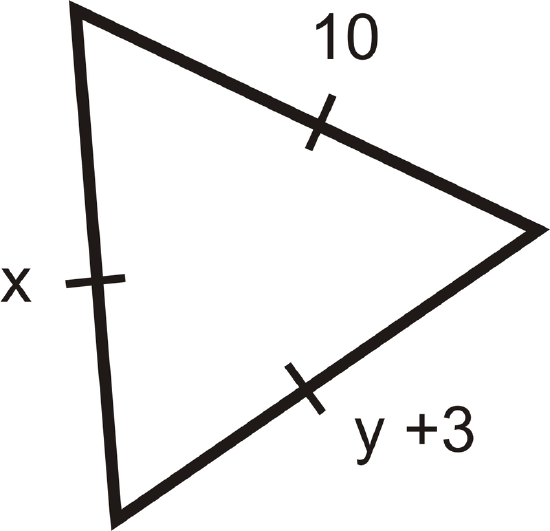
Solution

The markings show that this is an equilateral triangle since all sides are congruent. This means all sides must equal $10$. We have $x=10$ and $y+3=10$ which means that $y=7$.

Example $\PageIndex{5}$

Two sides of an equilateral triangle are $2x+5$ units and $x+13$ units. How long is each side of this triangle?

Solution

The two given sides must be equal because this is an equilateral triangle. Write and solve the equation for $x$.

$\egin{align*}2x+5 &=x+13 \\ x&=8 \end{align*}$

To figure out how long each side is, plug in 8 for $x$ in either of the original expressions. $2(8)+5=21$. Each side is $21$ units.

Review

The following triangles are equilateral triangles. Solve for the unknown variables.

1. 

   Figure $\PageIndex{4}$

2. 

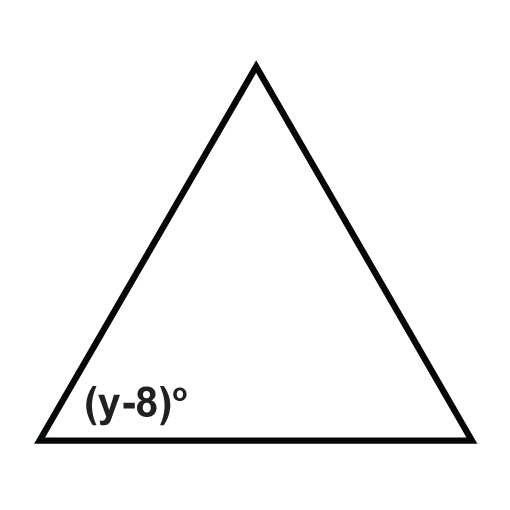
   Figure $\PageIndex{5}$

3. 

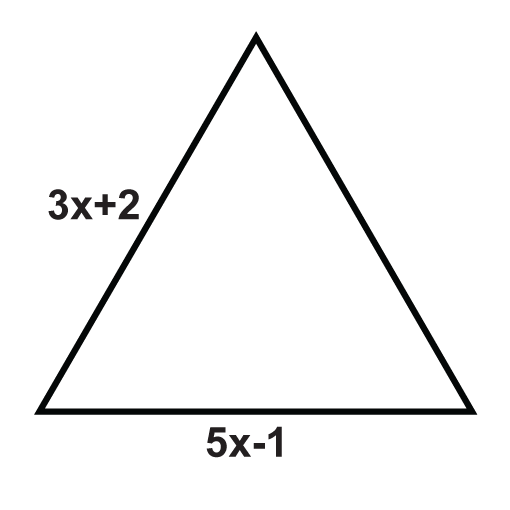
   Figure $\PageIndex{6}$

4. 

   Figure $\PageIndex{7}$

5. 

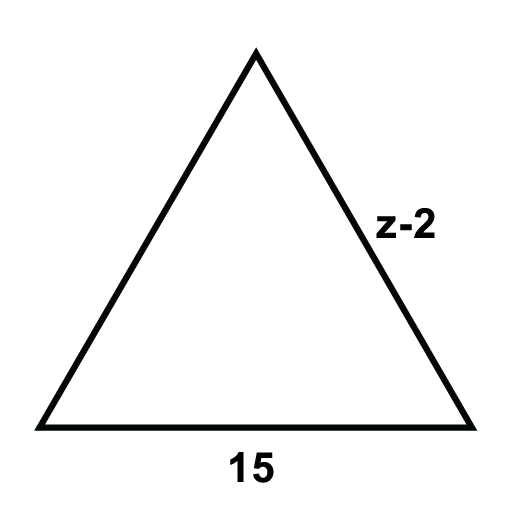
   Figure $\PageIndex{8}$

6. 

   Figure $\PageIndex{9}$

7. 

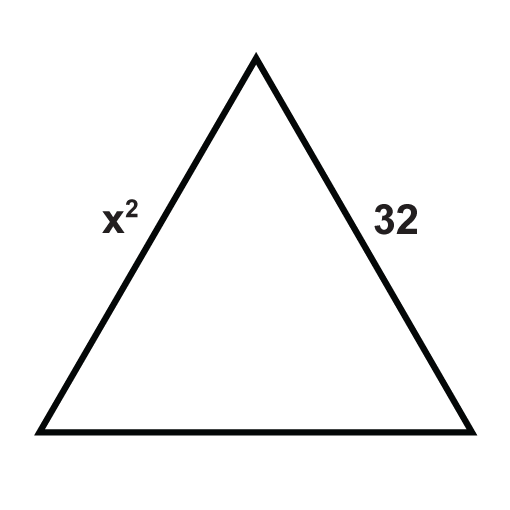
   Figure $\PageIndex{10}$

8. 

   Figure $\PageIndex{11}$

9. 

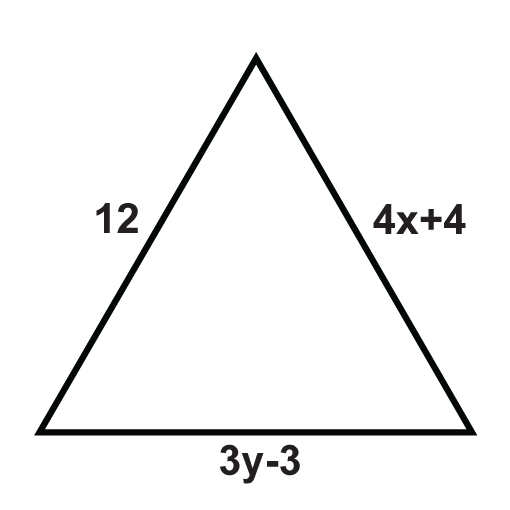
   Figure $\PageIndex{12}$

10. 

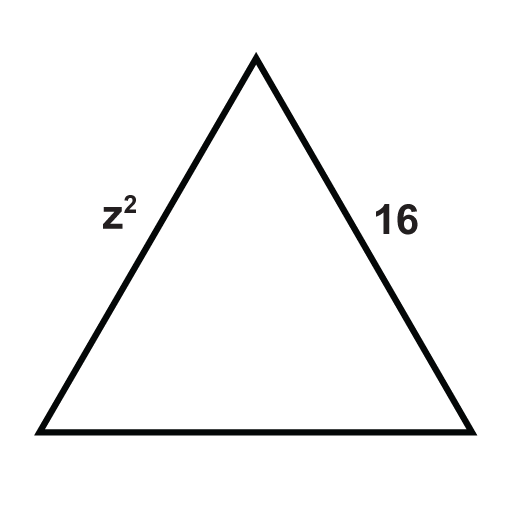
    Figure $\PageIndex{13}$

11. 

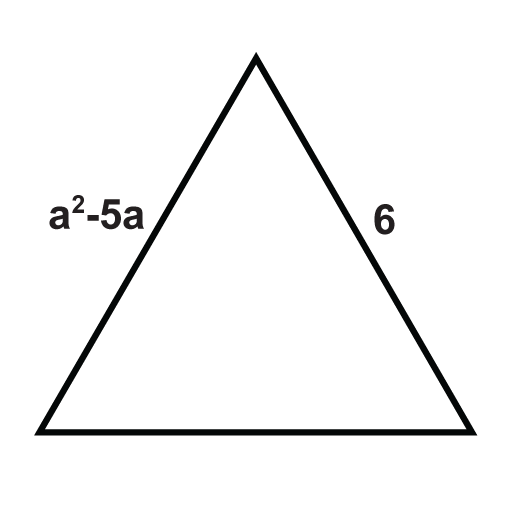
    Figure $\PageIndex{14}$

12. 

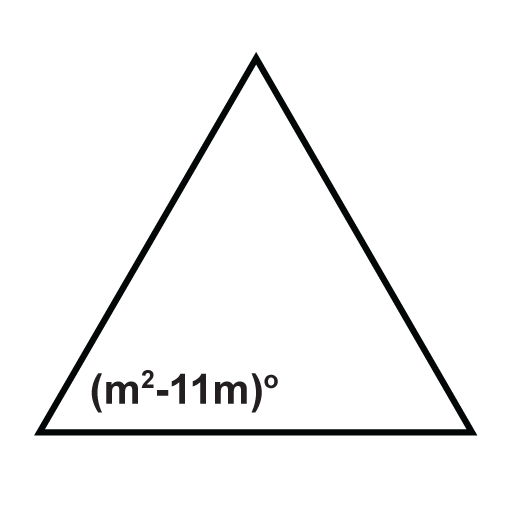
    Figure $\PageIndex{15}$

13. 

    Figure $\PageIndex{16}$

14. 

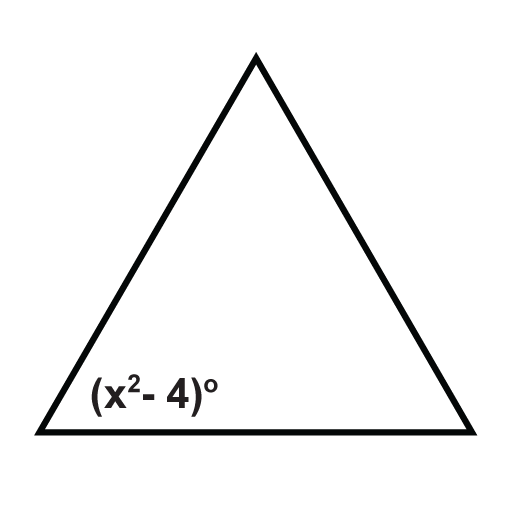
    Figure $\PageIndex{17}$

15. Find the measures of $x$ and $y$.

Figure $\PageIndex{18}$

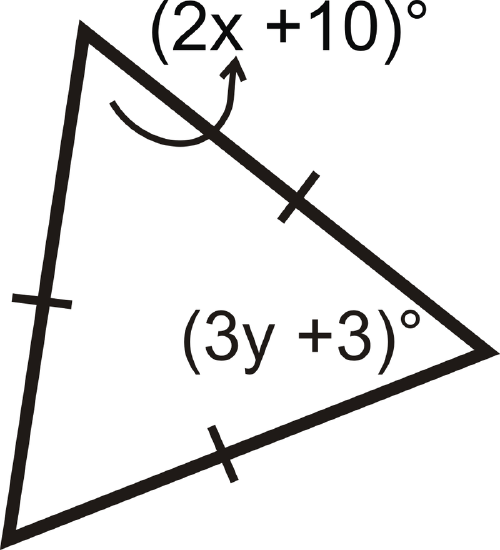
Review (Answers)

To see the Review answers, open this PDF file and look for section 4.11.

Additional Resources

Interactive Element

Video: Equilateral Triangles Principles - Basic

Activities: Equilateral Triangles Discussion Questions

Study Aids: Equilateral Triangles Discussion Questions

Practice: Equilateral Triangles

Real World: Equilateral Triangles