4.7: Triangle Area
- Page ID
- 4802
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Terry has two tickets to his favorite college football team’s next home game, so he is planning to take his younger brother with him to the game. Terry wants to make two pennants for the game, so he buys a piece of material shaped like a rectangle with a base of 18 inches and a height of 12 inches. Terry plans to divide the material into two triangles. How can Terry figure out the area of each of the triangles that will be cut from the material for his pennants?
In this concept, you will learn to find the areas of triangles given a base and a height.
Finding the Area of a Triangle
Triangles are not parallelograms because they only have three sides, but they are related to parallelograms. Take a look the parallelogram below and see if you can figure out the connection.

If you look carefully, you will notice that the parallelogram can be divided into two triangles.
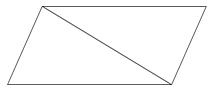
A rectangle is a type of parallelogram with four right angles. You can divide a rectangle into two triangles also.
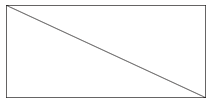
Notice that a rectangle is divided into two right triangles, triangles containing a right angle.
A square is a type of rectangle with four equal sides and four right angles. A square can also be divided into two right triangles.
If a parallelogram can be divided into two triangles, then the area of a triangle is one-half the area of a parallelogram.
Let’s look at how this works.
What is the area of this parallelogram?

To find the area of the parallelogram, multiply the base by the height.
\(\begin{align*} A &=bh\\ A&=2(5)\\ A&=10 sq.\: inches.\end{align*} \)
A parallelogram can be divided into two triangles.
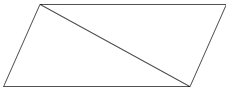
If you divide the area of the parallelogram in half, that will give you the area of one of the triangles.
\(10\div 2=5 sq.\: inches\)
Based on this information, you can write the following formula for finding the area of a triangle.
\(A=\dfrac{1}{2}bh\)
A triangle is one-half of a parallelogram, so the formula for the parallelogram multiplied by one-half is the formula for finding the area of a triangle.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Terry and his sports pennants.
Terry has always been a Gator football fan, so he is excited about attending one of the team’s home games. He has purchased material to make two pennants for the game. The material is shaped like a rectangle, and Terry plans to divide it into two triangles for the pennants. The material has a 38-inch base and a height of 30 inches. Terry wants to know the size of the two triangles after he cuts the material. How can Terry figure out the area of each of the triangles that will form his pennants?
Solution
Here is a look at the piece of material.
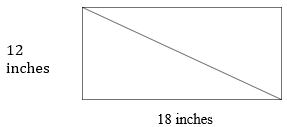
First, recall that the area of a rectangle is base times height and a triangle is one half the area of a rectangle.
\(\begin{align*}Base\times Height &=Area \:of \:a\: Rectangle \\ 18\times 12&=216 \\ &=216 \: square \:inches \end{align*}\)
Next, substitute the area value for the rectangle (or the base\times height) in the triangle area formula.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(216) \end{align*}\)
Then, solve the equation.
\(\begin{align*}A&=\dfrac{1}{2}(216) \\ A&=108\: square\: inches \end{align*}\)
The answer is each of the triangles will have an area of 108 square inches.
Example \(\PageIndex{2}\)
Find the area of the triangle with a base of 6 feet and a height of 5 feet.
Solution
First, substitute the values for the base and height into the triangle area formula.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=12(6)(5) \end{align*}\)
Next, solve the equation.
\(\begin{align*}A&=12(30) \\ A&=15\: square feet \end{align*}\)
The answer is 15 square feet.
Example \(\PageIndex{3}\)
Using the area of the following parallelogram, find the area of one of the triangles inside the parallelogram.
Solution
Area of a rectangle is 12 sq. inches
First, recall that the area of a rectangle is base times height and a triangle is one half the area of a rectangle.
Next, substitute the area value for the base and height in the triangle area formula.
\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(12) \end{align*}\)
Then, solve the equation.
\(\begin{align*}A&=\dfrac{1}{2}(12) \\ A&=6\: square \:inches \end{align*}\)
The answer is 6 square inches.
Example \(\PageIndex{4}\)
Using the area of the following parallelogram, find the area of one of the triangles inside the parallelogram.
Solution
Area of a parallelogram is 24 sq. feet
First, recall that the area of a parallelogram is base times height and a triangle is one half the area of a parallelogram.
Next, substitute the area value for the base and height in the triangle area formula.
\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(24) \end{align*}\)
Then, solve the equation.
\(\begin{align*} A&=\dfrac{1}{2}(24) \\ A&=12\: square\: feet \end{align*}\)
The answer is 12 square feet.
Example \(\PageIndex{5}\)
Using the area of the following parallelogram, find the area of one of the triangles inside the parallelogram.
Solution
Area of a parallelogram is 18 sq. feet
First, substitute the area value for the base and height in the triangle area formula.
\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(18)\end{align*}\)
Then, solve the equation.
\(\begin{align*} A&=\dfrac{1}{2}(18) \\ A&=9\: square\: feet \end{align*}\)
The answer is 9 square feet.
Review
Find the area of each triangle given the following measurements.
-
Figure \(\PageIndex{6}\)
Base = 10 in, Height = 4 in
-

Figure \(\PageIndex{7}\) Base = 16 meters, Height = 10 meters
-
Figure \(\PageIndex{8}\)
Base = 8 in, Height = 6.5 in
-
Figure \(\PageIndex{9}\)
Base = 10 cm, Height = 7 cm
-

Figure \(\PageIndex{10}\)
Base = 5 ft, Height = 8.5 feet
Find the area of each triangle given the base and height.
- Base = 4 in, Height = 5 in
- Base = 6 in, Height = 4 in
- Base = 8 ft, Height = 7 ft
- Base = 10 meters, Height = 8 meters
- Base = 10 meters, Height = 5 meters
- Base = 12 feet, Height = 14 feet
- Base = 11 feet, Height = 6 feet
- Base = 14 inches, Height = 8 inches
- Base = 22 feet, Height = 19 feet
- Base = 30 cm, Height = 28 cm
- Base = 18 inches, Height = 16 inches
- Base = 13 meters, Height = 10 meters
- Base = 18 meters, Height = 5.5 meters
- Base = 12.5 feet, Height = 2.5 feet
- Base = 13.75 inches, Height = 1.5 inches
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.3.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Rectangle | A rectangle is a quadrilateral with four right angles. |
| Square | A square is a polygon with four congruent sides and four right angles. |
Additional Resources
Interactive Element
Video: Area of a Triangle (Whole Numbers)
Practice: Triangle Area
Real World: Building Triangles

