4.28: Basics of Pythagorean Theorem
- Page ID
- 4960
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify triples and calculate missing sides. Use indirect measurement applications
Derive and Use the Pythagorean Theorem

Tracy’s kitten is stuck 2.8 yards above the ground on the window sill of her Grandma’s house. Her grandma is not at home so she decides to rescue her terrified kitten with help from her friends. For safety reasons, the base of the ladder must be 0.7 yards away from the house and extend 1 yard above the window sill. The ladder she has borrowed is 4 yards in length.
As Tracy positions the ladder in place, she looks up and wonders if the ladder is going to be tall enough for her to rescue her kitten.
In this concept, you will learn to derive and use the Pythagorean Theorem.
Pythagorean Theorem
Triangles are often named according to the measure of the angles they contain. An acute triangle has three angles such that each of the three angles is less than \(90^{\circ}\). An obtuse triangle has two angles such that the measure of each of these angles is less than \(90^{\circ}\) and the measure of the third angle is greater than \(90^{\circ}\). A right triangle has one angle that has a measure of \(90^{\circ}\) and two acute angles such that the sum of their measures equals \(90^{\circ}\). The two acute angles of a right triangle are complementary – their sum equals \(90^{\circ}\).
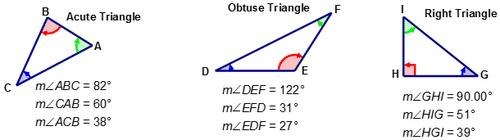
Of the three triangles shown in the above diagram, the right triangle is the one that is used most often in solving real world problems. This type of triangle has characteristics that are unique only to right triangles. Every triangle has three sides and three angles. The sides of a right triangle have names that apply only to a right triangle.
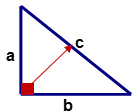
The two sides of the right triangle labeled ‘a’ and ‘b’ are called the legs of the triangle. The side of the triangle opposite the right angle (\(90^{\circ}\)) labeled ‘c’ is called the hypotenuse and it is the longest side of the right triangle. The names of the legs ‘a’ and ‘b’ can be switched from one leg to the other but the hypotenuse ‘c’ must be the side opposite the right angle of the triangle.
The relationship between the hypotenuse and the legs of a right triangle is defined by the Pythagorean Theorem which states that the square of the length of the hypotenuse is equal to the sum of the length of leg ‘a’ squared and the length of leg ‘b’ squared. The Pythagorean Theorem is stated by the equation.
\(c^2= a^2+b^2\)
The equation representing the Pythagorean Theorem contains three pieces which are a,b and c. If you know two of these pieces, then the equation can be used to calculate the third piece. The Pythagorean Theorem can also be used to determine if a given triangle is indeed a right triangle.
Look at the triangle given below. There is no right angle marked to indicate that the triangle is a right triangle. Is the triangle a right triangle? The Pythagorean Theorem can be used to answer this question.
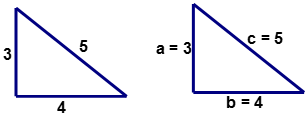
\(c^2=a^2+b^2\)
First, fill in the values for the letters \(a\),\(b\) and \(c\).
\(\begin{align*}c^2&=a^2+b^2 \\ (5)^2&=(3)^2+(4)^2\end{align*}\)
Next, perform the indicated operations on both sides of the equation.
\(\begin{align*}(5)^2&=(3)^2+(4)^2 \\ (5\times 5)&=(3\times 3)+(4\times 4) \\ 25&=9+16\end{align*}\)
Then, simplify the equation by adding the values on the right side of the equation.
\(\begin{align*}25&=9+16 \\ 25&=25\end{align*}\)
Both sides of the equation are equal. The values of (3, 4, and 5) resulted in \(c^2=a^2+b^2 being a true statement of equality. Therefore, the given triangle is a right triangle.
The values of (3, 4, and 5) for the positive integers (a,b,c) respectively, is a combination of numbers known as a Pythagorean Triple which are a set of three whole numbers that satisfy the Pythagorean Theorem \(c^2=a^2+b^2\). Other Pythagorean Triples can be generated by multiplying the values of any known Pythagorean Triple by any positive integer. If the values (3, 4, and 5) are multiplied by 2 then another Pythagorean Triple (6, 8, and 10) is created. If the values (6, 8, and 10) are multiplied by 4 then another Pythagorean Triple (24, 32, and 40) is generated.
The newly generated values have been substituted into the Pythagorean Theorem, \(c^2=a^2+b^2\), to ensure that they are Pythagorean Triples.
\(\begin{align*} c^2&=a^2+b^2 &\qquad c^2&=a^2+b^2 \\ (10)^2&=(6)^2+(8)^2 &\qquad (40)^2&=(24)^2+(32)^2 \\ (10\times 10)&=(6\times 6)+(8\times 8)&\qquad (40\times 40)&=(24\times 24)+(32\times 32) \\ 100&=36+64&\qquad 1600&=576+1024 \\ 100&=100 &\qquad 1600&=1600\end{align*}\)
Each of the new Pythagorean Triples have resulted in \(c^2=a^2+b^2\) being a true statement of equality.
If you know that a given triangle is a right triangle, then the Pythagorean Theorem can be used to calculate the length of an unknown side of the triangle when you know the lengths of two of the sides.
Let’s look at an example.
For the following right triangle, calculate the length of the unknown side ‘\(b\)?’
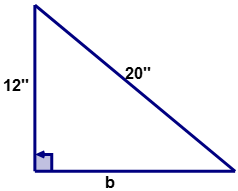
First, use the Pythagorean Theorem to calculate the length of side ‘\(b\).’
\(c^2= a^2+b^2\)
Next, fill in the values given for sides ‘\(a\)’ and side ‘\(c\).’
\(\begin{align*}c^2&=a^2+b^2 \\ (20)^2&=(12)^2+b^2\end{align*}\)
Next, perform the indicated operations.
\(\begin{align*}(20)^2&=(12)^2+b^2 \\ (20\times 20)&=(12\times 12)+b^2 \\ 400&=144+b^2\end{align*}\)
Next, subtract 144 from both sides of the equation to isolate the variable and simplify both sides of the equation.
\(\begin{align*}400&=144+b^2 \\ 400−144&=144−144+b^2 \\ 256&=b^2\end{align*}\)
Then, solve for ‘b’ by taking the square root of both sides of the equation. Remember taking the square root is the inverse operation of squaring.
\(\begin{align*}256&=b^2 \\ \sqrt{256}&=\sqrt{b^2} \\ 16&=b\end{align*}\)
The answer is 16.
The length of side ‘\(b\)’ is 16 inches.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Tracy and her rescue mission. She needs to know if the ladder she is using is long enough to rescue her kitten.
Solution
First, draw and label a picture to model the problem.
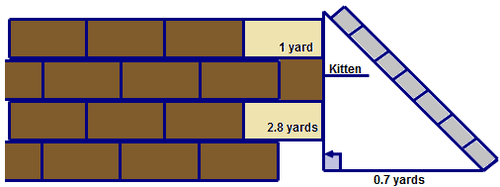
Next, look at the right triangle and determine the measurements of the two known sides.
\(a=3.8\:yards\)
\(b=0.7\:yards\)
Next, use the Pythagorean Theorem to calculate the length of the ladder which is the hypotenuse of the right triangle.
\(c^2= a^2+b^2\)
First, fill in the values for ‘a’ and ‘b.’
\(\begin{align*}c^2&=a^2+b^2 \\ c^2&=(3.8)^2+(0.7)^2\end{align*}\)
Next, perform the indicated operations and simplify the equation.
\(\begin{align*}c^2&=(3.8\times 3.8)+(0.7\times 0.7) \\ c^2&=14.44+0.49 \\ c^2&=14.93\:yards\end{align*}\)
Then, solve for ‘c’ by taking the square root of each side of the equation.
\(\begin{align*}c^2&=14.93 \\ \sqrt{c^2}&=\sqrt{14.93} \\ c&=3.86\end{align*}\)
The answer is 3.86.
The ladder must be 3.86 yards in length to rescue the kitten. The ladder Tracy is using is long enough.
Example \(\PageIndex{2}\)
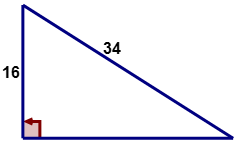
Use the Pythagorean Theorem to calculate the length of the missing side of the following right triangle:
Solution
First, determine what the given values represent and what side is missing?
\(\begin{align*} a&=16 \\ b&=? \\ c&=34\end{align*}\)
Next, substitute the given values into equation that represents the Pythagorean Theorem.
\(\begin{align*}c^2&=a^2+b^2 \\ (34)^2&=(16)^2+b^2\end{align*}\)
Next, perform the indicated operations on both sides of the equation.
\(\begin{align*}(34)^2&=(16)^2+b^2 \\ (34\times 34)&=(16\times 16)+b^2 \\ 1156&=256+b^2\end{align*}\)
Next, subtract 256 from both sides of the equation to isolate the variable.
\(\begin{align*}1156&=256+b^2 \\ 1156−256&=256−256+b^2\end{align*}\)
Next, simplify the equation.
\(\begin{align*}1156−256&=256−256+b^2 \\ 900&=b^2\end{align*} \)
Then, take the square root of both sides of the equation to solve for the variable ‘\(b\).’
\(\begin{align*} 900&=b^2 \\ \sqrt{900}&=\sqrt{b^2} \\ 30&=b\end{align*}\)
The answer is \(b=30\).
Example \(\PageIndex{3}\)
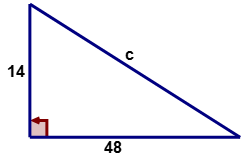
Find the length of the hypotenuse of a right triangle given the lengths of legs ‘\(a\)’ and ‘‘\(b\)’ are 14 and 48 centimeters, respectively.
Solution
First, draw and label a right triangle to represent the given information.
Next, substitute the given values into equation that represents the Pythagorean Theorem.
\(\begin{align*} c^2&= a^2+b^2 \\ c^2&= (14)^2+(48)^2\end{align*}\)
Next, perform the indicated operations and simplify the equation.
\(\begin{align*} c^2= (14)^2+(48)^2 \\ c^2&= (14\times 14)+(48\times 48) \\ c^2&= 196+2304\end{align*} \)
Next, simplify the equation by adding the values on the right side of the equation.
\(\begin{align*} c^2&= 196+2304 \\ c^2&= 2500\end{align*}\)
Then, take the square root of both sides of the equation to solve for the variable ‘\(c\).’
\(\begin{align*} c^2&= 2500 \\ \sqrt{c^2}&=2500 \\ c&=50\end{align*}\)
The answer is \(c=50\).
The length of the hypotenuse is 50 cm.
Example \(\PageIndex{4}\)
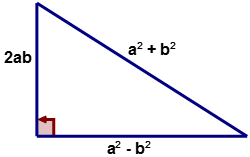
If ‘\(a\)’ and ‘\(b\)’ are values such that \(a,\:b\in N\) and \(a>b\) then the sides of a right triangle are \(a^2+b^2\), \(a^2−b^2\), and \(2ab\) as shown in the diagram below.
Solution
Complete the following table to generate Pythagorean Triples.
| \(av | \( b\) | \(a^2−b^2\) | \(2ab\) | \(a^2+b^2\) |
| 4 | 2 | 12 | 16 | 20 |
| 5 | 3 | 16 | 30 | 34 |
| 6 | 4 | 20 | 48 | 52 |
First, using \(a=4 and \(b=2\) evaluate \(a^2−b^2\) by substituting the given values into the expression.
\(\begin{align*} &a^2−b^2 \\ &(4)^2−(2)^2\end{align*}\)
Next, perform the indicated operations and simply the expression.
\(\begin{align*} &(4)^2−(2)^2 \\ &(4\times 4)−(2\times 2) \\ &16−4 \\ &12\end{align*} \)
The answer is 12.
Then, place the answer in the table in the correct column.
Now, complete the \(a^2−b^2\) column for the remaining given values of ‘\(a\)’ and ‘\(b\).’
First, using \(a=5\) and \(b=3\) evaluate \(a^2−b^2\) by substituting the given values into the expression.
\(\begin{align*} &a^2−b^2 \\ &(5)^2−(3)^2\end{align*} \)
Next, perform the indicated operations and simply the expression.
\(\begin{align*} (5)^2−(3)^2 \\ (5\times 5)−(3\times 3) \\ 25−9=16\end{align*} \)
The answer is 16.
Then, place the answer in the table in the correct column.
First, using \(a=6\) and \(b=4\) evaluate \(a^2−b^2\) by substituting the given values into the expression.
\(\begin{align*} &a^2−b^2 \\ &(6)^2−(4)^2 \end{align*}\)
Next, perform the indicated operations and simply the expression.
\(\begin{align*} (6)^2−(4)^2 \\ &(6\times 6)−(4\times 4) \\ &36−16 \\ &20 \end{align*} \)
The answer is 20.
Then, place the answer in the table in the correct column.
First, using \(a=4\) and \(b=2\) evaluate \(2ab\) by substituting the given values into the expression.
\(2ab\)
\(2(4)(2)\)
Next, perform the indicated operations.
\(2(4)(2)\)
\(8(2)\)
\(16\)
The answer is 16.
Then, place the answer in the table in the correct column.
Now, complete the \(2ab\) column for the remaining given values of ‘\(a\)’ and ‘\(b\).’
First, using \(a=5\) and \(b=3\) evaluate \(2ab\) by substituting the given values into the expression.
\(\begin{align*} &2ab \\ &2(5)(3)\end{align*}\)
Next, perform the indicated operations.
\(\begin{align*} &2(5)(3) \\ &10(3) \\ &30\end{align*}\)
The answer is 30.
Then, place the answer in the table in the correct column.
First, using \(a=6\) and \(b=4\) evaluate \(2ab\) by substituting the given values into the expression.
\(\begin{align*} &2ab \\ &2(6)(4)\end{align*}\)
Next, perform the indicated operations.
\(\begin{align*}&2(6)(4) \\ &12(4) \\ &48\end{align*}\)
The answer is 48.
Then, place the answer in the table in the correct column.
First, using \(a=4\) and \(b=2\) evaluate \(a^2+b^2\) by substituting the given values into the expression.
\(\begin{align*} &a^2+b^2 \\ &(4)^2(2)^2\end{align*} \)
Next, perform the indicated operations and simply the expression.
\(\begin{align*} &(4)^2+(2)^2 \\ &(4\times 4)+(2\times 2)16+4 \\ &20\end{align*}\)
The answer is 20.
Then, place the answer in the table in the correct column.
Now, complete the \(a^2+b^2\) column for the remaining given values of ‘\(a\)’ and ‘\(b\).’
First, using \(a=5\) and \(b=3\) evaluate \(a^2+b^2\) by substituting the given values into the expression.
\(\begin{align*} &a^2+b^2 \\ &(5)^2+(3)^2\end{align*}\)
Next, perform the indicated operations and simply the expression.
\( \begin{align*} &(5)^2+(3)^2 \\ &(5\times 5)+(3\times 3) \\ &25+9 \\ &34 \end{align*}\)
The answer is 34.
Then, place the answer in the table in the correct column.
First, using \(a=6\) and \(b=4\) evaluate \(a^2+b^2\) by substituting the given values into the expression.
\(a^2+b^2\)
\((6)^2+(4)^2\)
Next, perform the indicated operations and simply the expression.
\(\begin{align*} &(6)^2+(4)^2 \\ &(6\times 6)+(4\times 4) \\ &36+16 \\ &52\end{align*}\)
The answer is 52.
Then, place the answer in the table in the correct column.
Example \(\PageIndex{5}\)
Use the Pythagorean Theorem to find the length of the missing leg of the following right triangle.
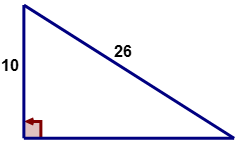
Solution
First, determine what the given values represent and what side is missing?
\(\begin{align*} a&=? \\ b&=10 \\ c&=26\end{align*} \)
Next, substitute the given values into equation that represents the Pythagorean Theorem.
\(\begin{align*} c^2&=a^2+b^2 \\ (26)^2&=a^2+(10)^2\end{align*}\)
Next, perform the indicated operations and simplify the equation.
\(\begin{align*} (26)^2&=a^2+(10)^2 \\ (26\times 26)&=a^2+(10\times 10) \\ 676&=a^2+100\end{align*}\)
Next, subtract 100 from both sides of the equation to isolate the variable.
\(\begin{align*} 676&=a^2+100 \\ 676−100&=a^2+100−100 \end{align*} \)
Next, simplify the equation.
\(\begin{align*} 676−100&=a^2+100−100 \\ 576&=a^2\end{align*}\)
Then, take the square root of both sides of the equation to solve for the variable ‘a.’
\(\begin{align*}576&=a^2 \\ \sqrt{576}&=\sqrt{a^2} \\ 24&a\end{align*}\)
The answer is \(a=24\).
Review
Use the Pythagorean Theorem to find the missing dimensions of each right triangle.
- \(a=3,\:b=4,\:c=?\)
- \(a=6,\:b=8,\:c=?\)
- \(a=9,\:b=12,\:c=?\)
- \(a=27,\:b=36,\:c=?\)
- \(a=15,\:b=20,\:c=?\)
- \(a=18,\:b=24,\:c=?\)
- \(a=?,\:b=16,\:c=20\)
- \(a=?,\:b=28,\:c=35\)
- \(a=30,\:b=?,\:c=50\)
- \(a=33,\:b=?,\:c=55\)
- \(a=1.5,\:b=?,\:c=2.5\)
- \(a=36,\:b=?,\:c=60\)
State whether the following statements are True or False.
- The Pythagorean Theorem will work for any triangle.
- The longest side of a right triangle is called the hypotenuse.
- A Pythagorean Triple can only be found in a right triangle.
Vocabulary
| Term | Definition |
|---|---|
| Hypotenuse | The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle. |
| Legs of a Right Triangle | The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle. |
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle. |
| Pythagorean Triple | A Pythagorean Triple is a set of three whole numbers a,b and c that satisfy the Pythagorean Theorem, \(a^2+b^2=c^2\). |
| Right Triangle | A right triangle is a triangle with one 90 degree angle. |
Additional Resources
Video: Pythagorean Theorem 2
Practice: Basics of Pythagorean Theorem
Real World: Measuring the World

