4.26: Triangle Inequality Theorem
- Last updated
- Jun 15, 2022
- Save as PDF
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}Can any three lengths make a triangle? The answer is no. For example, the lengths 1, 2, 3 cannot make a triangle because 1+2=3, so they would all lie on the same line. The lengths 4, 5, 10 also cannot make a triangle because 4+5=9<10. Look at the pictures below:
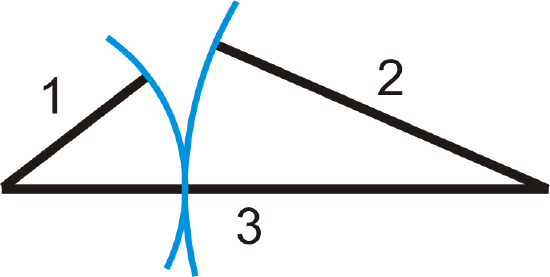
The arcs show that the two sides would never meet to form a triangle.
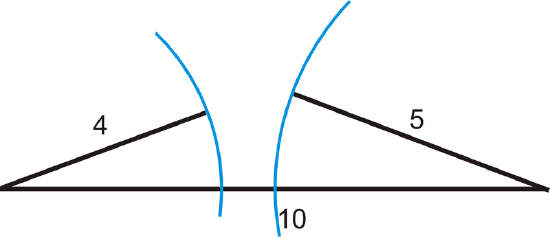
To make a triangle, two sides must add up to be greater than the third side. This is called the Triangle Inequality Theorem. This means that if you know two sides of a triangle, there are only certain lengths that the third side could be. If two sides have lengths a and b, then the length of the third side, s, has the range a−b<s<a+b.
What if you were given three lengths, like 5, 7 and 10? How could you determine if sides with these lengths form a triangle?
Example \PageIndex{1}
Do the lengths 4.1, 3.5, 7.5 make a triangle?
Solution
Use the Triangle Inequality Theorem. Check to make sure that the smaller two numbers add up to be greater than the largest number.
4.1+3.5>7.5 and 7.6>7.5 so yes these lengths make a triangle.
Example \PageIndex{2}
Do the lengths 4, 4, 8 make a triangle?
Solution
Use the Triangle Inequality Theorem. Check to make sure that the smaller two numbers add up to be greater than the largest number.
4+8=12 and 12>11 so yes these lengths make a triangle.
Example \PageIndex{3}
Do the lengths 4, 11, 8 make a triangle?
Solution
Use the Triangle Inequality Theorem. Check to make sure that the smaller two numbers add up to be greater than the largest number.
4+8=12 and 12>11 so yes these lengths make a triangle.
Example \PageIndex{4}
Find the length of the third side of a triangle if the other two sides are 10 and 6.
Solution
The Triangle Inequality Theorem can also help you find the range of the third side. The two given sides are 6 and 10. The third side, s, must be between 10−6=4 and 10+6=16. In other words, the range of values for s is 4<s<16.
Notice the range is no less than 4, and not equal to 4. The third side could be 4.1 because 4.1+6>10. For the same reason, s cannot be greater than 16, but it could 15.9, 10+6>15.9.
Example \PageIndex{5}
The base of an isosceles triangle has length 24. What can you say about the length of each leg?
Solution
To solve this problem, remember that an isosceles triangle has two congruent sides (the legs). We have to make sure that the sum of the lengths of the legs is greater than 24. In other words, if x is the length of a leg:
\begin{align*} x+x&>24 \\ 2x&>24 \\ x&>12\end{align*}
Each leg must have a length greater than 12.
Review
Determine if the sets of lengths below can make a triangle. If not, state why.
- 6, 6, 13
- 1, 2, 3
- 7, 8, 10
- 5, 4, 3
- 23, 56, 85
- 30, 40, 50
- 7, 8, 14
- 7, 8, 15
- 7, 8, 14.99
If two lengths of the sides of a triangle are given, determine the range of the length of the third side.
- 8 and 9
- 4 and 15
- 20 and 32
- 2 and 5
- 10 and 8
- x and 2x
- The legs of an isosceles triangle have a length of 12 each. What can you say about the length of the base?
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.7.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Triangle Inequality Theorem | The Triangle Inequality Theorem states that in order to make a triangle, two sides must add up to be greater than the third side. |
Additional Resources
Interactive Element
Video: Triangle Inequality Theorem
Activities: Triangle Inequality Theorem Discussion Questions
Study Aids: Inequalities in Triangles Study Guide
Practice: Triangle Inequality Theorem
Real World: Triangle Inequality Theorem
