4.25: Comparing Angles and Sides in Triangles
- Page ID
- 4822
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Inequality theorems and ordering angles and sides of triangles.
SAS and SSS Inequality Theorems
Look at the triangle below. The sides of the triangle are given. Can you determine which angle is the largest? The largest angle will be opposite 18 because that is the longest side. Similarly, the smallest angle will be opposite 7, which is the shortest side.
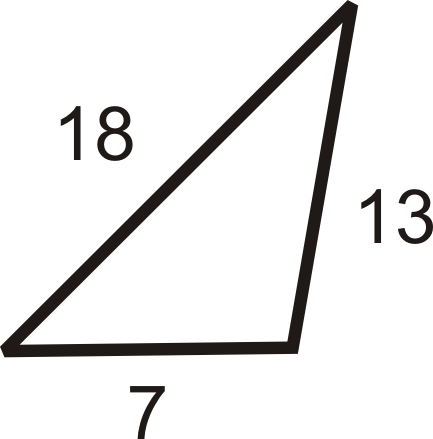
This idea is actually a theorem: If one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side.
The converse is also true: If one angle in a triangle is larger than another angle in that triangle, then the side opposite the larger angle will be longer than the side opposite the smaller angle.
We can extend this idea into two theorems that help us compare sides and angles in two triangles If we have two congruent triangles \(\Delta ABC\) and \(\Delta DEF\), marked below:
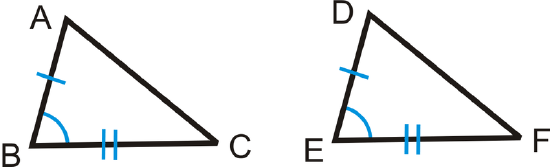
Therefore, if \(AB=DE\), \(BC=EF\), and \(m\angle B=m\angle E\), then \(AC=DF\).
Now, let’s make \(m\angle B>m\angle E\). Would that make \(AC>DF\)? Yes. This idea is called the SAS Inequality Theorem.
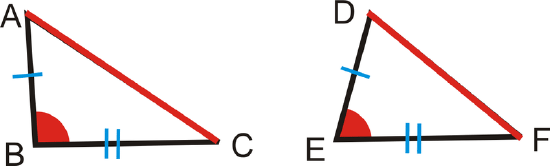
The SAS Inequality Theorem: If two sides of a triangle are congruent to two sides of another triangle, but the included angle of one triangle has greater measure than the included angle of the other triangle, then the third side of the first triangle is longer than the third side of the second triangle.

If \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) and \(m\angle B>m\angle E\), then \(\overline{AC}>\overline{DF}\).
If we know the third sides as opposed to the angles, the opposite idea is also true and is called the SSS Inequality Theorem.
SSS Inequality Theorem: If two sides of a triangle are congruent to two sides of another triangle, but the third side of the first triangle is longer than the third side of the second triangle, then the included angle of the first triangle's two congruent sides is greater in measure than the included angle of the second triangle's two congruent sides.

If \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) and \(\overline{AC}>\overline{DF}\), then\( m\angle B>m\angle E\).
What if you were told that a triangle has sides that measure 3, 4, and 5? How could you determine which of the triangle's angles is largest? Smallest?
Example \(\PageIndex{1}\)
If \(\overline{XM}\) is a median of \(\Delta XYZ\) and \(XY>XZ\), what can we say about \(m\angle 1\) and \(m\angle 2\)?
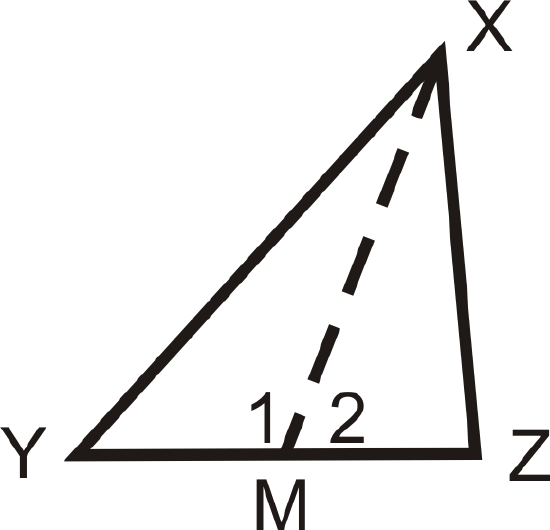
Solution
M is the midpoint of \(\overline{YZ}\), so \(YM=MZ\). \(MX=MX\) by the Reflexive Property and we know \(XY>XZ\).
We can use the SSS Inequality Theorem Converse to say \(m\angle 1>m\angle 2\).
Example \(\PageIndex{2}\)
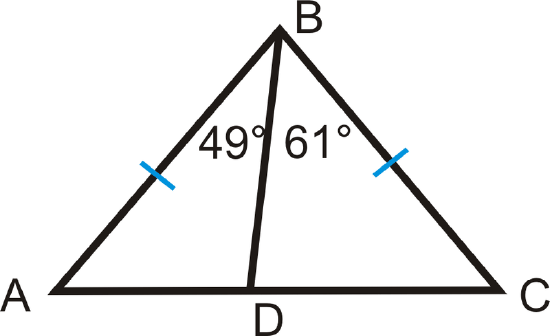
Below is isosceles triangle \(\Delta ABC\). List everything you can about the sides and angles of the triangle and why.
Solution
M is the midpoint of \(\overline{YZ}\), so \(YM=MZ\). \(MX=MX\) by the Reflexive Property and we know \(XY>XZ\).
\(AB=BC\) because it is given.
\(m\angle A=m\angle C\) because if sides are equal than their opposite angles must be equal..
\(AD<DC\) because \(m\angle ABD<m\angle CBD\) and because of the SAS Triangle Inequality Theorem.
Example \(\PageIndex{3}\)
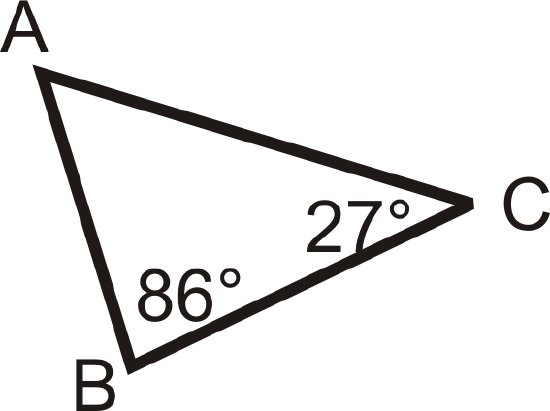
List the sides in order, from shortest to longest.
Solution
First, find m\angle A. From the Triangle Sum Theorem:
\(\begin{align*} m\angle A+86^{\circ}+27^{\circ}&=180^{\circ} \\ m\angle A&=67^{\circ} \end{align*}\)
\(86^{\circ}\) is the largest angle, so \(AC\) is the longest side. The next angle is \(67^{\circ}\), so \(BC\) would be the next longest side. \(27^{\circ}\) is the smallest angle, so \(AB\) is the shortest side. In order, the answer is: \(AB\), \(BC\), \(AC\).
Example \(\PageIndex{4}\)
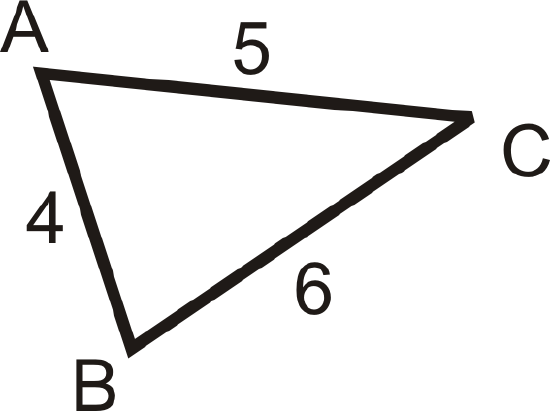
List the angles in order, from largest to smallest.
Solution
Just like with the sides, the largest angle is opposite the longest side. The longest side is \(BC\), so the largest angle is \(\angle A\). Next would be \(\angle B\) and then \(\angle C\).
Example \(\PageIndex{5}\)
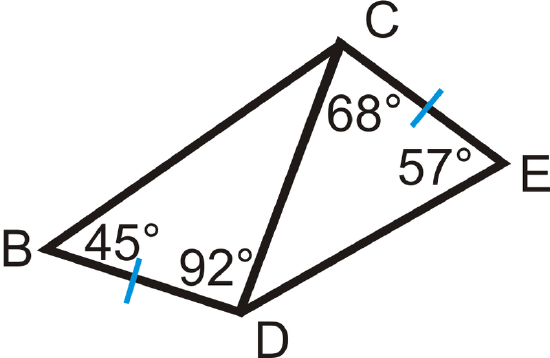
List the sides in order, from least to greatest.
Solution
To solve, let’s start with \Delta DCE\). The missing angle is \(55^{\circ}\). By the theorem presented in this section, the sides, in order from least to greatest are \(CE\), \(CD\), and \(DE\).
For \(\Delta BCD\), the missing angle is \(43^{\circ}\). Again, by the theorem presented in this section, the order of the sides from least to greatest is \(BD\), \(CD\), and \(BC\).
By the SAS Inequality Theorem, we know that \(BC>DE\), so the order of all the sides would be: \(BD\), \(CE\), \(CD\), \(DE\), \(BC\).
Review
For questions 1-3, list the sides in order from shortest to longest.
-
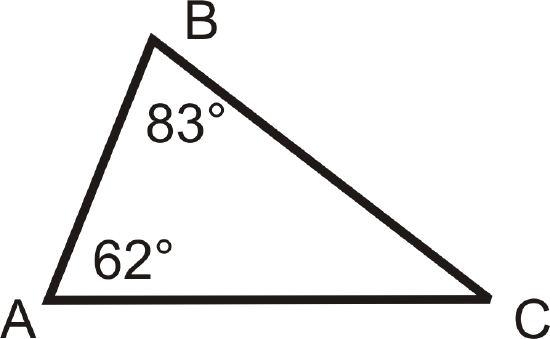
Figure \(\PageIndex{11}\) -
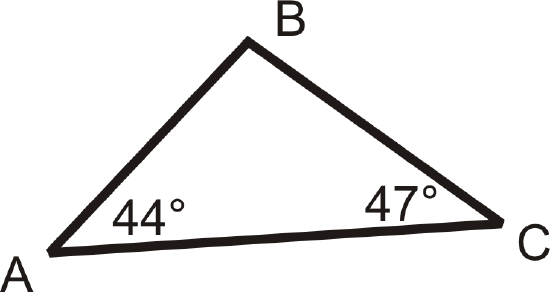
Figure \(\PageIndex{12}\) -
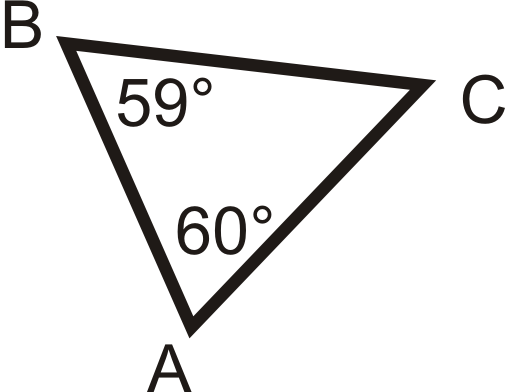
Figure \(\PageIndex{13}\)
For questions 4-6, list the angles from largest to smallest.
-
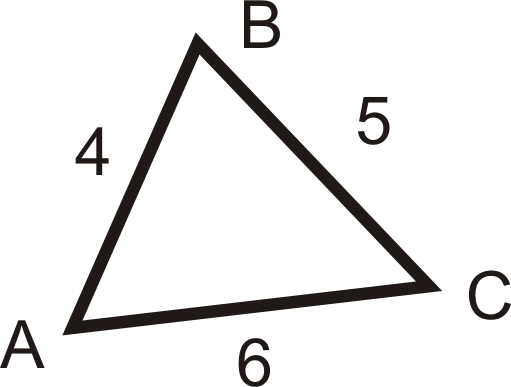
Figure \(\PageIndex{14}\) -
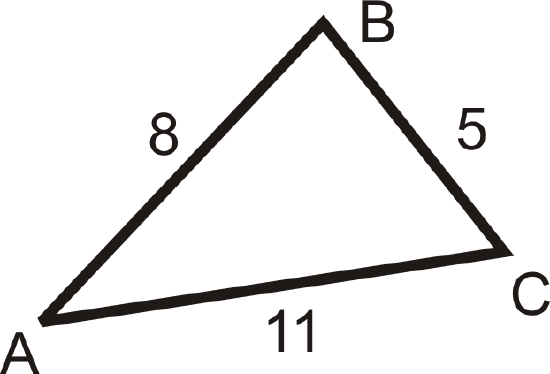
Figure \(\PageIndex{15}\) -
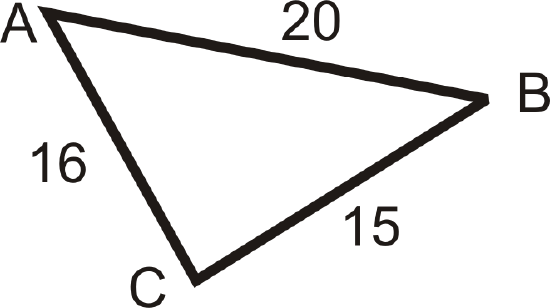
Figure \(\PageIndex{16}\) - Draw a triangle with sides 3 cm, 4 cm, and 5 cm. The angle measures are \(90^{\circ}\), \(53^{\circ}\), and \(37^{\circ}\). Place the angle measures in the appropriate spots.
- Draw a triangle with angle measures \(56^{\circ}\), \(54^{\circ}\) and the included side is 8 cm. What is the longest side of this triangle?
- Draw a triangle with sides 6 cm, 7 cm, and 8 cm. The angle measures are \(75.5^{\circ}\), \(58^{\circ}\), and \(46.5^{\circ}\). Place the angle measures in the appropriate spots.
- What conclusions can you draw about \(x\)?
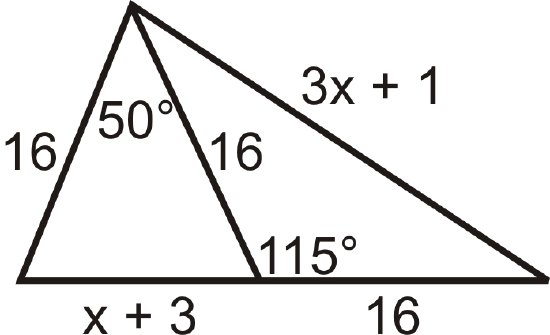
Figure \(\PageIndex{17}\) - Compare \(m\angle 1\) and \(m\angle 2\).
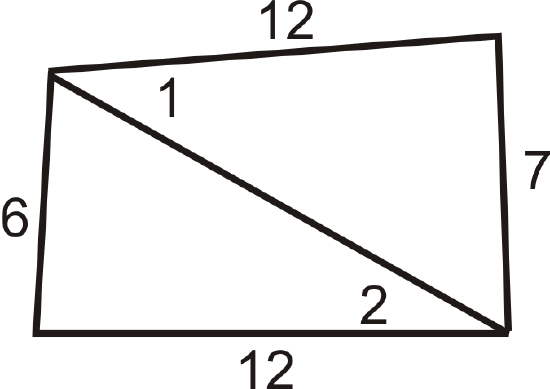
Figure \(\PageIndex{18}\) - List the sides from shortest to longest.
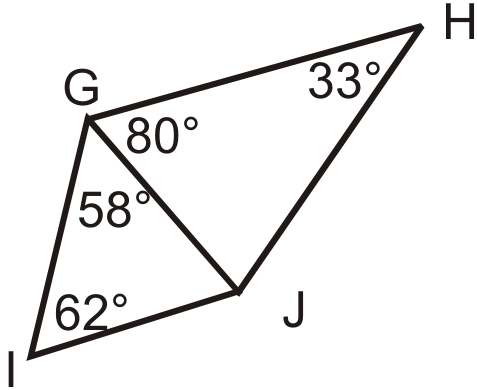
Figure \(\PageIndex{19}\) - Compare \(m\angle 1\) and \(m\angle 2\). What can you say about \(m\angle 3\) and \(m\angle 4\)?
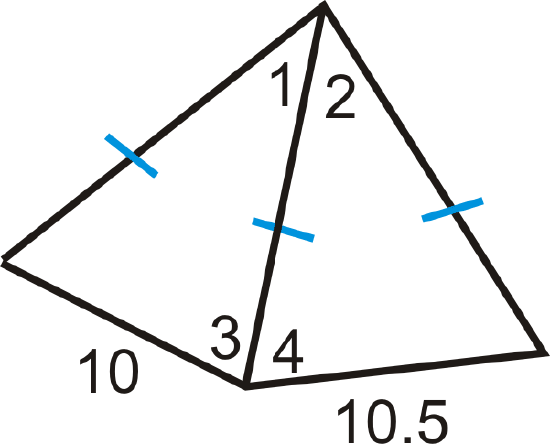
Figure \(\PageIndex{20}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.6.
Resources
Vocabulary
| Term | Definition |
|---|---|
| SAS Inequality Theorem | The SAS Inequality Theorem states that if two sides of a triangle are congruent to two sides of another triangle, but the included angle of one triangle has greater measure than the included angle of the other triangle, then the third side of the first triangle is longer than the third side of the second triangle. |
| SSS Inequality Theorem | The SSS Inequality Theorem states that if two sides of a triangle are congruent to two sides of another triangle, but the third side of the first triangle is longer than the third side of the second triangle, then the included angle of the first triangle's two congruent sides is greater in measure than the included angle of the second triangle's two congruent sides. |
| Triangle Sum Theorem | The Triangle Sum Theorem states that the three interior angles of any triangle add up to 180 degrees. |
Additional Resources
Interactive Element
Video: Comparing Angles & Sides in Triangles Principles - Basic
Activities: Comparing Angles and Sides in Triangles Discussion Questions
Study Aids: Inequalities in Triangles Study Guide
Practice: Comparing Angles and Sides in Triangles
Real World: Triangle Sum Theorem

