Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

4.24: Altitudes

Last updated

Jun 15, 2022
Save as PDF

Page ID: 4821

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Height of a triangle or the line segment from a vertex and perpendicular to the opposite side.

In a triangle, a line segment from a vertex and perpendicular to the opposite side is called an altitude. It is also called the height of a triangle. The red lines below are all altitudes.

f-d_b8d2c9c3d429a6cc41d6877fdda931b6508f1b86b1d4a1012d50eb08+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{1}$

When a triangle is a right triangle, the altitude, or height, is the leg. If the triangle is obtuse, then the altitude will be outside of the triangle. If the triangle is acute, then the altitude will be inside the triangle.

What if you were given one or more of a triangle's angle measures? How would you determine where the triangle's altitude would be found?

Example $\PageIndex{1}$

True or false: The altitudes of an obtuse triangle are inside the triangle.

Solution

Every triangle has three altitudes. For an obtuse triangle, at least one of the altitudes will be outside of the triangle, as shown in the picture at the beginning of this section.

Example $\PageIndex{2}$

Draw the altitude for the triangle shown.

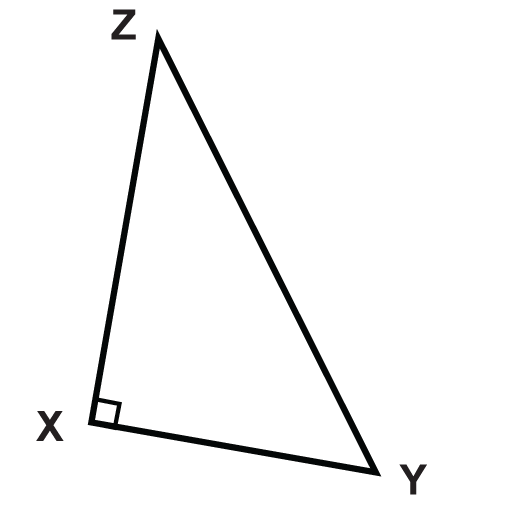
f-d_f3dd9812a401e27d7c3d5e98b7988fc2a4849ec73fec8c794102c585+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{2}$

Solution

The triangle is a right triangle, so the altitude is already drawn. The altitude is $\overline{XZ}$ .

Example $\PageIndex{3}$

Which line segment is the altitude of $\Delta ABC$ ?

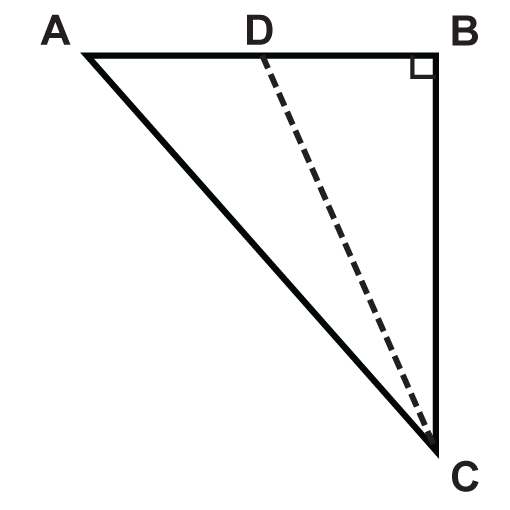
f-d_9ab359ff131f2f30902b71b6249388b55ec939f15006274f5dd38c69+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{3}$

Solution

In a right triangle, the altitude, or the height, is the leg. If we rotate the triangle so that the right angle is in the lower left corner, we see that leg $\overline{BC}$ is the altitude.

Example $\PageIndex{4}$

A triangle has angles that measure $55^{\circ}$ , $60^{\circ}$ , and $65^{\circ}$ . Where will the altitude be found?

Solution

Because all of the angle measures are less than $90^{\circ}$ , the triangle is an acute triangle. The altitude of any acute triangle is inside the triangle.

Example $\PageIndex{5}$

A triangle has an angle that measures $95^{\circ}$ . Where will an altitude be found?

Solution

Because $95^{\circ}>90^{\circ}$ , the triangle is obtuse and it will be outside the triangle.

Review

Given the following triangles, tell whether the altitude is inside the triangle, outside the triangle, or at the leg of the triangle.

Figure $\PageIndex{4}$
Figure $\PageIndex{5}$
Figure $\PageIndex{6}$
Figure $\PageIndex{7}$
Figure $\PageIndex{8}$
$\Delta JKL$ is an equiangular triangle.
$\Delta MNO$ is a triangle in which two the angles measure $30^{\circ}$ and $60^{\circ}$ .
$\Delta PQR$ is an isosceles triangle in which two of the angles measure $25^{\circ}$ .
$\Delta STU$ is an isosceles triangle in which two angles measures $45^{\circ}$ .

Given the following triangles, which line segment is the altitude?

$\Delta ABC$

Figure $\PageIndex{9}$
$\Delta EGH$

Figure $\PageIndex{10}$
$\Delta IJK$

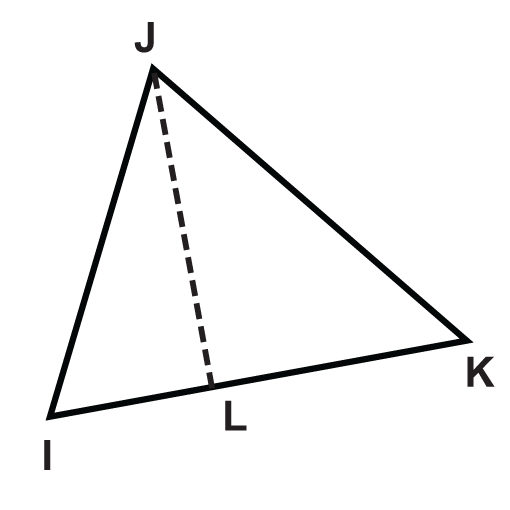
Figure $\PageIndex{11}$
$\Delta MNO$

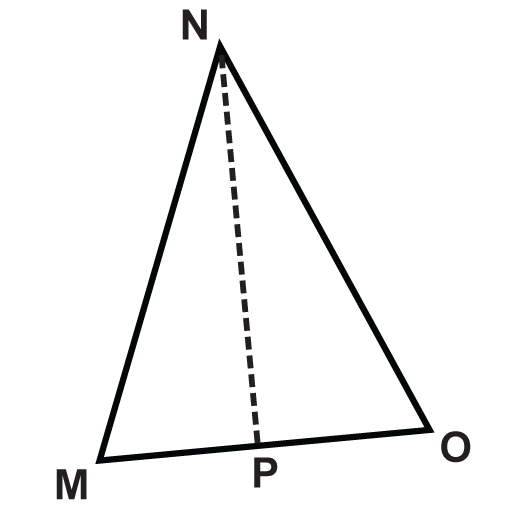
Figure $\PageIndex{12}$
$\Delta RSQ$

Figure $\PageIndex{13}$
$\Delta UVW$

Figure $\PageIndex{14}$

Resources

Review (Answers)

To see the Review answers, open this PDF file and look for section 5.5.

Vocabulary

Term	Definition
altitude	An altitude of a triangle is a line segment from a vertex and is perpendicular to the opposite side. It is also called the height of a triangle.

Additional Resources

Interactive Element

Video: Altitudes Principles - Basic

Activities: Altitudes Discussion Questions

Study Aids: Bisectors, Medians, Altitudes Study Guide

Real World: Altitudes