4.23: Medians
- Page ID
- 4820
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Line segment that joins a vertex and the midpoint of the opposite side of a triangle.
In a triangle, the line segment that joins a vertex and the midpoint of the opposite side is called a median.
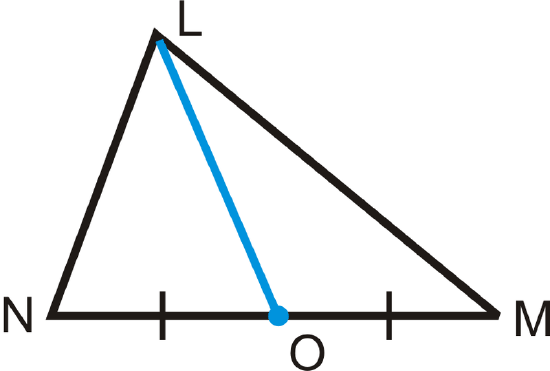
\overline{LO}\) is the median from L\) to the midpoint of \overline{NM}\).
If you draw all three medians they will intersect at one point called the centroid.
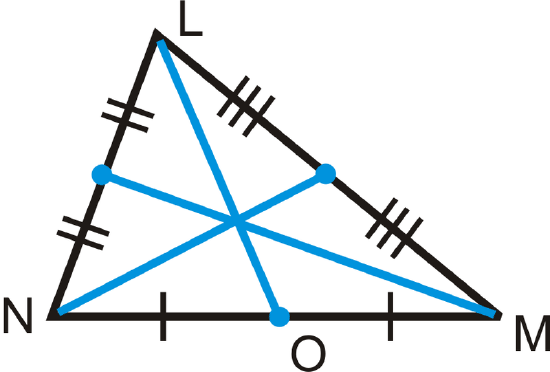
The centroid is the “balancing point” of a triangle. This means that if you were to cut out the triangle, the centroid is its center of gravity so you could balance it there.
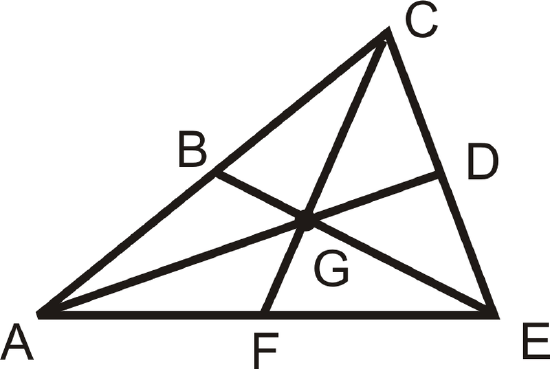
The Median Theorem states that the medians of a triangle intersect at a point called the centroid that is two-thirds of the distance from the vertices to the midpoint of the opposite sides.
So if \(G\) is the centroid, then:
\(AG=\dfrac{2}{3} AD, CG=\dfrac{2}{3} CF,\:EG=\dfrac{2}{3} BE\)
\(DG=\dfrac{1}{3} AD, FG=\dfrac{1}{3} CF,\:BG=\dfrac{1}{3} BE\)
\(And\: by \:substitution:DG =\dfrac{1}{2} AG,\:FG=\dfrac{1}{2} CG,\:BG=\dfrac{1}{2} EG\)
Example \(\PageIndex{1}\)
\(B\), \(D\), and \(F\) are the midpoints of each side and \(G\) is the centroid. If \(CG=16\), find \(GF\) and \(CF\).
Solution
Use the Median Theorem.
\(\begin{align*} CG&=\dfrac{2}{3} CF \\ 16&=\dfrac{2}{3} CF \\ CF&=24.\end{align*}\)
Therefore, \(GF=8\).
Example \(\PageIndex{2}\)
True or false: The median bisects the side it intersects.
Solution
This statement is true. By definition, a median intersects a side of a triangle at its midpoint. Midpoints divide segments into two equal parts.
Example \(\PageIndex{3}\)
\(I\), \(K\), and \(M\) are midpoints of the sides of \(\Delta HJL\).
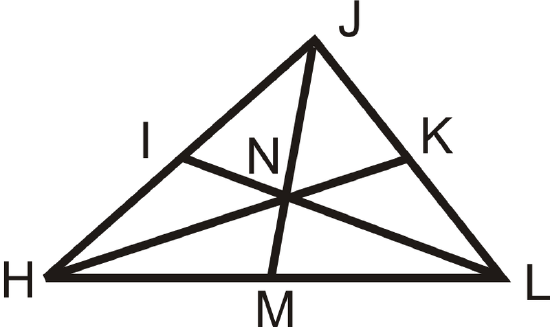
Solution
If \(JM=18\), find \(JN\) and \(NM\). If \(HN=14\), find \(NK\) and \(HK\).
Use the Median Theorem.
\(JN=\dfrac{2}{3} \cdot 18=12. NM=JM−JN=18−12\). \(NM=6\).
\(14=\dfrac{2}{3} \cdot HK\)
\(14\cdot \dfrac{3}{2} =HK=21\). \(NK\) is a third of 21, \(NK=7\).
Example \(\PageIndex{4}\)
H is the centroid of \(\Delta ABC\) and \(DC=5y−16\). Find \(x\) and \(y\).
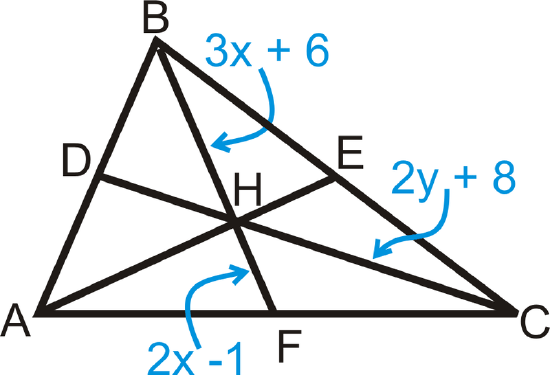
Solution
To solve, use the Median Theorem. Set up and solve equations.
\(\begin{align*} \dfrac{1}{2} BH=HF &\rightarrow BH=2HF &\qquad HC=\dfrac{2}{3} DC &\rightarrow \dfrac{3}{2} HC=DC \\ 3x+6&=2(2x−1) &\qquad \dfrac{3}{2} (2y+8)&=5y−16\\ 3x+6&=4x−2 &\qquad 3y+12 &=5y−16 \\ 8&=x &\qquad 28&=2y\rightarrow 14=y\end{align*} \)
Example \(\PageIndex{5}\)
\(B\), \(D\), and \(F\) are the midpoints of each side and G is the centroid. If \(BG=5\), find \(GE\) and \(BE\)
Solution
Use the Median Theorem.
\(\begin{align*} BG&=\dfrac{1}{3} BE \\ 5&=\dfrac{1}{3} BE \\ BE&=15.\end{align*}\)
Therefore, \(GE=10\).
Review
For questions 1-4, \(B\), \(D\), and \(F\) are the midpoints of each side and \(G\) is the centroid. Find the following lengths.
- If \(CG=16\), find \(GF\) and \(CF\)
- If \(AD=30\), find \(AG\) and \(GD\)
- If \(GF=x\), find \(GC\) and \(CF\)
- If \(AG=9x\) and \(GD=5x−1\), find \(x\) and \(AD\).
Multi-step Problems Find the equation of a median in the x−y\) plane.
- Plot \(\Delta ABC:\:A(−6,4)\),\:B(−2,4)\)\:and\:C(6,−4)\)
- Find the midpoint of \(\overline{AC}\). Label it \(D\).
- Find the slope of \(\overline{BD}\).
- Find the equation of \(\overline{BD}\).
- Plot \(\Delta DEF:\: D(−1,5),\:E(1,0),\:F(6,3)\)
- Find the midpoint of \(\overline{EF}\). Label it \(G\).
- Find the slope of \(\overline{DG}\).
- Find the equation of \\(overline{DG}\).
Determine whether the following statement is true or false.
- The centroid is the balancing point of a triangle.
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.4.
Resources
Vocabulary
| Term | Definition |
|---|---|
| centroid | The centroid is the point of intersection of the medians in a triangle. |
| Median | The median of a triangle is the line segment that connects a vertex to the opposite side's midpoint. |
Additional Resources
Interactive Element
Video: The Medians of a Triangle
Activities: Medians Discussion Questions
Study Aids: Bisectors, Medians, Altitudes Study Guide
Real World: Medians