4.22: Concurrence and Constructions
- Page ID
- 4819
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Constructions related to theorems involving circumcenters and other intersection points of three or more lines.
Given a triangle, what's the difference between the inscribed circle of the triangle and the circumscribed circle of the triangle?
Inscribed and Circumscribed Circles of Triangles
Given a triangle, an inscribed circle is the largest circle contained within the triangle. The inscribed circle will touch each of the three sides of the triangle in exactly one point. The center of the circle inscribed in a triangle is the incenter of the triangle, the point where the angle bisectors of the triangle meet.
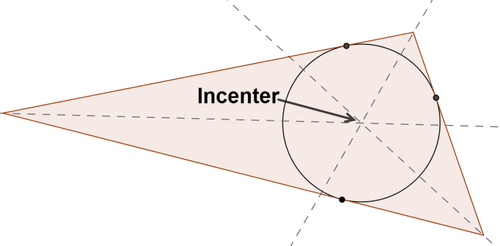
To construct the inscribed circle:
- Construct the incenter.
- Construct a line perpendicular to one side of the triangle that passes through the incenter. The segment connecting the incenter with the point of intersection of the triangle and the perpendicular line is the radius of the circle.
- Construct a circle centered at the incenter with the radius found in step 2.
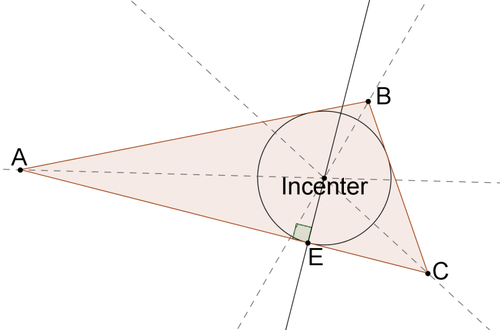
The steps for constructing the inscribed circle for a given triangle will be explored in the problems below.
Given a triangle, the circumscribed circle is the circle that passes through all three vertices of the triangle. The center of the circumscribed circle is the circumcenter of the triangle, the point where the perpendicular bisectors of the sides meet.
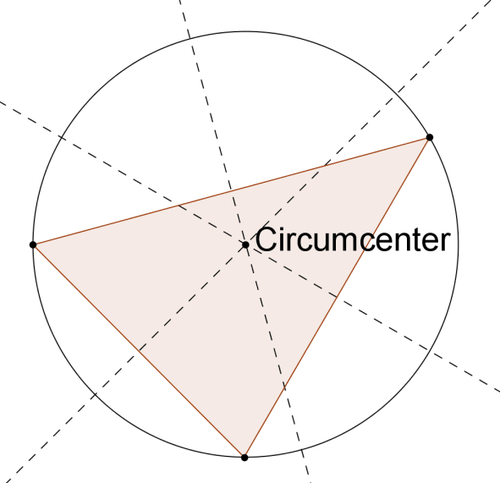
To construct the circumscribed circle:
- Construct the circumcenter.
- Construct a circle centered at the circumcenter that passes through one of the vertices. This same circle should pass through all three vertices.
The steps for constructing the circumscribed circle for a given triangle will be explored in the Examples section.
Constructing Angle Bisectors
Draw a triangle. Construct the angle bisectors of two of its angles. Why is the point of intersection of the two angle bisectors the incenter of the circle?
Use your compass and straightedge to construct the angle bisector of one of the angles.
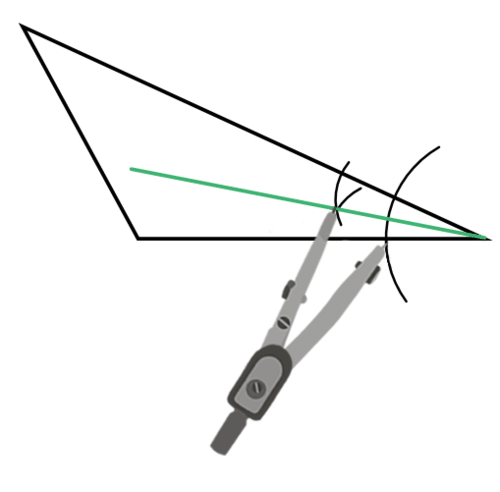
Repeat with a second angle.
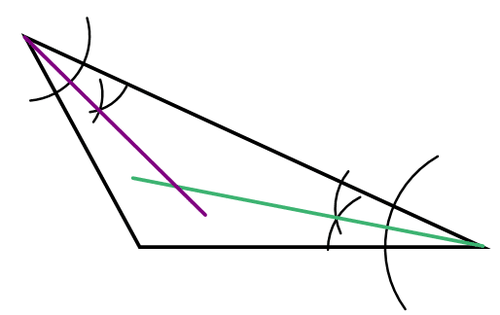
The point of intersection of the angle bisectors is the incenter. It is not necessary to construct all three angle bisectors because they all meet in the same point. The third angle bisector does not provide any new information.
Constructing Perpendicular Lines
Construct a line perpendicular to one side of the triangle that passes through the incenter of the triangle.
Use your compass and straightedge to construct a line perpendicular to one side of the triangle that passes through the incenter.
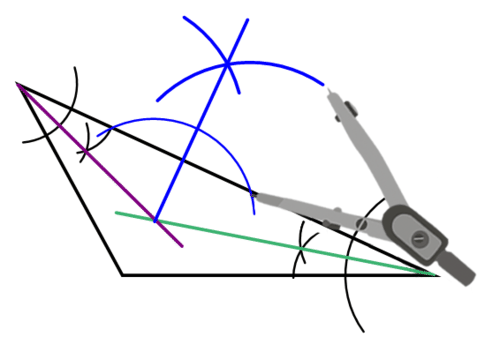
Constructing Inscribed Circles
Construct a circle centered at the incenter that passes through the point of intersection of the side of the triangle and the perpendicular line from the problem above.
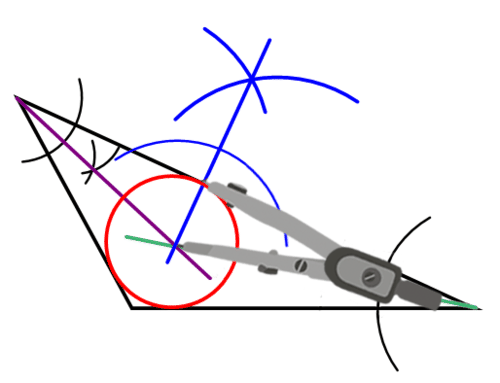
Note that this circle touches each side of the triangle exactly once.
Example \(\PageIndex{1}\)
Earlier, you were asked what is the difference between the inscribed circle of the triangle and the circumscribed circle of the triangle.
Solution
The inscribed circle of a triangle is inside the triangle. The circumscribed circle of a triangle is outside the triangle.
Example \(\PageIndex{2}\)
Draw a triangle. Construct the perpendicular bisectors of two of its sides. Why is the point of intersection of the two perpendicular bisectors the circumcenter of the circle?
Solution
Use your compass and straightedge to construct the perpendicular bisector of one side.
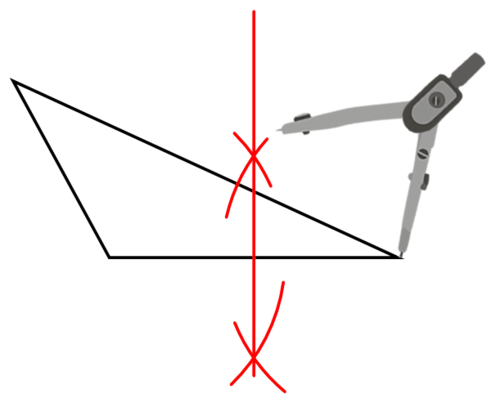
Repeat with a second side.
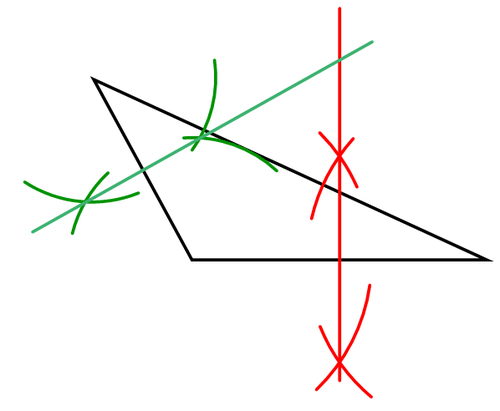
The point of intersection of the perpendicular bisectors is the circumcenter. It is not necessary to construct all three perpendicular bisectors because they all meet in the same point. The third perpendicular bisector does not provide any new information.
Example \(\PageIndex{3}\)
Continue with your triangle from #2. Construct the circumscribed circle of the triangle.
Solution
Construct a circle centered at the circumcenter that passes through one of the vertices of the triangle. This circle should pass through all three vertices.
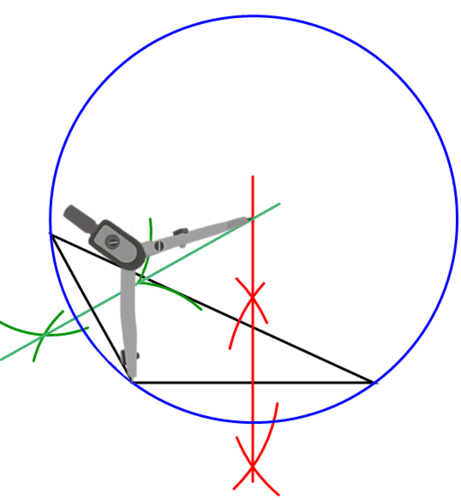
Example \(\PageIndex{4}\)
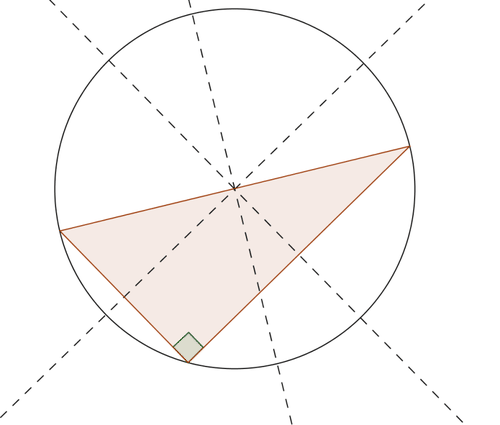
Justify the statement: The hypotenuse of a right triangle will be a diameter of the circumscribed circle of the triangle.
Solution
Each of the angles that make up a triangle become inscribed angles of the circumscribed circle. A \(90^{\circ}\) angle will intercept an arc of \(180^{\circ}\), which is half a circle. Therefore, the side opposite the \(90^{\circ}\) angle of the triangle must be a diameter of the circle.
Review
1. Draw a triangle and construct the angle bisector of two of its angles.
2. Continue with your triangle from #1. Construct a line perpendicular to one side of the triangle that passes through the incenter of the triangle.
3. Continue with your triangle from #1 and #2. Construct the inscribed circle of the triangle.
4. Why was it not necessary to construct the angle bisector of all three of the angles of the triangle?
5. Explain why the incenter is equidistant from each of the sides of the triangle.
6. Draw a triangle and construct the perpendicular bisector of two of its sides.
7. Continue with your triangle from #5. Construct the circumscribed circle of the triangle.
8. Explain why the circumcenter is equidistant from each of the vertices of the triangle.
You work selling food from a food truck at a local park. You want to position your truck so that it is the same distance away from each of the three locations shown on the map below.

9. Is the point of interest the incenter or the circumcenter?
10. Find the point on the map that is equidistant from each of the three locations.
11. How could you fold the map in two places to find the point equidistant from each of the three locations?
A new elementary school is to be constructed in your town. The plan is to build the school so that it is the same distance away from each of the three major roads shown in the map below.
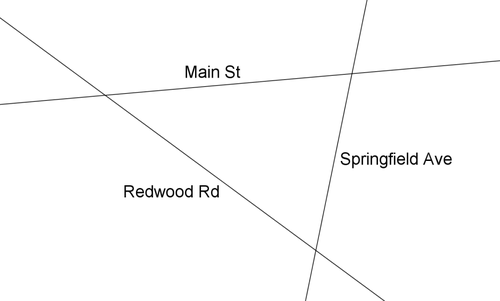
12. Is the point of interest the incenter or the circumcenter?
13. Find the point on the map that is equidistant from each of the three roads.
14. How could you fold the map in two places to find the point equidistant from each of the three roads?
15. Justify the following statement: Given any three non-collinear points, there exists exactly one circle that passes through the points.
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.5.
Vocabulary
| Term | Definition |
|---|---|
| perpendicular bisector | A perpendicular bisector of a line segment passes through the midpoint of the line segment and intersects the line segment at \(90^{\circ}\). |
| Inscribed Circle of a Triangle | The largest circle contained within the triangle. The inscribed circle will just touch each of the three sides of the triangle (it is tangent to each of the three sides of the triangle). |
Additional Resources
Interactive Element

