2.5.1: Radian Measure
- Page ID
- 4233
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
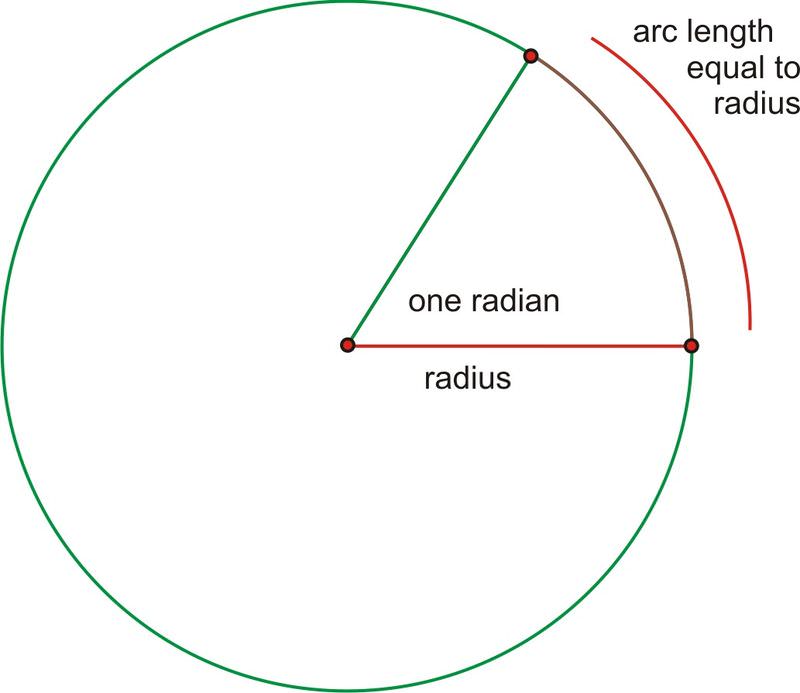
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angle measure in a circle where the arc length equals the radius.
While working on an experiment in your school science lab, your teacher asks you to turn up a detector by rotating the knob \(\dfrac{\pi}{2}\) radians. You are immediately puzzled, since you don't know what a radian measure is or how far to turn the knob.
Measure of Radians
Until now, we have used degrees to measure angles. But, what exactly is a degree? A degree is \(\dfrac{1}{360^{th}}\) of a complete rotation around a circle. Radians are alternate units used to measure angles in trigonometry. Just as it sounds, a radian is based on the radius of a circle. One radian (abbreviated rad) is the angle created by bending the radius length around the arc of a circle. Because a radian is based on an actual part of the circle rather than an arbitrary division, it is a much more natural unit of angle measure for upper level mathematics.
What if we were to rotate all the way around the circle? Continuing to add radius lengths, we find that it takes a little more than 6 of them to complete the rotation.
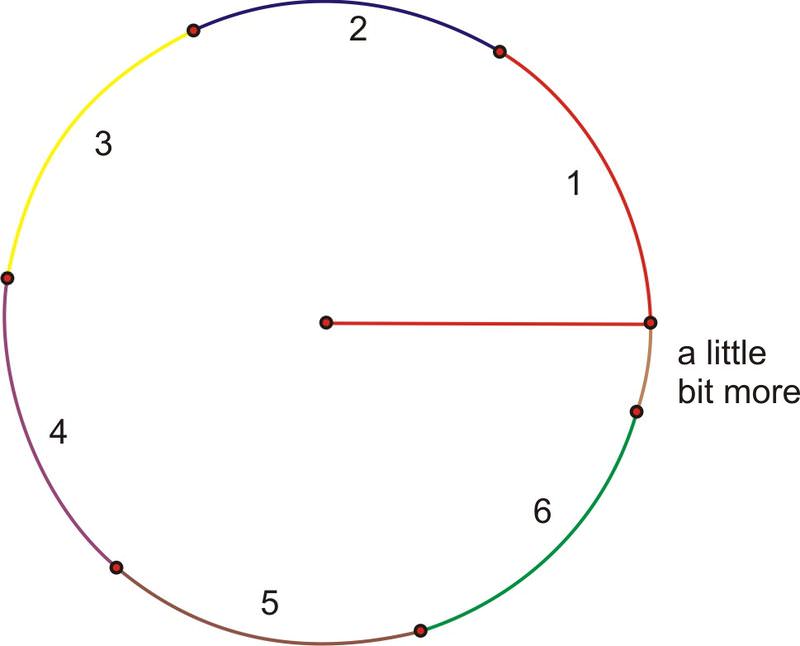
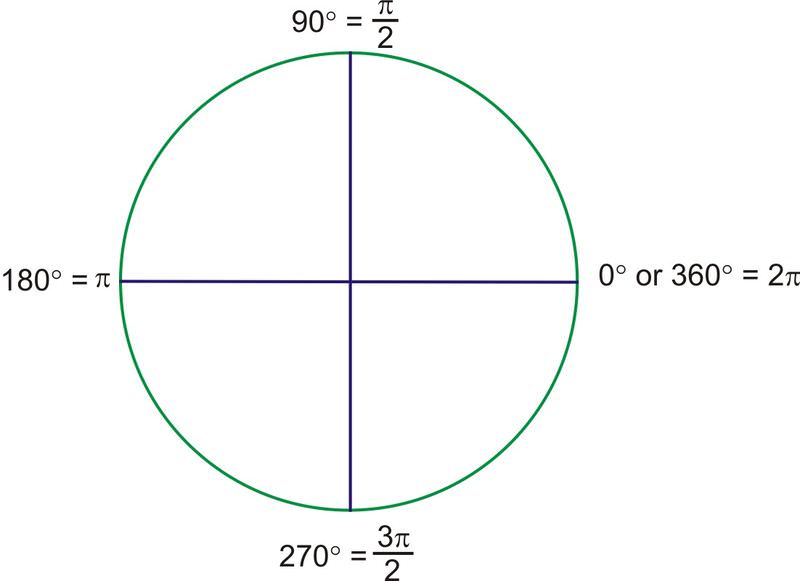
Recall from geometry that the arc length of a complete rotation is the circumference, where the formula is equal to \(2\pi\) times the length of the radius. \(2\pi\) is approximately 6.28, so the circumference is a little more than 6 radius lengths. Or, in terms of radian measure, a complete rotation (360 degrees) is \(2\pi\) radians.
\(360\text{ degrees}=2\pi \text{ radians}\)
With this as our starting point, we can find the radian measure of other angles. Half of a rotation, or 180 degrees, must therefore be \(\pi\) radians, and 90 degrees must be \(\dfrac{1}{2}\pi\), written \(\dfrac{\pi}{2}\).
Extending the radian measure past the first quadrant, the quadrantal angles have been determined, except \(270^{\circ} \). Because \(270^{\circ}\) is halfway between \(180^{\circ} \) (\(\pi\)) and \(360^{\circ} \) (\(2\pi\)), it must be \(1.5\pi\), usually written \(\dfrac{3\pi}{2}\).
For the \(45^{\circ}\) angles, the radians are all multiples of \(\dfrac{\pi}{4}\).
For example, \(135^{\circ}\) is \(3\cdot 45^{\circ}\). Therefore, the radian measure should be \(3\cdot \dfrac{\pi}{4}\), or \(\dfrac{3\pi}{4}\). Here are the rest of the multiples of \(45^{\circ}\),in radians:
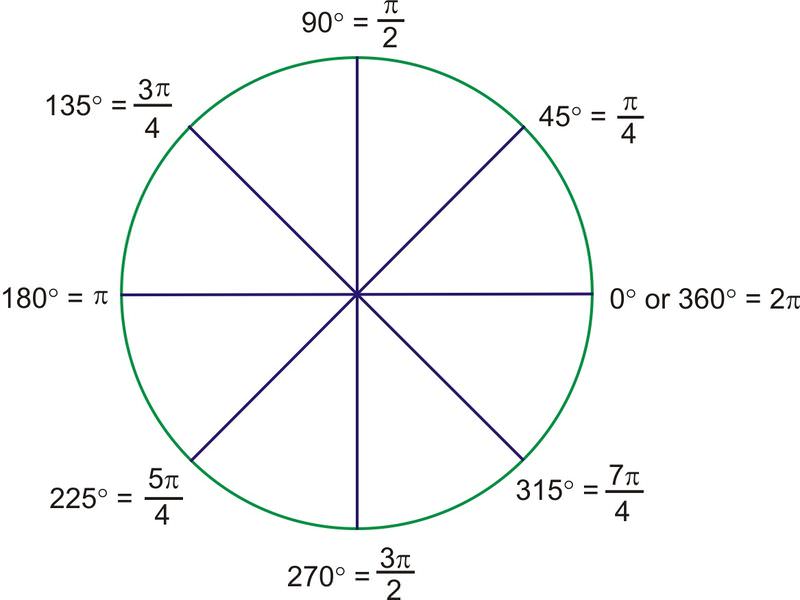
Notice that the additional angles in the drawing all have reference angles of 45 degrees and their radian measures are all multiples of \(\dfrac{\pi}{4}\). All of the even multiples are the quadrantal angles and are reduced, just like any other fraction.
Let's do some problems that involve radian measures.
1. Find the radian measure of these angles.
| Angle in Degrees | Angle in Radians |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | |
| 30 |
Because 45 is half of 90, half of \(\dfrac{1}{2}\pi\) is \(\dfrac{1}{4}\pi\). 30 is one-third of a right angle, so multiplying gives:
\(\dfrac{\pi}{2}\times \dfrac{1}{3}=\dfrac{\pi}{6}\)
and because 60 is twice as large as 30:
\(2\times \dfrac{\pi}{6}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\)
Here is the completed table:
| Angle in Degrees | Angle in Radians |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | \(\dfrac{\pi}{4}\) |
| 30 | \(\dfrac{\pi}{6}\) |
There is a formula to convert between radians and degrees that you may already have discovered while doing this example. However, many angles that are commonly used can be found easily from the values in this table. For example, most students find it easy to remember 30 and 60. 30 is \(\pi\) over 6 and 60 is \(\pi\) over 3. Knowing these angles, you can find any of the special angles that have reference angles of 30 and 60 because they will all have the same denominators. The same is true of multiples of \(\dfrac{\pi}{4}\) (45 degrees) and \(\dfrac{\pi}{2}\) (90 degrees).
2. Complete the following radian measures by counting in multiples of \(\dfrac{\pi}{3}\) and \(\dfrac{\pi}{6}\):
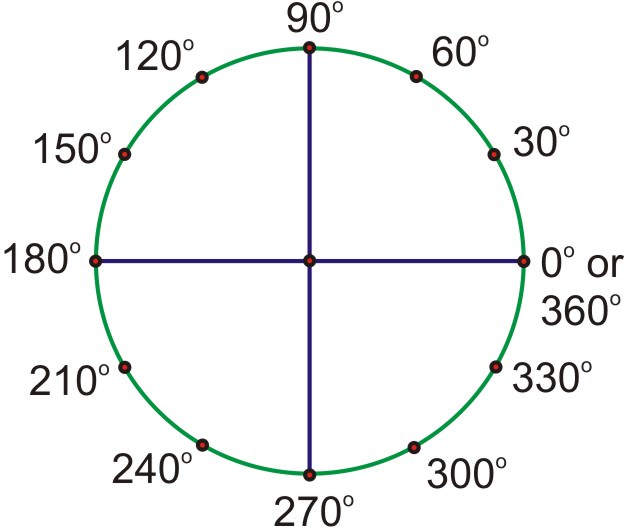

Notice that all of the angles with 60-degree reference angles are multiples of \(\dfrac{\pi}{3}\), and all of those with 30-degree reference angles are multiples of \(\dfrac{\pi}{6}\). Counting in these terms based on this pattern, rather than converting back to degrees, will help you better understand radians.
3. Find the radian measure of these angles.
| Angle in Degrees | Angle in Radians |
|---|---|
| 120 | \(\dfrac{2 \pi}{3}\) |
| 180 | |
| 240 | |
| 270 | |
| 300 |
Because 30 is one-third of a right angle, multiplying gives:
\(\dfrac{\pi}{2}\times 13=\dfrac{\pi}{6}\)
adding this to the known value for ninety degrees of \(\dfrac{\pi}{2}\):
\(\dfrac{\pi}{2}+\dfrac{\pi}{6}=3\dfrac{\pi}{6}+\dfrac{\pi}{6}=4\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\)
Here is the completed table:
| Angle in Degrees | Angle in Radians |
|---|---|
| 120 | \(\dfrac{2\pi}{3}\) |
| 180 | \(\pi\) |
| 240 | \(\dfrac{4\pi}{3}\) |
| 300 | \(\dfrac{5\pi}{3}\) |
Earlier, you were given a problem about rotating the knob.
Solution
Since \(45^{\circ} =\dfrac{\pi}{4} \text{ rad}\), then \(2\times \dfrac{\pi}{4}=\dfrac{\pi}{2}=2\times 45^{\circ}\). Therefore, a turn of \(\dfrac{\pi}{2}\) is equal to \(90^{\circ}\), which is \(\dfrac{1}{4}\) of a complete rotation of the knob.
Give the radian measure of \(60^{\circ}\)
Solution
30 is one-third of a right angle. This means that since \(90^{\circ} =\dfrac{\pi}{2}\), then \(30^{\circ} =\dfrac{\pi}{6}\). Therefore, multiplying gives:
\(\dfrac{\pi}{6}\times 2=\dfrac{\pi}{3}\)
Give the radian measure of \(75^{\circ}\)
Solution
15 is one-sixth of a right triangle. This means that since \(90^{\circ} =\dfrac{\pi}{2}\), then \(15^{\circ} =\dfrac{\pi}{12}\). Therefore, multiplying gives:
\(\dfrac{\pi}{12}\times 5=\dfrac{5\pi}{12}\)
Give the radian measure of \(180^{\circ}\)
Solution
Since \(90^{\circ} =\dfrac{\pi}{2}\), then \(180^{\circ} =\dfrac{2\pi}{2}=\pi\)
Review
Find the radian measure of each angle.
- \(90^{\circ}\)
- \(120^{\circ}\)
- \(300^{\circ}\)
- \(330^{\circ}\)
- \(−45^{\circ}\)
- \(135^{\circ}\)
Find the degree measure of each angle.
- \(\dfrac{3\pi}{2}\)
- \(\dfrac{5\pi}{4}\)
- \(\dfrac{7\pi}{6}\)
- \(\dfrac{\pi}{6}\)
- \(\dfrac{5\pi}{3}\)
- \(\pi\)
- Explain why if you are given an angle in degrees and you multiply it by \(\dfrac{\pi}{180}\) you will get the same angle in radians.
- Explain why if you are given an angle in radians and you multiply it by \(\dfrac{180}{\pi}\) you will get the same angle in degrees.
- Explain in your own words why it makes sense that there are \(2\pi\) radians in a circle.
Review (Answers)
To see the Review answers, open this PDF file and look for section 2.1.
Vocabulary
| Term | Definition |
|---|---|
| radian | A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius. |

