6.11: Arc Length
- Page ID
- 5026
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Portion of a circle's circumference.
One way to measure arcs is in degrees. This is called the “arc measure” or “degree measure” (see Arcs in Circles). Arcs can also be measured in length, as a portion of the circumference. Arc length is the length of an arc or a portion of a circle’s circumference. The arc length is directly related to the degree arc measure.
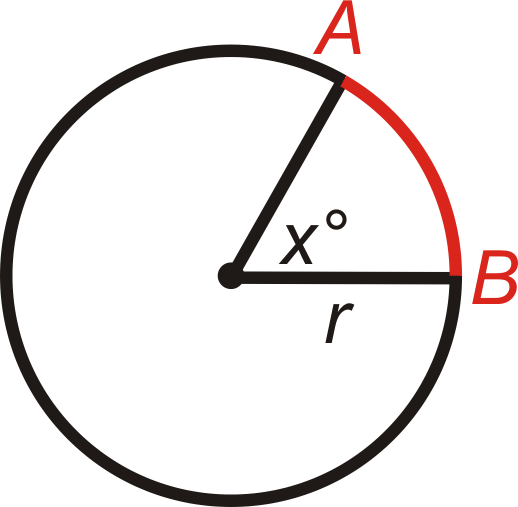
Arc Length Formula: The length of \(\widehat{AB}=\dfrac{m\widehat{AB}}{360^{\circ}}\cdot \pi d\) or \(\dfrac{m\widehat{AB}}{360^{\circ}}\cdot 2\pi r\).
What if you were given the angle measure of a circle's arc? How could you find the length of that arc?
Example \(\PageIndex{1}\)
Find the arc length of \(\widehat{PQ}\) in \(\bigodot A\). Leave your answers in terms of \(\pi\).
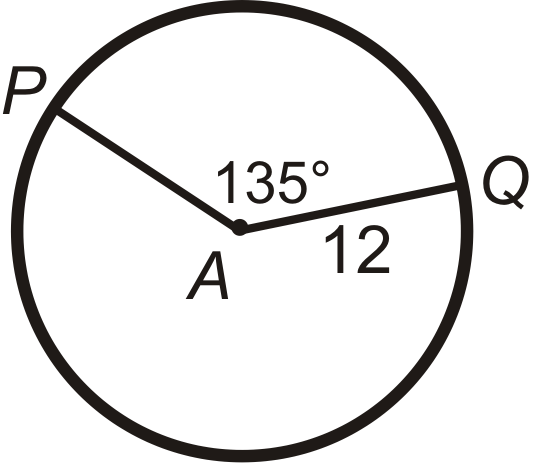
Solution
Use the Arc Length formula.
\(\begin{aligned} \widehat{PQ}&=\dfrac{135}{360}\cdot 2\pi (12) \\ \widehat{PQ}&=\dfrac{3}{8}\cdot 24\pi \\ \widehat{PQ}&=9\pi \end{aligned}\)
Example \(\PageIndex{2}\)
A typical large pizza has a diameter of 14 inches and is cut into 8 pieces. Think of the crust as the circumference of the pizza. Find the length of the crust for the entire pizza. Then, find the length of the crust for one piece of pizza if the entire pizza is cut into 8 pieces.

Solution
The entire length of the crust, or the circumference of the pizza, is \(14\pi \approx 44 in.\) In \(\dfrac{1}{8}\) of the pizza, one piece would have \(\dfrac{44}{8}\approx 5.5 inches\) of crust.
Example \(\PageIndex{3}\)
Find the length of \(\widehat{PQ}\). Leave your answer in terms of \(\pi\).
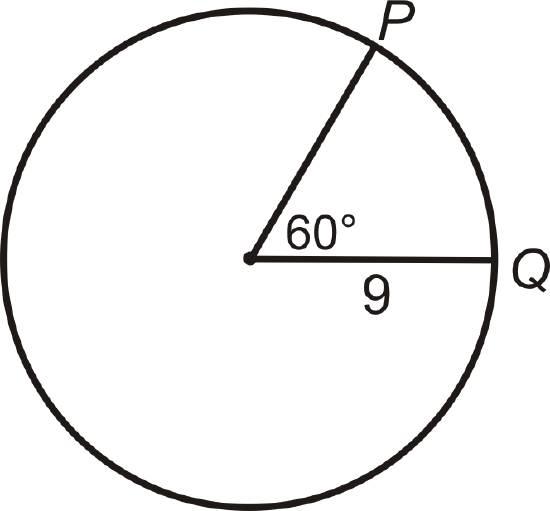
Solution
In the picture, the central angle that corresponds with \(\widehat{PQ}\) is \(60^{\circ}\). This means that \(m\widehat{PQ}=60^{\circ}\). Think of the arc length as a portion of the circumference. There are \(360^{\circ}\) in a circle, so 60^{\circ}\) would be 16 of that (\(60^{\circ}360^{\circ}=16\)). Therefore, the length of \(\widehat{PQ}\) is 16 of the circumference. \text{length of } \widehat{PQ}=16\cdot 2\pi (9)=3\pi \text{ units}\).
Example \(\PageIndex{4}\)
The arc length of a circle is \(\widehat{AB}=6\pi\) and is 14 the circumference. Find the radius of the circle.
Solution
If 6\pi is 14 the circumference, then the total circumference is \(4(6\pi )=24\pi\). To find the radius, plug this into the circumference formula and solve for r.
\(\begin{aligned} 24\pi =2\pi r \\ 12 \text{ units }=r \end{aligned}\)
Example \(\PageIndex{5}\)
Find the measure of the central angle or \(\widehat{PQ}\).
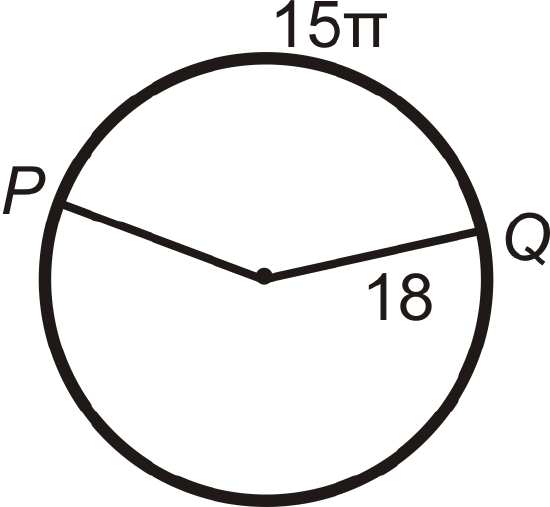
Solution
Let’s plug in what we know to the Arc Length Formula.
\(\begin{aligned}15\pi &=m\widehat{PQ}360^{\circ}\cdot 2\pi (18) \\ 15&=m\widehat{PQ}10^{\circ} \\ 150^{\circ}&=m\widehat{PQ}\end{aligned}\)
Review
Find the arc length of \(\widehat{PQ}\) in \(\bigodot A\). Leave your answers in terms of \(\pi\).
-
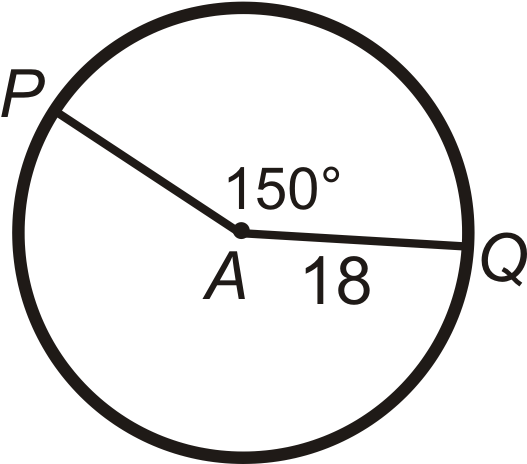
Figure \(\PageIndex{6}\) -
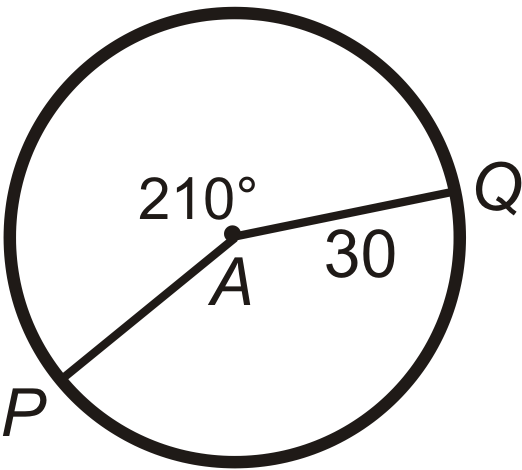
Figure \(\PageIndex{7}\) -
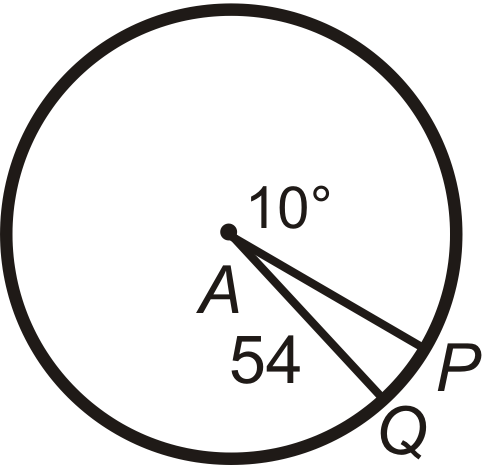
Figure \(\PageIndex{8}\) -
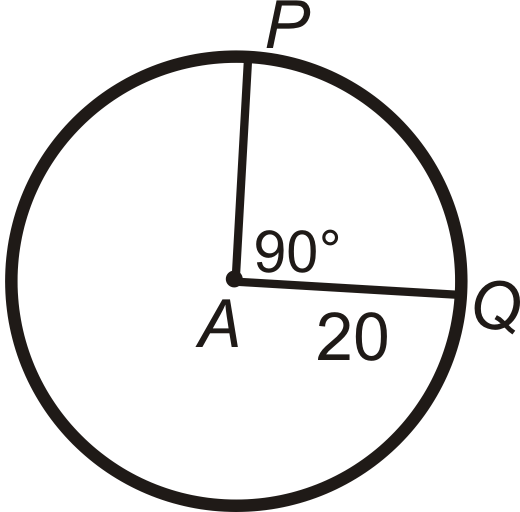
Figure \(\PageIndex{9}\)
Find \(PA\) (the radius) in \(\bigodot A\). Leave your answer in terms of \(\pi \).
-
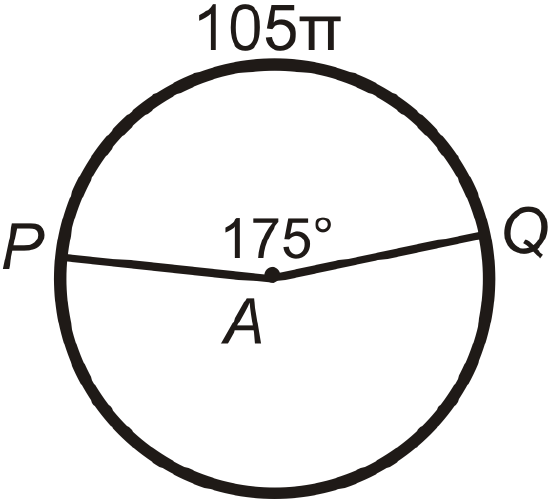
Figure \(\PageIndex{11}\) -
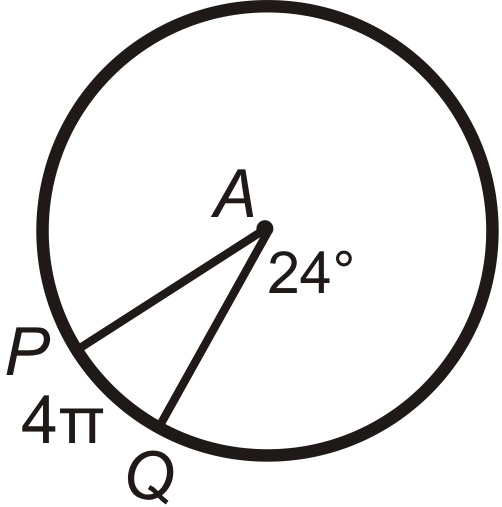
Figure \(\PageIndex{12}\) -
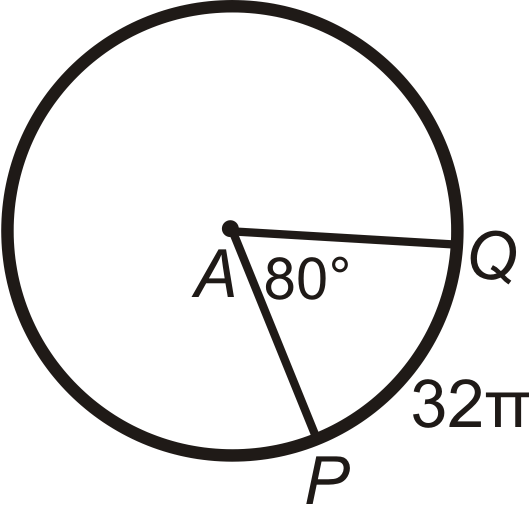
Figure \(\PageIndex{13}\)
Find the central angle or \(m\widehat{PQ}\) in \(\bigodot A\). Round any decimal answers to the nearest tenth.
-
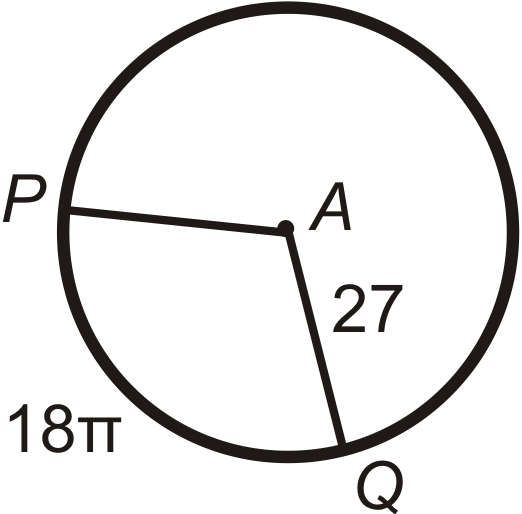
Figure \(\PageIndex{14}\) -
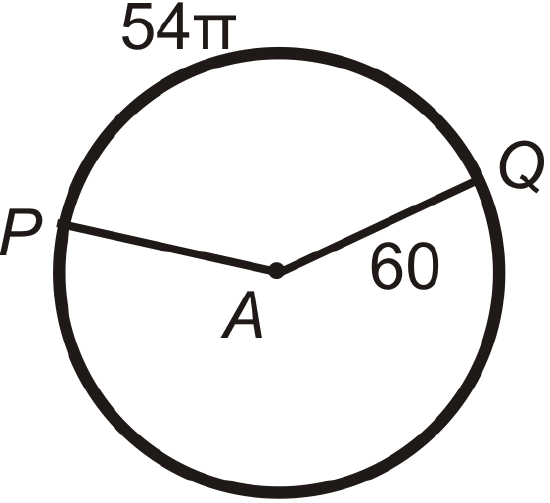
Figure \(\PageIndex{15}\) -
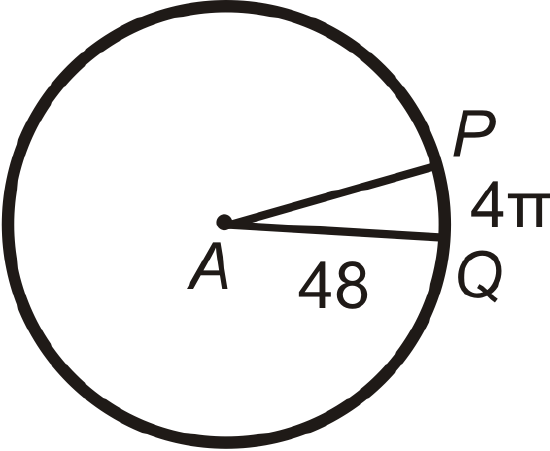
Figure \(\PageIndex{16}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.9.
Vocabulary
| Term | Definition |
|---|---|
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| pi | (or \(\pi\) ) The ratio of the circumference of a circle to its diameter. |
| radius | The distance from the center to the outer rim of a circle. |
| Arc | An arc is a section of the circumference of a circle. |
| arc length | In calculus, arc length is the length of a plane function curve over an interval. |
| Circumference | The circumference of a circle is the measure of the distance around the outside edge of a circle. |
| Dilation | To reduce or enlarge a figure according to a scale factor is a dilation. |
| radian | A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius. |
| Sector | A sector of a circle is a portion of a circle contained between two radii of the circle. Sectors can be measured in degrees. |
Additional Resources
Interactive Element
Video: Arc Length Principles - Basic
Activities: Arc Length Discussion Questions
Study Aids: Circumference and Arc Length Study Guide
Practice: Arc Length
Real World: How Far Is It to London?

