6.10: Area of Sectors and Segments
- Page ID
- 5025
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Area of parts of a circle.
Area of Sectors and Segments
A sector of a circle is the area bounded by two radii and the arc between the endpoints of the radii. If r is the radius and \widehat{AB} is the arc bounding a sector, then the area of the sector is \(A=\dfrac{m\widehat{AB} }{360^{\circ}}\cdot \pi r^2\).

A segment of a circle is the area of a circle that is bounded by a chord and the arc with the same endpoints as the chord. The area of a segment is \(A_{\text{segment}}=A_sector−A_{\Delta ABC}\)
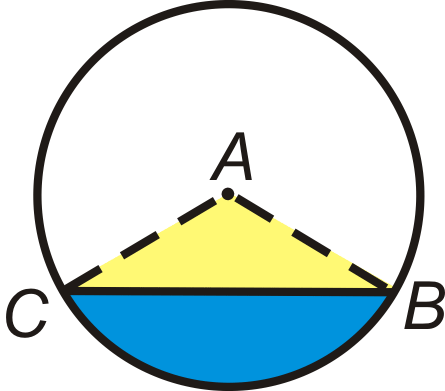
What if you were given a circle with two radii in which the region between those two radii was shaded? How could you find the area of that shaded region of the circle?
Example \(\PageIndex{1}\)
The area of a sector is \(135 \pi\) and the arc measure is 216^{\circ}. What is the radius of the circle?
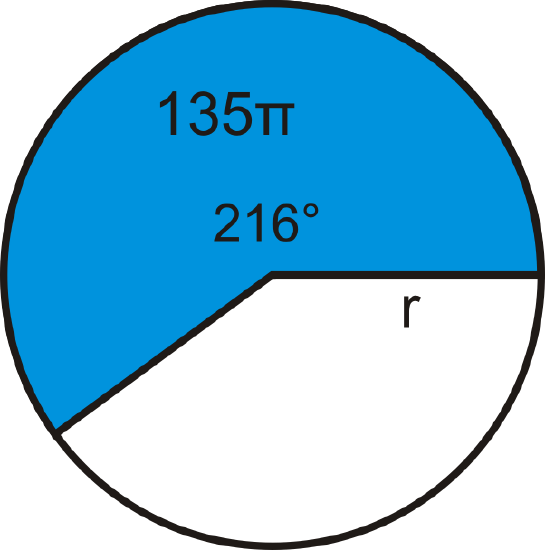
Solution
Plug in what you know to the sector area formula and solve for r.
\(\begin{aligned} 135 \pi &= \dfrac{216^{\circ}}{360^{\circ}}\cdot \pi r^2 \\ 135&=35\cdot r^2 \\ \dfrac{5}{3} \cdot 135 &=r^2 \\ 225 &=r^2 \rightarrow r=\sqrt{225}=15 \end{aligned}\)
Example \(\PageIndex{2}\)
Find the area of the shaded region. The quadrilateral is a square.
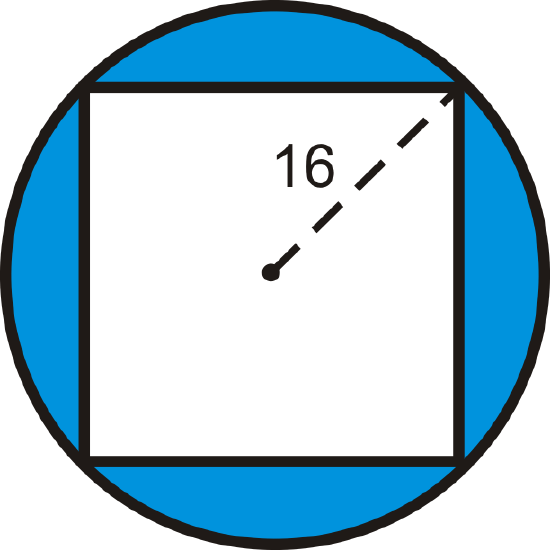
Solution
The radius of the circle is 16, which is also half of the diagonal of the square. So, the diagonal is 32 and the sides would be \dfrac{32}{\sqrt{2}}\cdot \dfrac{\sqrt{2}}{\sqrt{2}}=16\sqrt{2} because each half of a square is a 45-45-90 triangle.
\(\begin{aligned}A_{\text{circle}}&=16^2 \pi =256 \pi \\ A_{\text{square}}&=(16\sqrt{2})^2=256\cdot 2=512 \end{aligned}\)
The area of the shaded region is \(256 \pi −512 \approx 292.25\)
Example \(\PageIndex{3}\)
Find the area of the blue sector. Leave your answer in terms of \(\pi \).
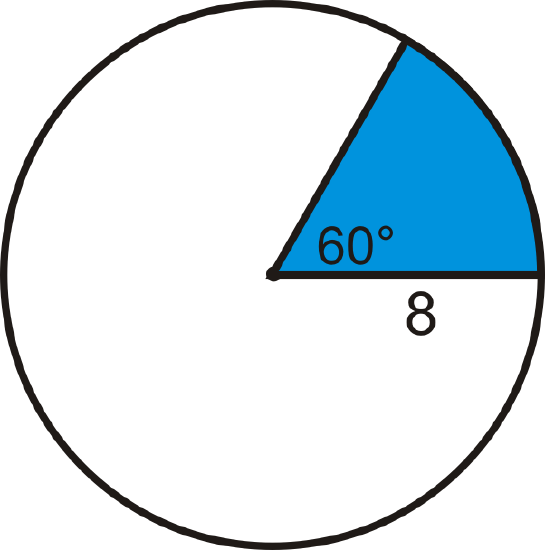
Solution
In the picture, the central angle that corresponds with the sector is \(60^{\circ}\). \(60^{\circ}\) is 16 of \(360^{\circ}\), so this sector is 16 of the total area. \(\text{area of blue sector }=16\cdot \pi 8^2=\dfrac{32}{3} \pi\)
Example \(\PageIndex{1}\)
The area of a sector is \(8 \pi\) and the radius of the circle is 12. What is the central angle?
Solution
Plug in what you know to the sector area formula and then solve for the central angle, which we will call x.
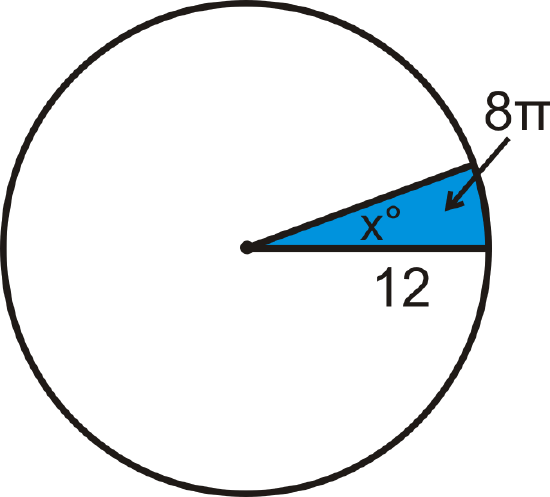
\(\begin{aligned}8 \pi &=\dfrac{x}{360^{\circ}}\cdot \pi 12^2 \\ 8 \pi &=\dfrac{x}{360^{\circ}}\cdot144 \pi \\ 8&=\dfrac{2x}{5^{\circ}} \\ x&=8\cdot \dfrac{5^{\circ}}{2}=20^{\circ} \end{aligned}\)
Example \(\PageIndex{1}\)
Find the area of the blue segment below.
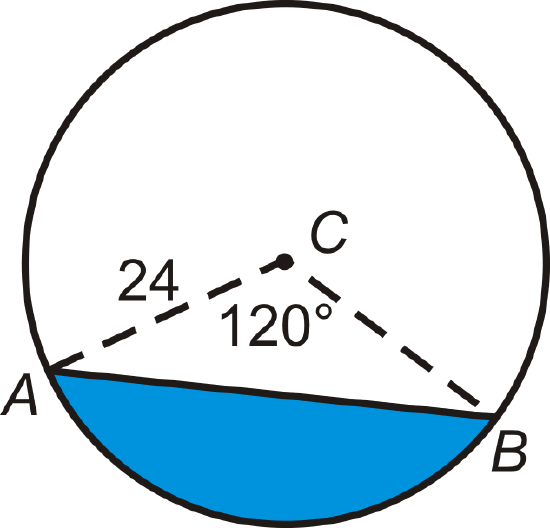
Solution
The area of the segment is the area of the sector minus the area of the isosceles triangle made by the radii. If we split the isosceles triangle in half, each half is a 30-60-90 triangle, where the radius is the hypotenuse. The height of \DeltaABC is 12 and the base is 2(123–√)=243–√.
\(\begin{array}{rlrl}
A_{\text {sector}} & =\frac{120}{360} \pi \cdot 24^{2} & A_{\triangle} & =\frac{1}{2}(24 \sqrt{3})(12) \\
& =192 \pi & & =144 \sqrt{3}
\end{array}\)
The area of the segment is \(A=192\pi−144\sqrt{3}\approx 353.8 \text{ units}\).
Review
Find the area of the blue sector or segment in ⨀A. Leave your answers in terms of \pi . Round any decimal answers to the nearest hundredth.
-
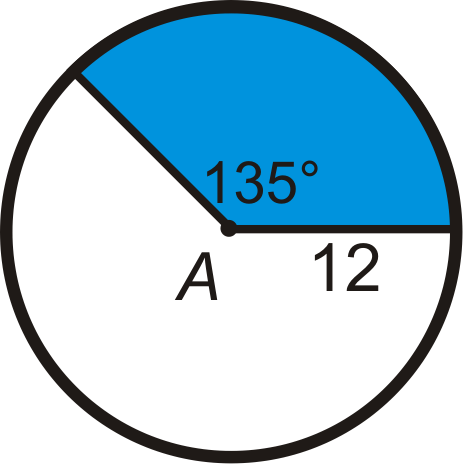
Figure \(\PageIndex{8}\) -
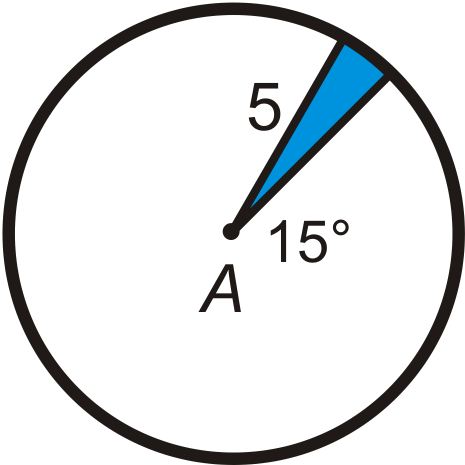
Figure \(\PageIndex{9}\) -
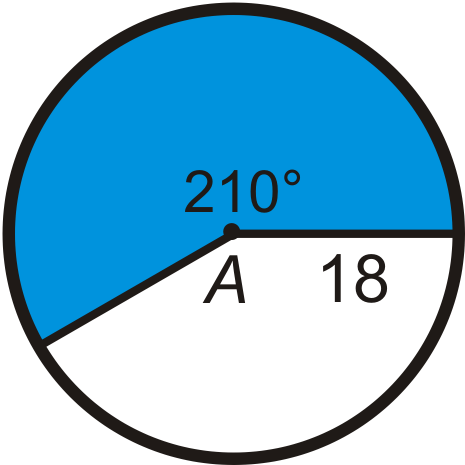
Figure \(\PageIndex{10}\) -
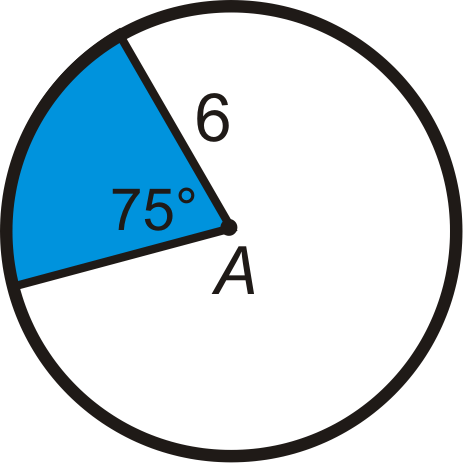
Figure \(\PageIndex{11}\) -
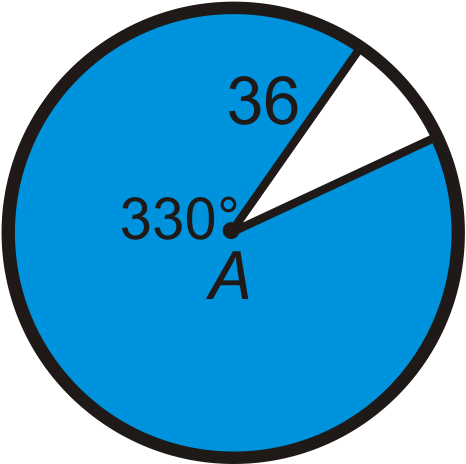
Figure \(\PageIndex{12}\)
Find the radius of the circle. Leave your answer in terms of \pi .
-
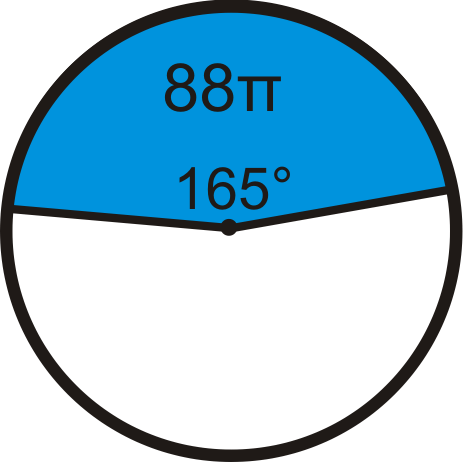
Figure \(\PageIndex{13}\) -
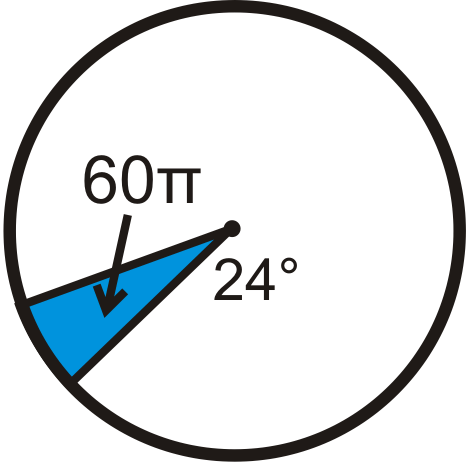
Figure \(\PageIndex{14}\) -
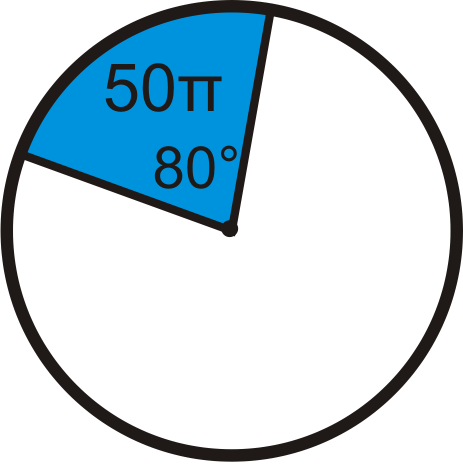
Figure \(\PageIndex{15}\)
Find the central angle of each blue sector. Round any decimal answers to the nearest tenth.
-
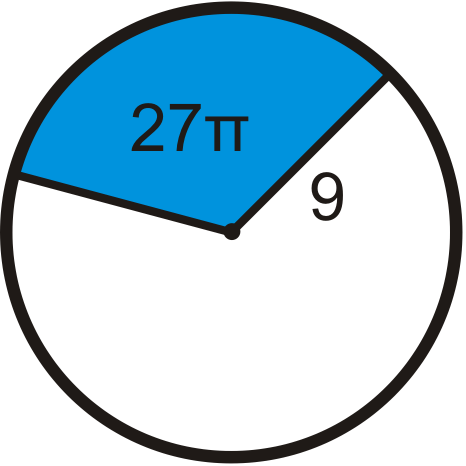
Figure \(\PageIndex{16}\) -
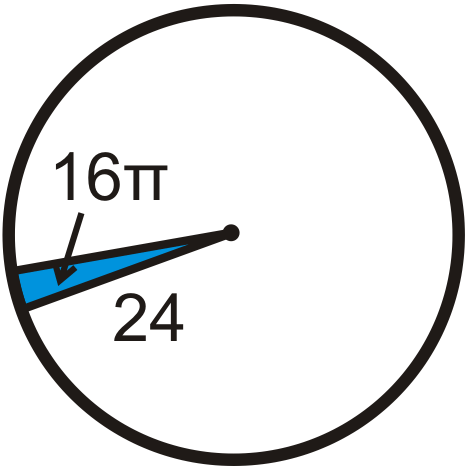
Figure \(\PageIndex{17}\) -
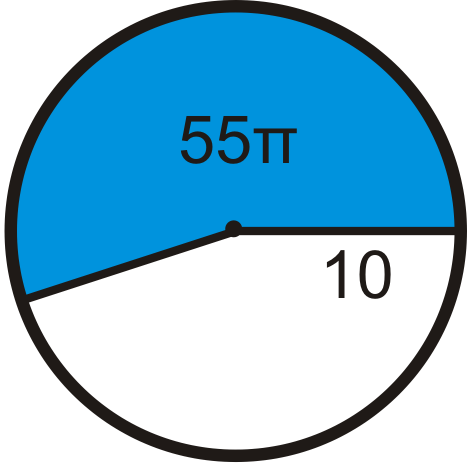
Figure \(\PageIndex{18}\)
- Find the area of the sector in ⨀A. Leave your answer in terms of \pi .
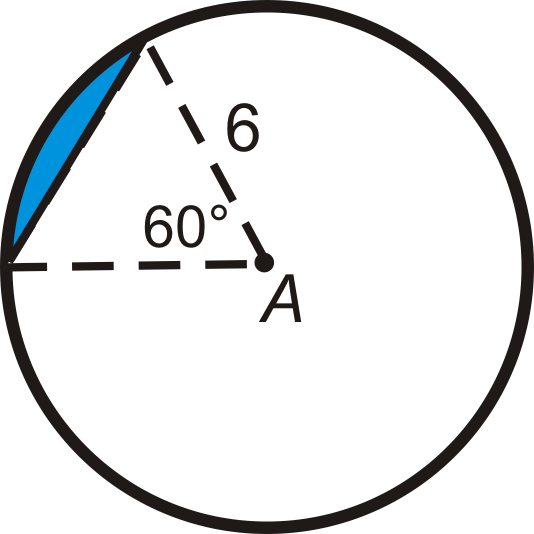
Figure \(\PageIndex{19}\) - Find the area of the equilateral triangle.
- Find the area of the segment. Round your answer to the nearest hundredth.
- Find the area of the sector in ⨀A. Leave your answer in terms of \pi .
- Find the area of the right triangle.
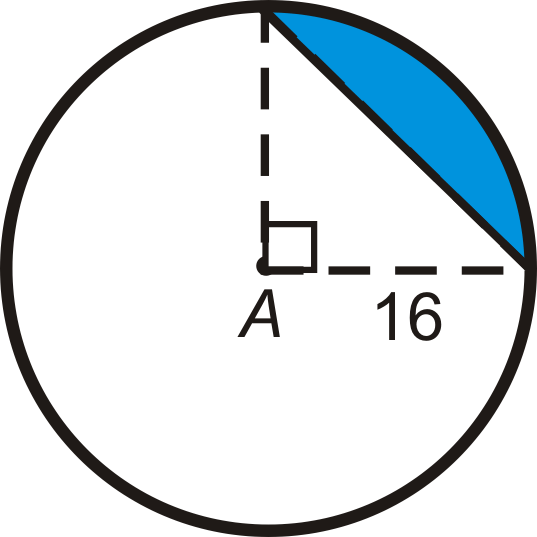
Figure \(\PageIndex{20}\) - Find the area of the segment. Round your answer to the nearest hundredth.
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.11.
Vocabulary
| Term | Definition |
|---|---|
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| pi | (or \pi ) The ratio of the circumference of a circle to its diameter. |
| radius | The distance from the center to the outer rim of a circle. |
| Arc | An arc is a section of the circumference of a circle. |
| arc length | In calculus, arc length is the length of a plane function curve over an interval. |
| radian | A radian is a unit of angle that is equal to the angle created at the center of a circle whose arc is equal in length to the radius. |
| Scale Factor | A scale factor is a ratio of the scale to the original or actual dimension written in simplest form. |
| Sector | A sector of a circle is a portion of a circle contained between two radii of the circle. Sectors can be measured in degrees. |
| Sector of a Circle | A sector of a circle is the area bounded by two radii and the arc between the endpoints of the radii. |
Additional Resources
Interactive Element
Video: Area of Sectors and Segments Principles - Basic
Activities: Area of Sectors and Segments Discussion Questions
Study Aids: Circumference and Arc Length Study Guide
Practice: Area of Sectors and Segments
Real World: Watch Out for the Weather!

