6.12: Chords and Central Angle Arcs

Arcs determined by angles whose vertex is the center of a circle and chords (segments that connect two points on a circle).

Chords in Circles

Chord Theorems

There are several important theorems about chords that will help you to analyze circles better.

1. Chord Theorem #1: In the same circle or congruent circles, minor arcs are congruent if and only if their corresponding chords are congruent.

Figure $\PageIndex{1}$

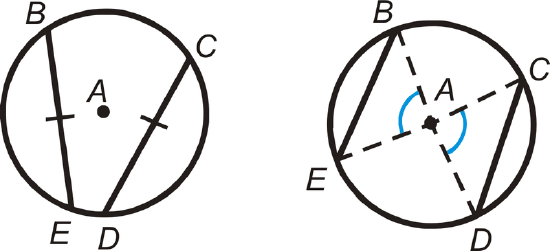
In both of these pictures, $\overline{BE}\cong \overline{CD}$ and $\widehat{BE}\cong \widehat{CD}$.

2. Chord Theorem #2: The perpendicular bisector of a chord is also a diameter.

Figure $\PageIndex{2}$

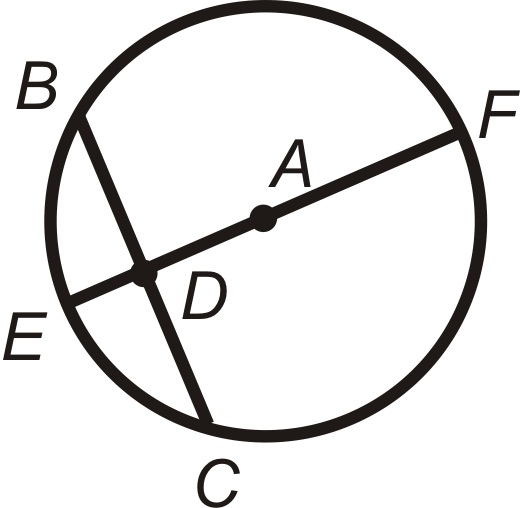
If $\overline{AD}\perp \overline{BC}$ and $\overline{BD}\cong \overline{DC}$ then $\overline{EF}$ is a diameter.

3. Chord Theorem #3: If a diameter is perpendicular to a chord, then the diameter bisects the chord and its corresponding arc.

Figure $\PageIndex{3}$

If $\overline{EF}\perp \overline{BC}$, then $\overline{BD}\cong \overline{DC}$

4. Chord Theorem #4: In the same circle or congruent circles, two chords are congruent if and only if they are equidistant from the center.

Figure $\PageIndex{4}$

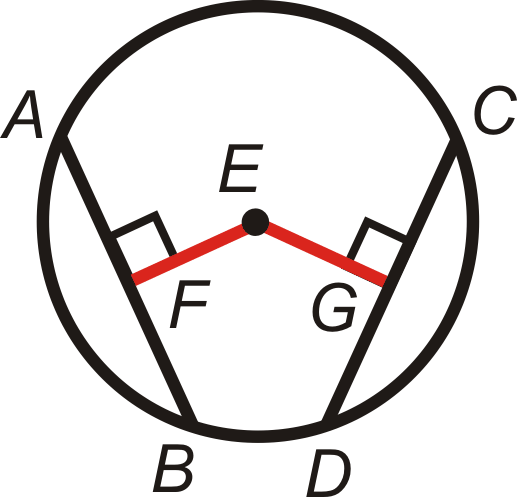
The shortest distance from any point to a line is the perpendicular line between them. If $FE=EG$ and $\overline{EF}\perp \overline{EG}$, then $\overline{AB}$ and $\overline{CD}$ are equidistant to the center and$\overline{AB}\cong \overline{CD}$.

What if you were given a circle with two chords drawn through it? How could you determine if these two chords were congruent?

Example $\PageIndex{1}$

Find the value of $x$ and $y$.

Figure $\PageIndex{5}$

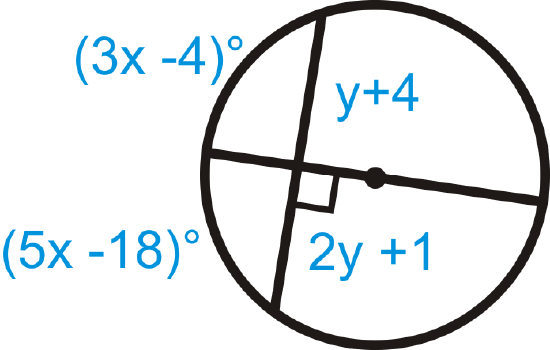
Solution

The diameter is perpendicular to the chord, which means it bisects the chord and the arc. Set up equations for $x$ and $y$.

$\begin{array}{rlr} (3 x-4)^{\circ} & =(5 x-18)^{\circ} & y+4=2 y+1 \\ 14 & =2 x & 3=y \\ 7 & =x \end{array}$

Example $\PageIndex{2}$

$BD=12$ and $AC=3$ in $\bigodot A$. Find the radius.

Figure $\PageIndex{6}$

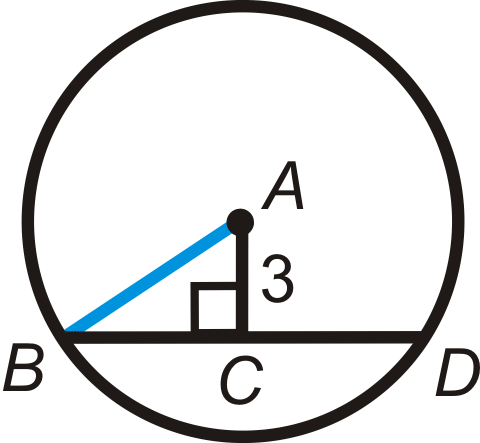
Solution

First find the radius. $\overline{AB}$ is a radius, so we can use the right triangle \Delta ABC\) with hypotenuse $\overline{AB}$. From Chord Theorem #3, $BC=6$.

$\begin{aligned} 3^2+6^2&=AB^2 \\ 9+36&=AB^2 \\ AB&=\sqrt{45}=3\sqrt{5}\end{aligned}$

Example $\PageIndex{3}$

Use $\bigodot A$ to answer the following.

Figure $\PageIndex{7}$

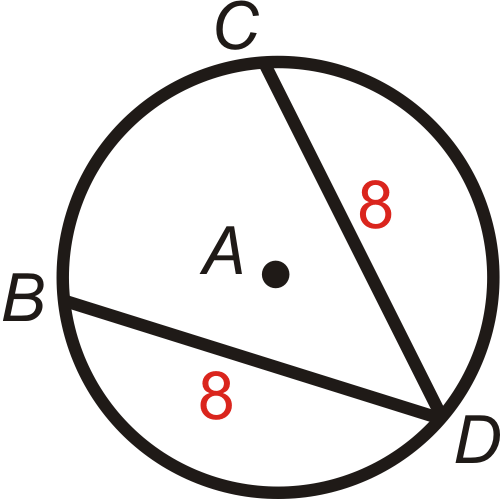
1. If $m\widehat{BD}=125^{\circ}$, find $m\widehat{CD}$.
2. If $m\widehat{BC}=80^{\circ}$, find $m\widehat{CD}$.

Solution

1. $BD=CD$, which means the arcs are congruent too. $m\widehat{CD}=125^{\circ}$.
2. $m\widehat{CD}\cong m\widehat{BD}$ because $BD=CD$.

$\begin{aligned} m\widehat{BC}+m\widehat{CD}+m\widehat{BD}&=360^{\circ} \\ 80^{\circ}+2m\widehat{CD}&=360^{\circ} \\ 2m\widehat{CD}&=280^{\circ} \\ m\widehat{CD}=140^{\circ}\end{aligned}$

Example $\PageIndex{4}$

Find the values of $x$ and $y$.

Figure $\PageIndex{8}$

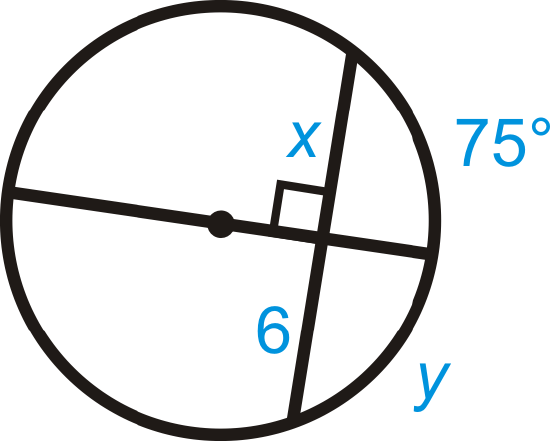
Solution

The diameter is perpendicular to the chord. From Chord Theorem #3, $x=6$ and $y=75^{\circ}$.

Example $\PageIndex{5}$

Find the value of $x$.

Figure $\PageIndex{9}$

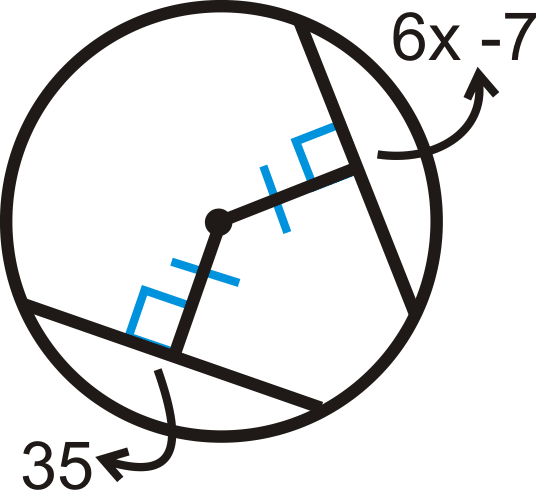
Solution

Because the distance from the center to the chords is equal, the chords are congruent.

$\begin{aligned} 6x−7&=35 \\ 6x&=42 \\ x&=7 \end{aligned}$

Review

Fill in the blanks.

Figure $\PageIndex{10}$

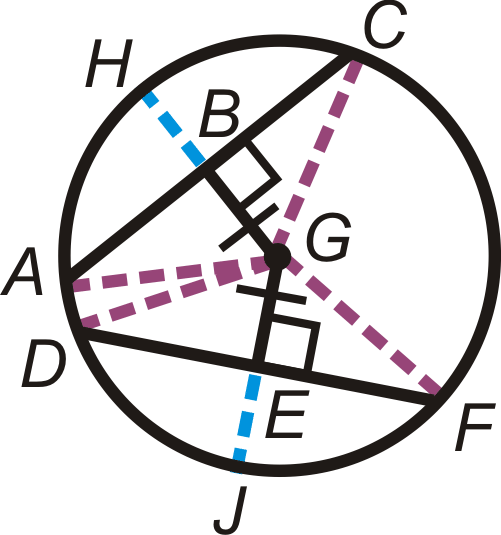
1. $\text{_____}\cong \overline{DF}$
2. $\widehat{AC} \cong \text{_____}$
3. $\widehat{DJ}\cong \text{_____}$
4. $\text{_____}\cong \overline{EJ}$
5. $\angle AGH\cong \text{_____}$
6. $\angle DGF\cong \text{_____}$
7. List all the congruent radii in $\bigodot G$.

Find the value of the indicated arc in $\bigodot A$.

8. $m\widehat{BC}$

   

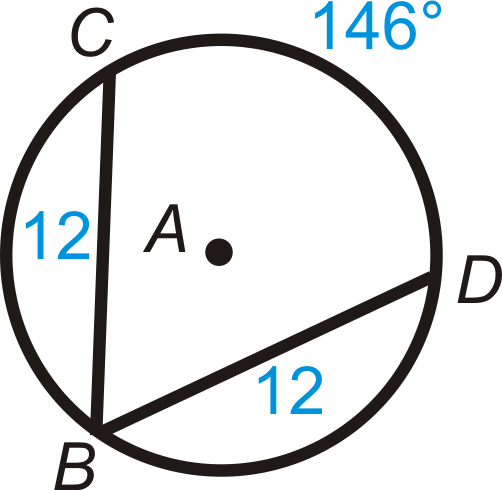
   Figure $\PageIndex{11}$

9. $m\widehat{BD}$

   

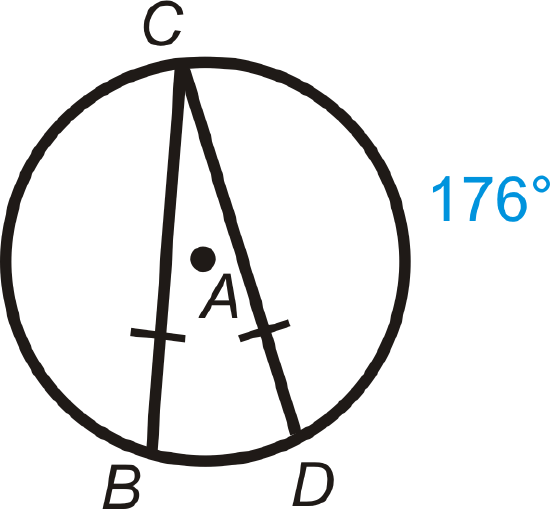
   Figure $\PageIndex{12}$

10. $m\widehat{BC}$

    

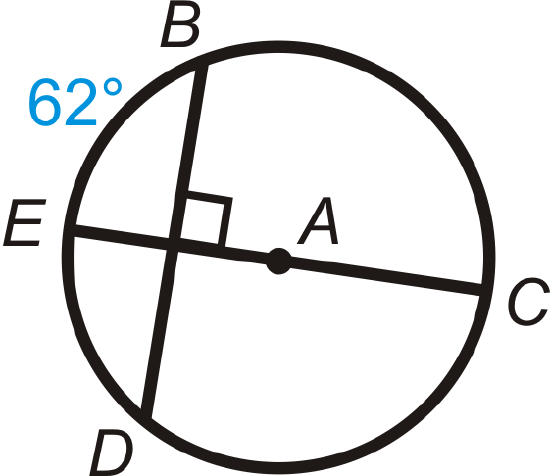
    Figure $\PageIndex{13}$

11. $m\widehat{BD}$

    

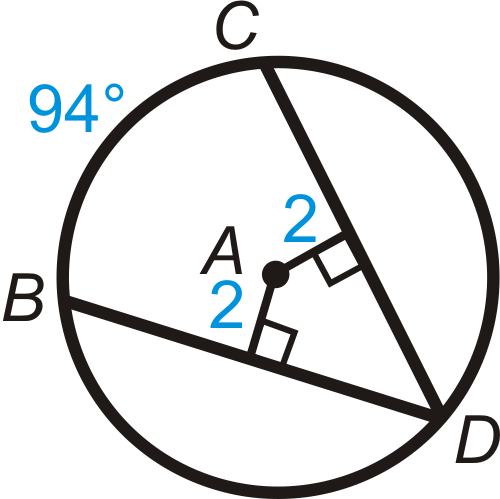
    Figure $\PageIndex{14}$

12. $m\widehat{BD}$

    

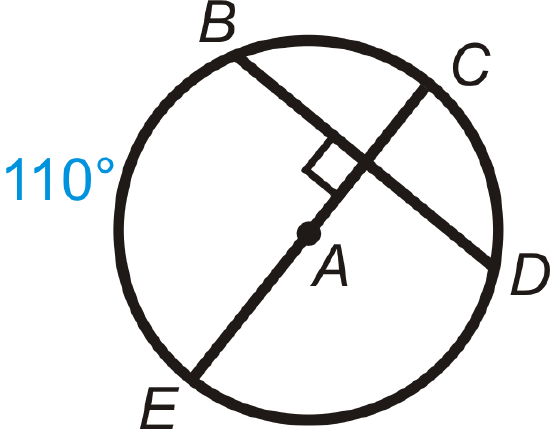
    Figure $\PageIndex{15}$

13. $m\widehat{BD}$

    

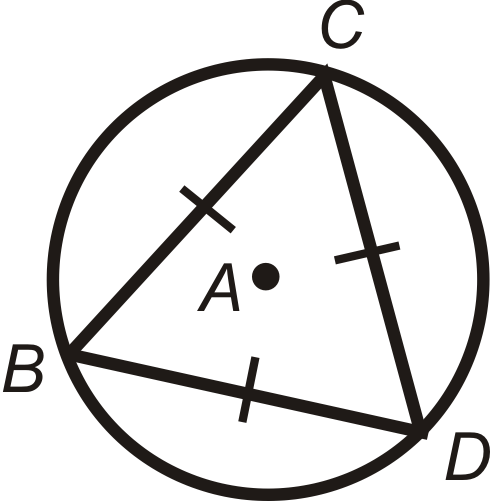
    Figure $\PageIndex{16}$

Find the value of $x$ and/or $y$.

14. 

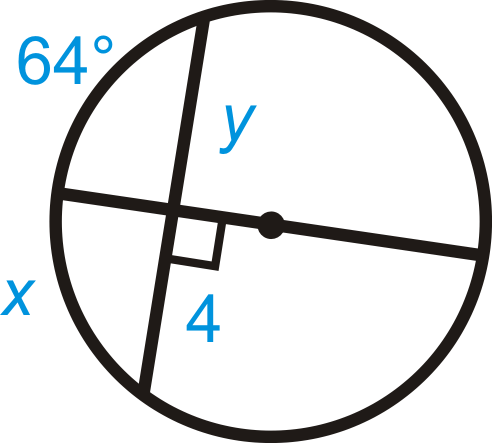
    Figure $\PageIndex{17}$

15. 

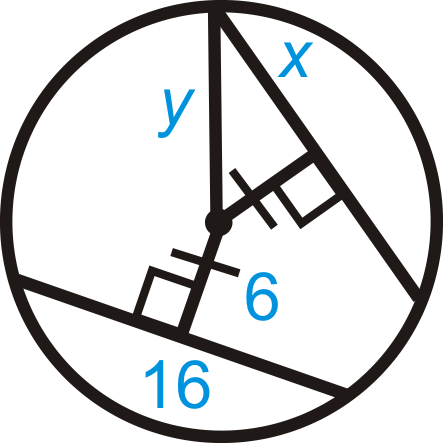
    Figure $\PageIndex{18}$

16. 

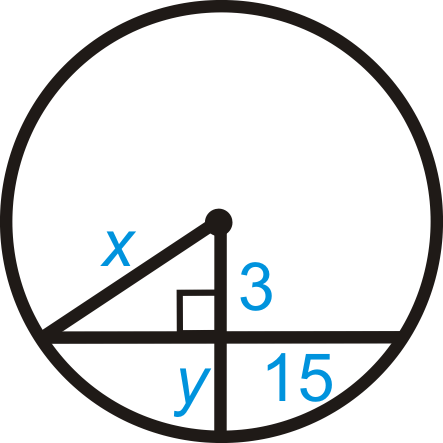
    Figure $\PageIndex{19}$

17. $AB=32$

    

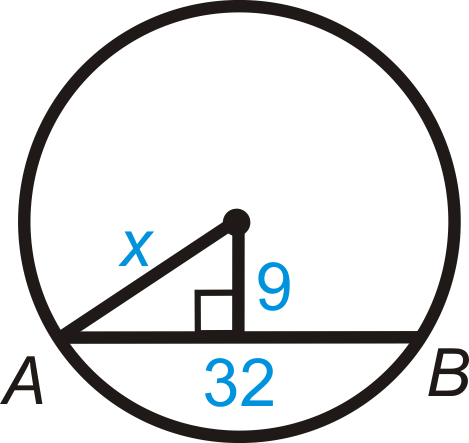
    Figure $\PageIndex{20}$

18. 

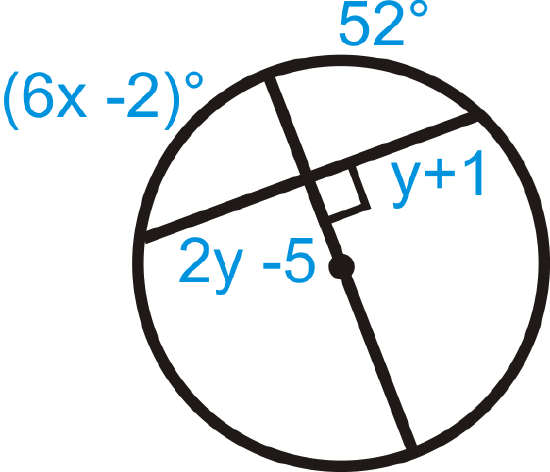
    Figure $\PageIndex{21}$

19. 

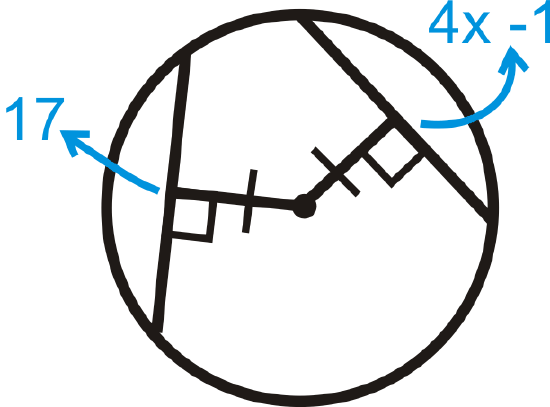
    Figure $\PageIndex{22}$

20. 

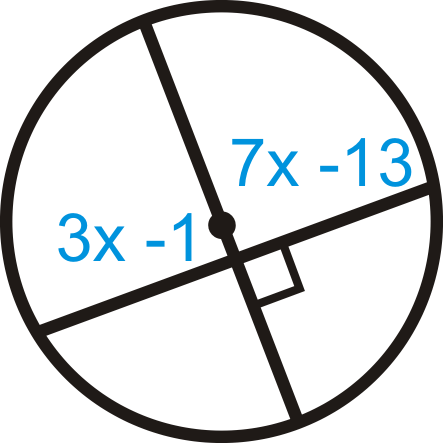
    Figure $\PageIndex{23}$

21. 

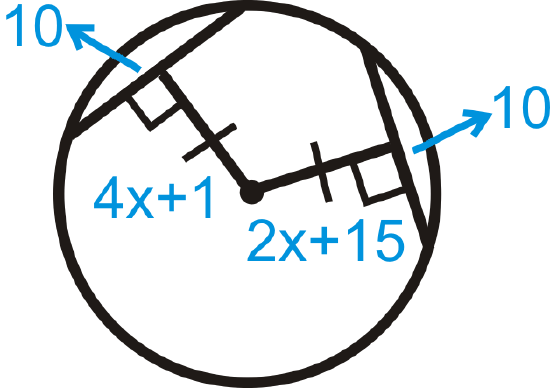
    Figure $\PageIndex{24}$

22. $AB=20$

    

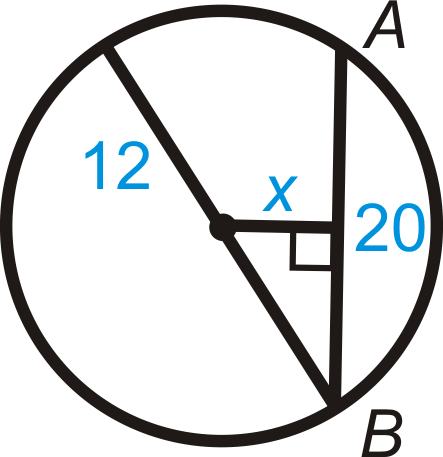
    Figure $\PageIndex{25}$

23. Find $m\widehat{AB}$ in Question 17. Round your answer to the nearest tenth of a degree.
24. Find $m\widehat{AB}$ in Question 22. Round your answer to the nearest tenth of a degree.

In problems 25-27, what can you conclude about the picture? State a theorem that justifies your answer. You may assume that A is the center of the circle.

25. 

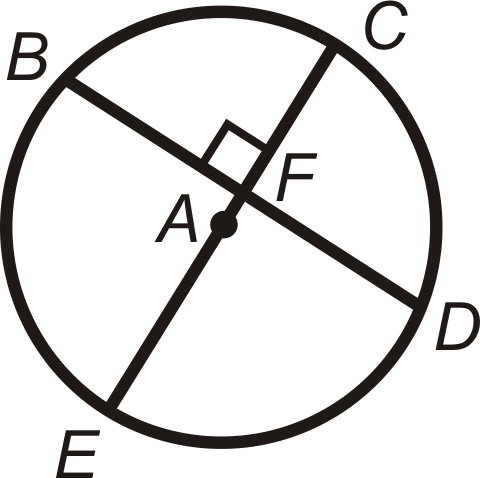
    Figure $\PageIndex{26}$

26. 

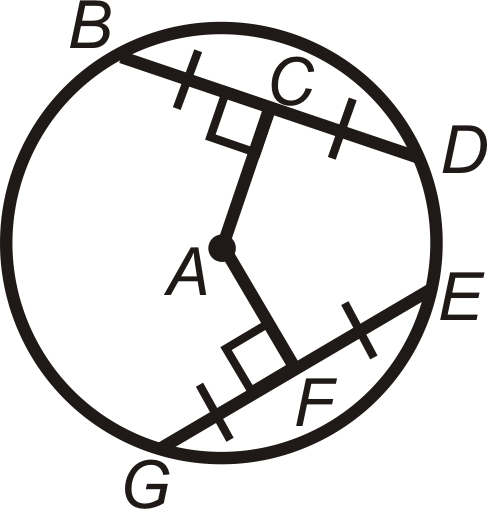
    Figure $\PageIndex{27}$

27. 

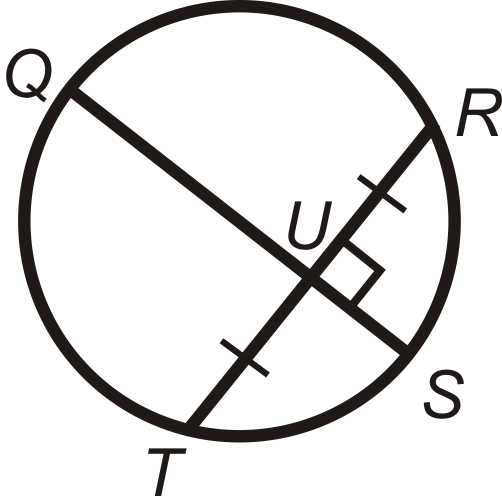
    Figure $\PageIndex{28}$

Review (Answers)

To see the Review answers, open this PDF file and look for section 9.4.

Vocabulary

Term	Definition
chord	A line segment whose endpoints are on a circle.
circle	The set of all points that are the same distance away from a specific point, called the center.
diameter	A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius.
radius	The distance from the center to the outer rim of a circle.

Additional Resources

Interactive Element

Video: Chords in Circles Principles - Basic

Activities: Chords in Circles Discussion Questions

Study Aids: Circles: Segments and Lengths Study Guide

Practice: Chords and Central Angle Arcs