6.13: Segments from Chords
- Page ID
- 5028
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Apply the Intersecting Chords Theorem.
When we have two chords that intersect inside a circle, as shown below, the two triangles that result are similar.
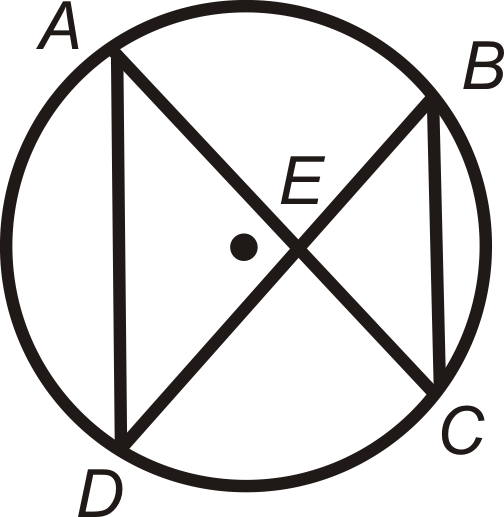
This makes the corresponding sides in each triangle proportional and leads to a relationship between the segments of the chords, as stated in the Intersecting Chords Theorem.
Intersecting Chords Theorem: If two chords intersect inside a circle so that one is divided into segments of length a and b and the other into segments of length \(c\) and \(d\) then \(ab=cd\).
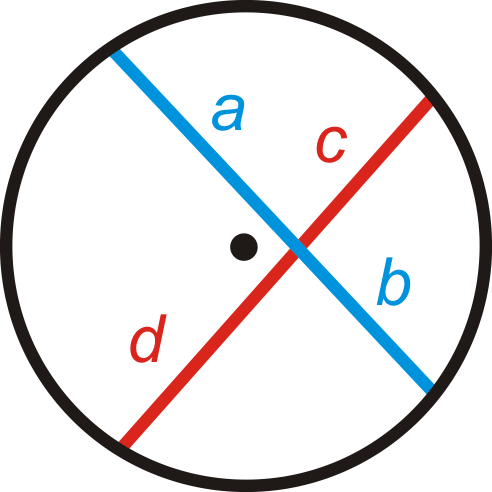
What if you were given a circle with two chords that intersect each other? How could you use the length of some of the segments formed by their intersection to determine the lengths of the unknown segments?
Example \(\PageIndex{1}\)
Find \(x\). Simplify any radicals.
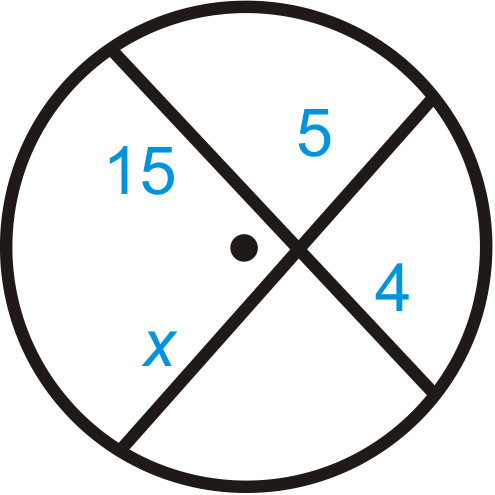
Solution
Use the Intersecting Chords Theorem.
\(15\cdot 4=5\cdot x\)
\(60=5x\)
\(x=12\)
Example \(\PageIndex{2}\)
Find \(x\). Simplify any radicals.
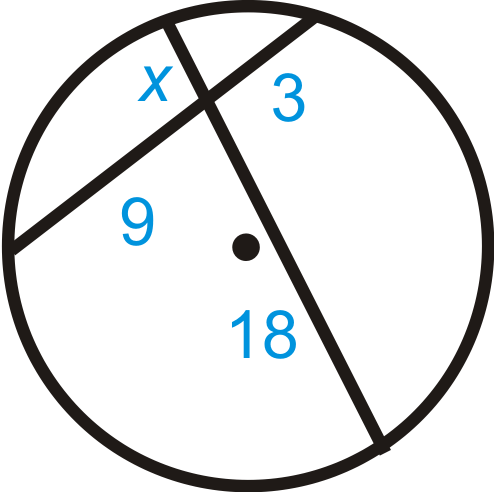
Solution
Use the Intersecting Chords Theorem.
\(\begin{aligned} 18\cdot x&=9\cdot 3 \\ 18x&=27 \\ x&=1.5\end{aligned}\)
Example \(\PageIndex{3}\)
Find x in each diagram below.
-
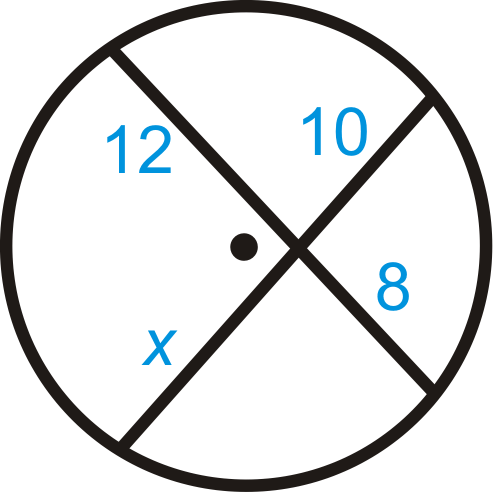
Figure \(\PageIndex{5}\) -
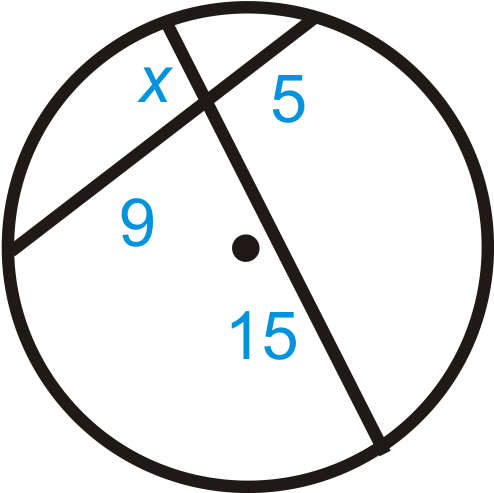
Figure \(\PageIndex{6}\
Solution
- Use the formula from the Intersecting Chords Theorem.
\(\begin{aligned}12\cdot 8 &=10\cdot x \\ 96&=10x \\ 9.6&=x\end{aligned}\)
- Use the formula from the Intersecting Chords Theorem.
\(\begin{aligned} x\cdot 15&=5\cdot 9 \\ 15x&=45 \\ x&=3 \end{aligned}\)
Example \(\PageIndex{4}\)
Solve for \(x\) in each diagram below.
-
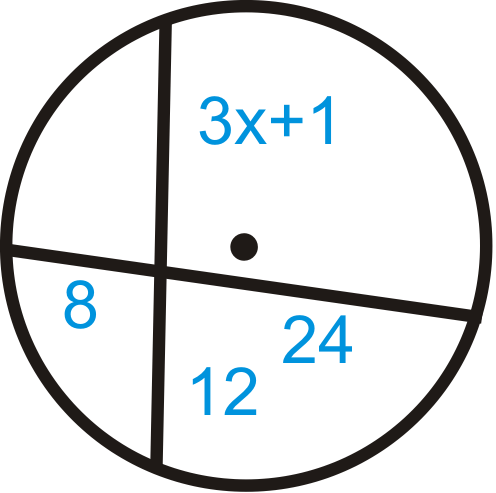
Figure \(\PageIndex{7}\) -
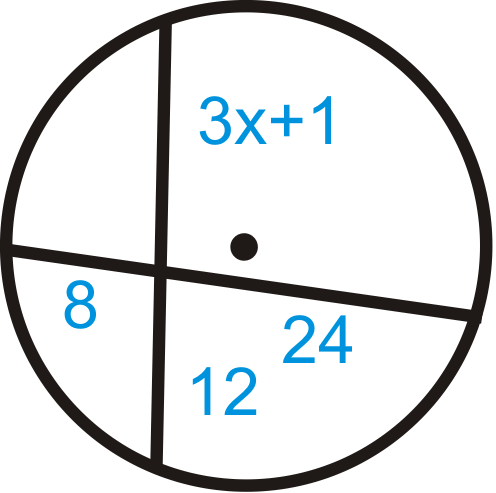
Figure \(\PageIndex{8}\)
Solution
- Use the Intersecting Chords Theorem.
\(\begin{aligned} 8\cdot 24&=(3x+1)\cdot 12 \\192&=36x+12 \\ 180&=36x \\ 5&=x\end{aligned}\)
- Use the Intersecting Chords Theorem.
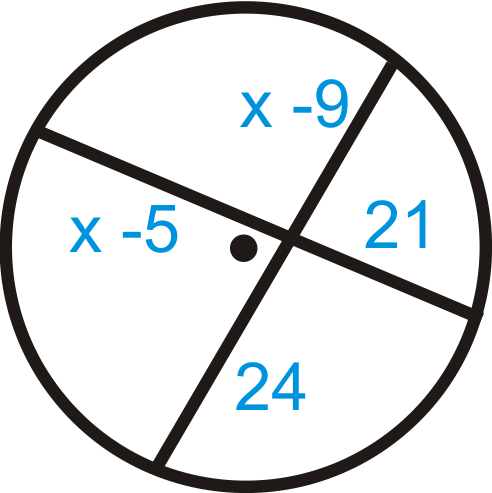
\(\begin{aligned} (x−5)21&=(x−9)24 \\ 21x−105&=24x \\ 111&=3x \\ 37−216&=x \end{aligned}\)
Example \(\PageIndex{5}\)
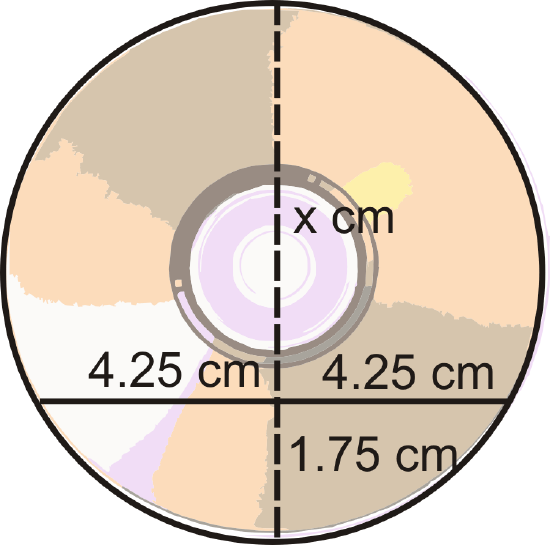
Ishmael found a broken piece of a CD in his car. He places a ruler across two points on the rim, and the length of the chord is 9.5 cm. The distance from the midpoint of this chord to the nearest point on the rim is 1.75 cm. Find the diameter of the CD.
Solution
Think of this as two chords intersecting each other. If we were to extend the 1.75 cm segment, it would be a diameter. So, if we find x in the diagram below and add it to 1.75 cm, we would find the diameter.
\(\begin{aligned} 4.25\cdot 4.25&=1.75\cdot x \\ 18.0625&=1.75x\end{aligned}\)
\(x\approx 10.3 cm, making the diameter 10.3+1.75\approx 12 cm, which\: is\: the actual diameter of a CD.\)
Review
Fill in the blanks for each problem below and then solve for the missing segment.
-
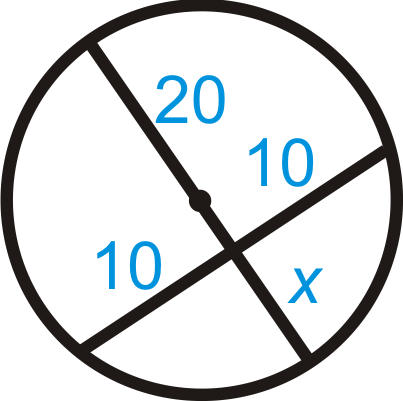
Figure \(\PageIndex{11}\)
\(20x=_______\)
-
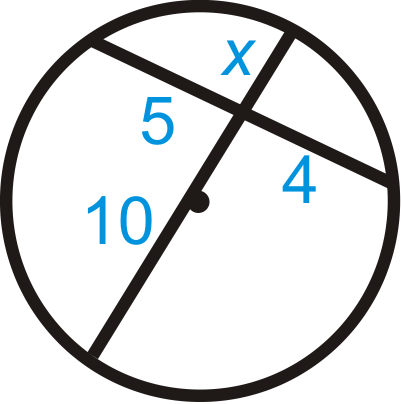
Figure \(\PageIndex{12}\)
\(\text{_______}\cdot 4=\text{_______}\cdot x\)
Find x in each diagram below. Simplify any radicals.
-
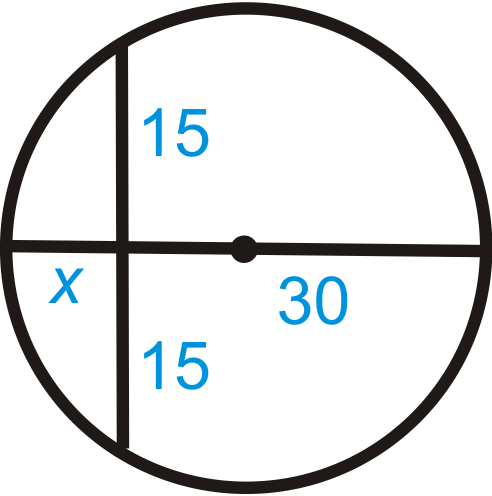
Figure \(\PageIndex{13}\) -
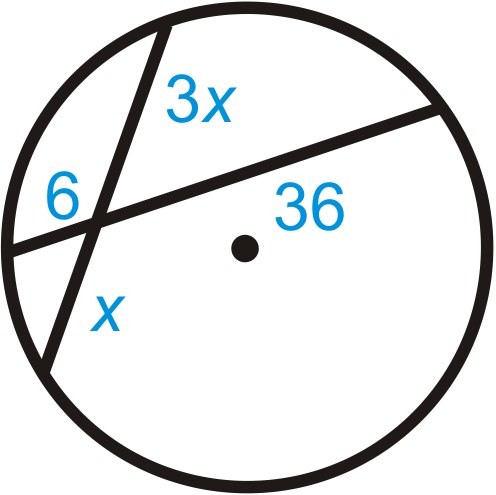
Figure \(\PageIndex{14}\) -
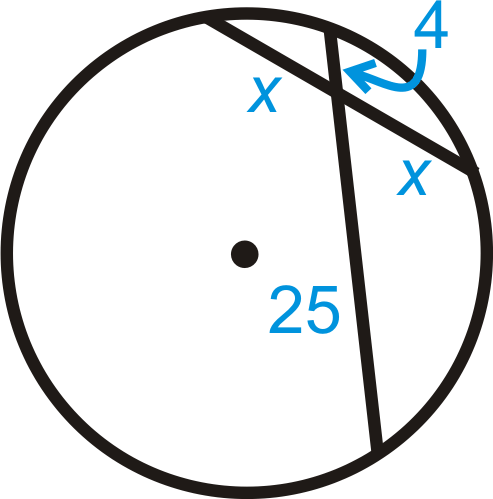
Figure \(\PageIndex{15}\)
Find the value of \(x\).
-
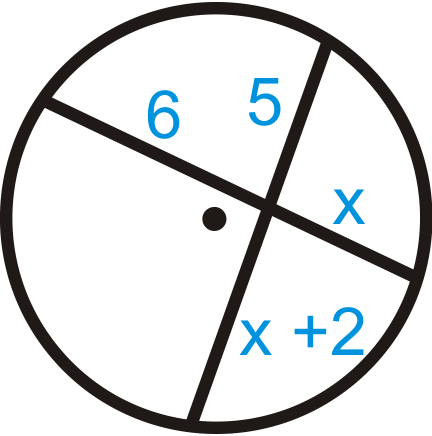Figure \(\PageIndex{16}\) -
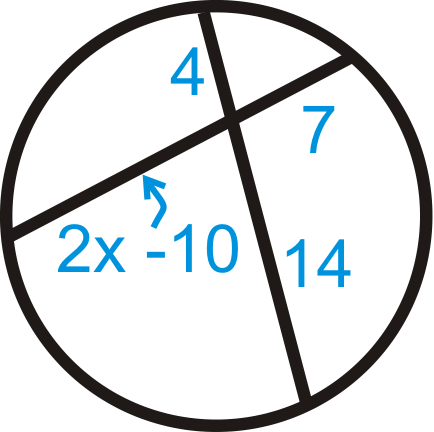
Figure \(\PageIndex{17}\) -
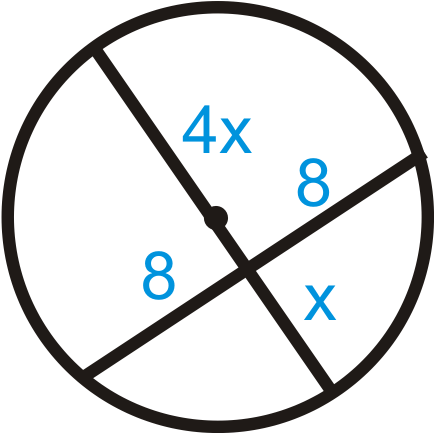
Figure \(\PageIndex{18}\) - Suzie found a piece of a broken plate. She places a ruler across two points on the rim, and the length of the chord is 6 inches. The distance from the midpoint of this chord to the nearest point on the rim is 1 inch. Find the diameter of the plate.
- Fill in the blanks of the proof of the Intersecting Chords Theorem.
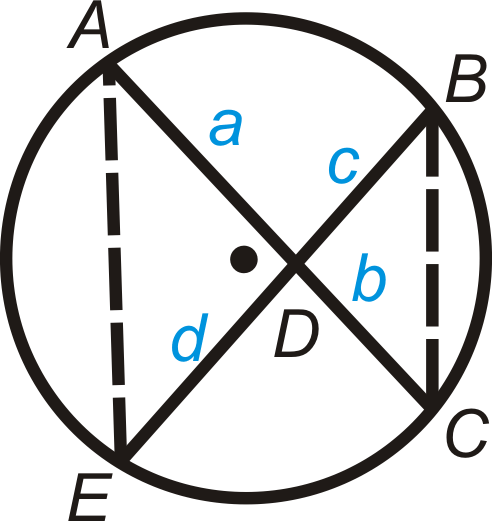
Figure \(\PageIndex{19}\)
Given: Intersecting chords \(\overline{AC}\) and \(\overline{BE}\).
Prove: \(ab=cd\)
| Statement | Reason |
|---|---|
| 1. Intersecting chords \(\overline{AC}\) and \(\overline{BE}\) with segments \(a\), \(b\), \(c\), and \(d\). | 1. |
| 2. | 2. Congruent Inscribed Angles Theorem |
| 3. \(\Delta ADE\sim \Delta BDC\) | 3. |
| 4. | 4. Corresponding parts of similar triangles are proportional |
| 5. \(ab=cd\) | 5. |
Vocabulary
| Term | Definition |
|---|---|
| central angle | An angle formed by two radii and whose vertex is at the center of the circle. |
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| inscribed angle | An angle with its vertex on the circle and whose sides are chords. |
| intercepted arc | The arc that is inside an inscribed angle and whose endpoints are on the angle. |
| radius | The distance from the center to the outer rim of a circle. |
| Intersecting Chords Theorem | According to the Intersecting Chords Theorem, if two chords intersect inside a circle so that one is divided into segments of length \(a\) and \(b\) and the other into segments of length \(c\) and \(d\), then \(ab = cd\). |
Additional Resources
Interactive Element
Video: Segments from Chords Principles - Basic
Activities: Segments from Chords Discussion Questions
Study Aids: Circles: Segments and Lengths Study Guide
Practice: Segments from Chords