6.14: Inscribed Angles in Circles
- Page ID
- 5030
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Vertex on a circle and chords as sides, and whose measure equals half the intercepted arc.
An inscribed angle is an angle with its vertex on the circle and whose sides are chords. The intercepted arc is the arc that is inside the inscribed angle and whose endpoints are on the angle. The vertex of an inscribed angle can be anywhere on the circle as long as its sides intersect the circle to form an intercepted arc.
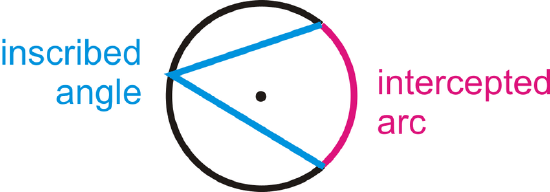
The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc.
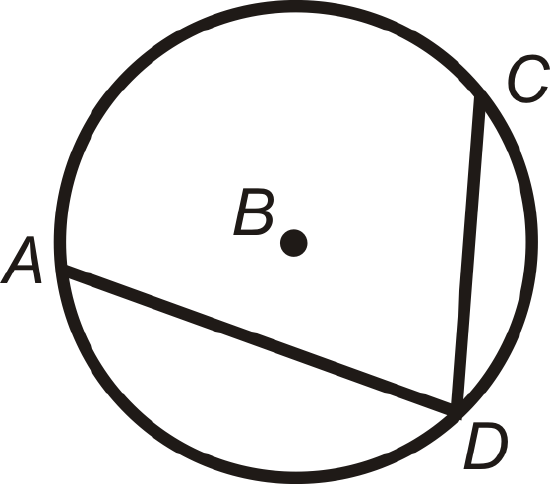
\(m\angle ADC=\dfrac{1}{2}m\widehat{AC}\) and \(m\widehat{AC}=2m\angle ADC\)
Inscribed angles that intercept the same arc are congruent. This is called the Congruent Inscribed Angles Theorem and is shown below.
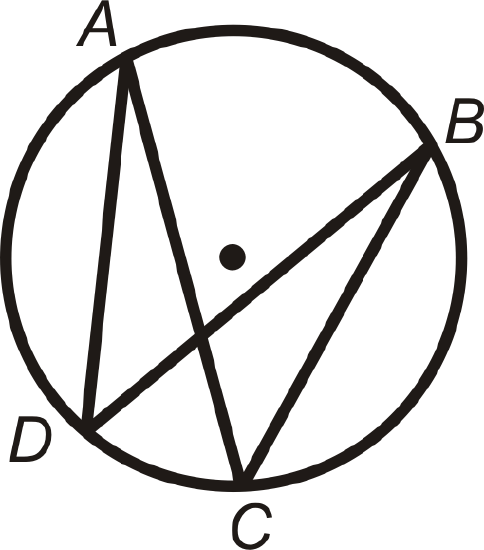
\(\angle ADB\) and \(\angle ACB\) intercept \(\widehat{AB}\), so \(m\angle ADB=m\angle ACB\). Similarly, \(\angle DAC\) and \(\angle DBC\) intercept \(\widehat{DC}\), so \(m\angle DAC=m\angle DBC\).
An angle intercepts a semicircle if and only if it is a right angle (Semicircle Theorem). Anytime a right angle is inscribed in a circle, the endpoints of the angle are the endpoints of a diameter and the diameter is the hypotenuse.
What if you had a circle with two chords that share a common endpoint? How could you use the arc formed by those chords to determine the measure of the angle those chords make inside the circle?
Example \(\PageIndex{1}\)
Find \(m\widehat{DC}\) and \(m\angle ADB\).
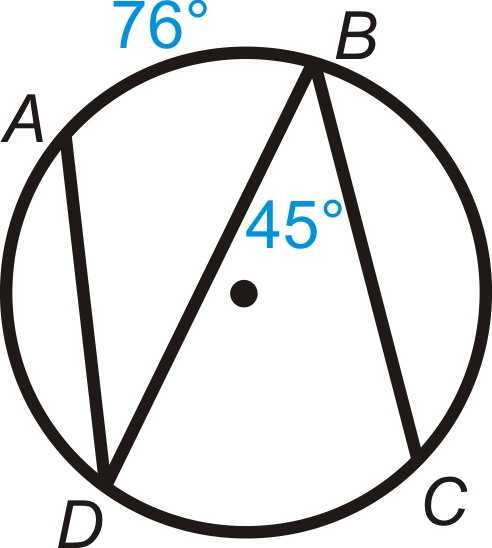
Solution
From the Inscribed Angle Theorem:
\(\begin{aligned} m\widehat{DC}&=2\cdot 45^{\circ}=90^{\circ} \\ m\angle ADB&=12\cdot 76^{\circ}=38^{\circ}\end{aligned}\)
Example \(\PageIndex{2}\)
Find \(m\angle ADB\) and \(m\angle ACB\).
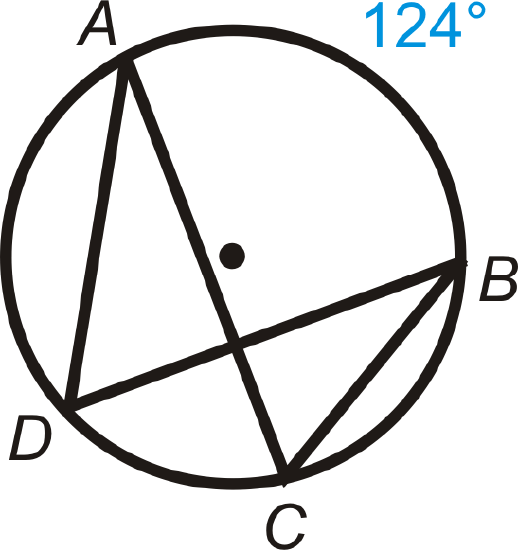
Solution
The intercepted arc for both angles is \(\widehat{AB}\). Therefore,
\(\begin{aligned} m\angle ADB&=12\cdot 124^{\circ}=62^{\circ} \\ m\angle ACB&=12\cdot 124^{\circ}=62^{\circ}\end{aligned}\)
Example \(\PageIndex{3}\)
Find \(m\angle DAB\) in \(\bigodot C\).
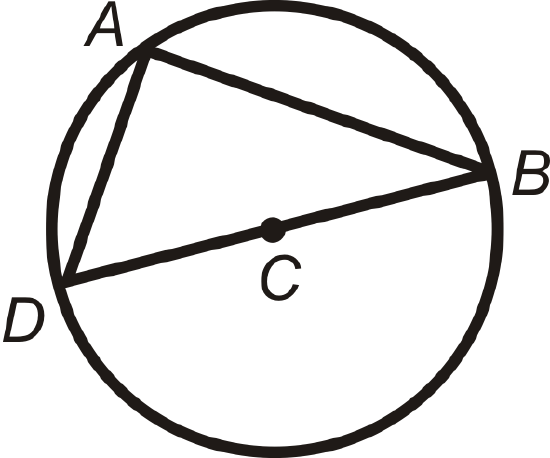
Solution
C is the center, so \(\overline{DB}\) is a diameter. \(\angle DAB\)'s endpoints are on the diameter, so the central angle is \(180^{\circ}\).
\(m\angle DAB=\dfrac{1}{2}\cdot 180^{\circ}=90^{\circ}\).
Example \(\PageIndex{4}\)
Fill in the blank: An inscribed angle is ____________ the measure of the intercepted arc.
Solution
half
Example \(\PageIndex{5}\)
Fill in the blank: A central angle is ________________ the measure of the intercepted arc.
Solution
equal to
Review
Fill in the blanks.
- An angle inscribed in a ________________ is \(90^{\circ}\).
- Two inscribed angles that intercept the same arc are _______________.
- The sides of an inscribed angle are ___________________.
- Draw inscribed angle \(\angle JKL\) in \(\bigodot M\). Then draw central angle \(\angle JML\). How do the two angles relate?
Find the value of \(x\) and/or \(y\) in \(\bigodot A\).
-
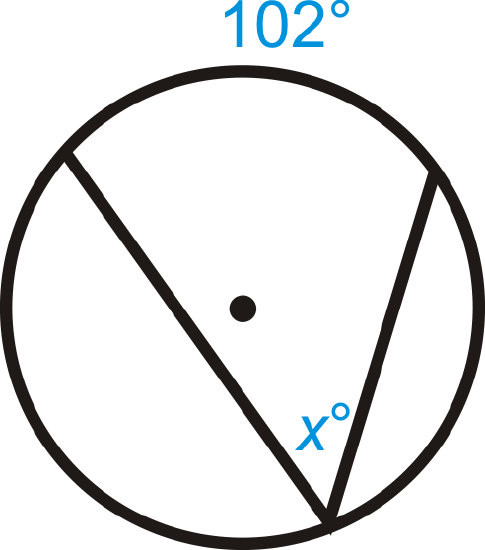Figure \(\PageIndex{7}\) -
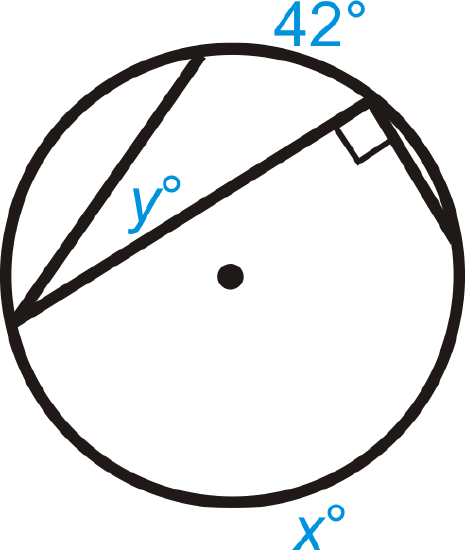Figure \(\PageIndex{8}\) -
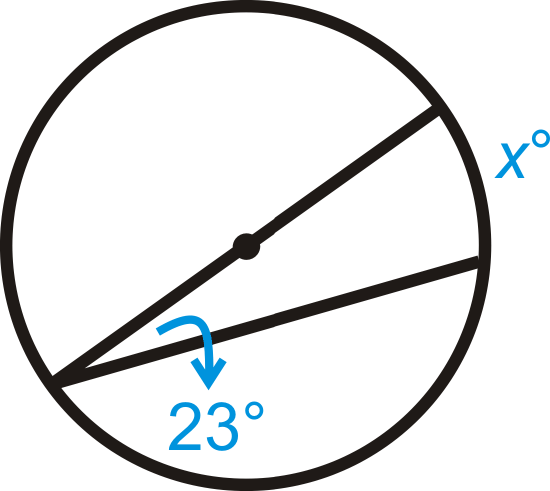Figure \(\PageIndex{9}\) -
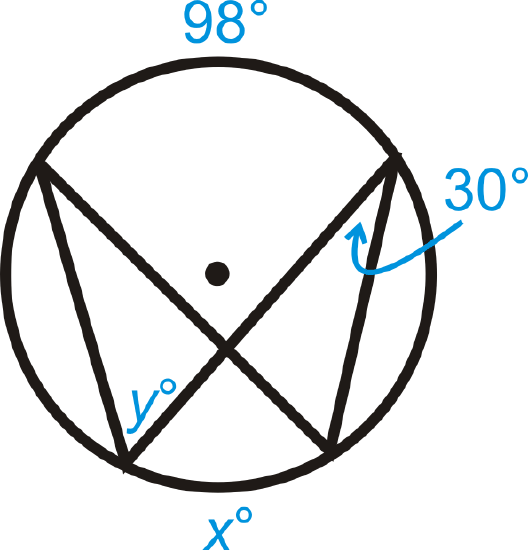Figure \(\PageIndex{10}\) -
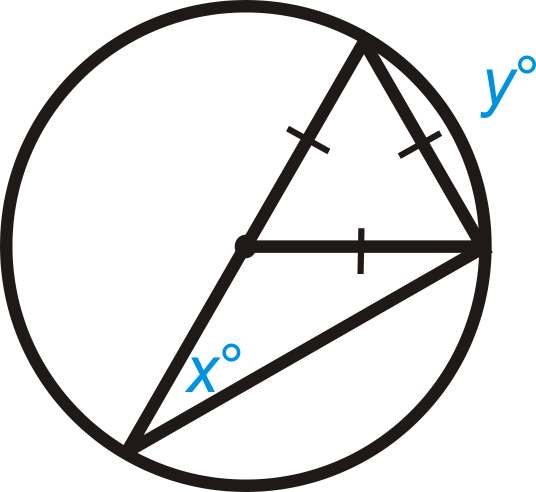Figure \(\PageIndex{11}\)
Solve for \(x\).
-
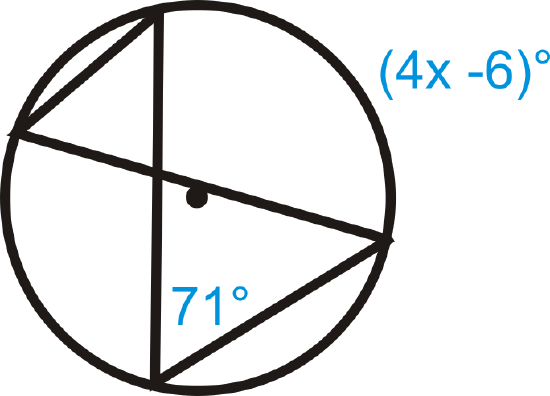Figure \(\PageIndex{12}\) -
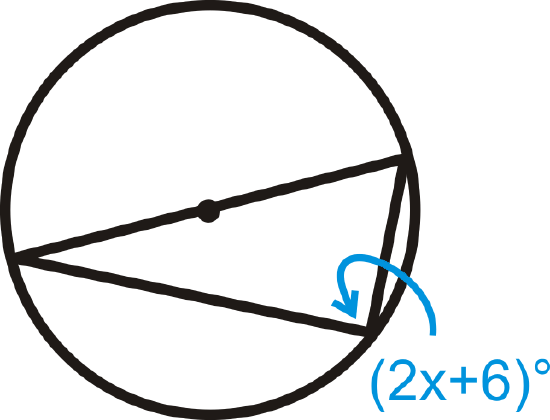Figure \(\PageIndex{13}\) -
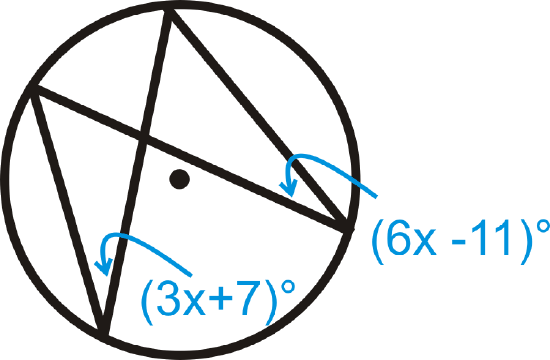Figure \(\PageIndex{14}\) -
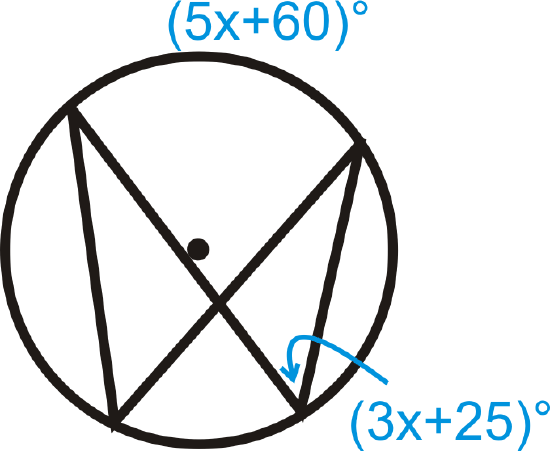Figure \(\PageIndex{15}\) - Fill in the blanks of the Inscribed Angle Theorem proof.
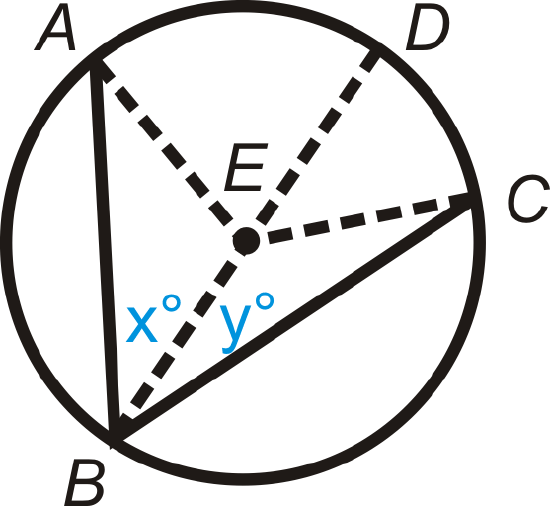Figure \(\PageIndex{16}\)
Given: Inscribed \(\angle ABC\) and diameter \(\overline{BD}\)
Prove: \(m\angle ABC=12m\widehat{AC}
| Statement | Reason |
|---|---|
|
1. Inscribed \(\angle ABC\) and diameter \(\overline{BD}\) \(m\angle ABE=x^{\circ}\) and \(m\angle CBE=y^{\circ}\) |
1. |
| 2. \(x^{\circ}+y^{\circ}=m\angle ABC\) | 2. |
| 3. | 3. All radii are congruent |
| 4. | 4. Definition of an isosceles triangle |
| 5. \(m\angle EAB=x^{\circ}\) and \(m\angle ECB=y^{\circ}\) | 5. |
| 6. \(m\angle AED=2x^{\circ}\) and \(m\angle CED=2y^{\circ}\) | 6. |
| 7. \(m\widehat{AD}=2x^{\circ}\) and \(m\widehat{DC}=2y^{\circ}\) | 7. |
| 8. | 8. Arc Addition Postulate |
| 9. \(m\widehat{AC}=2x^{\circ}+2y^{\circ}\) | 9. |
| 10. | 10. Distributive PoE |
| 11. \(m\widehat{AC}=2m\angle ABC\) | 11. |
| 12. \(m\angle ABC=\dfrac{1}{2}m\widehat{AC}\) | 12. |
Vocabulary
| Term | Definition |
|---|---|
| central angle | An angle formed by two radii and whose vertex is at the center of the circle. |
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| Inscribed Angle | An inscribed angle is an angle with its vertex on the circle. The measure of an inscribed angle is half the measure of its intercepted arc. |
| intercepted arc | The arc that is inside an inscribed angle and whose endpoints are on the angle. |
| radius | The distance from the center to the outer rim of a circle. |
| Arc | An arc is a section of the circumference of a circle. |
| Intercepts | The intercepts of a curve are the locations where the curve intersects the x and y axes. An x intercept is a point at which the curve intersects the x-axis. A y intercept is a point at which the curve intersects the y-axis. |
| Inscribed Angle Theorem | The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. |
| Semicircle Theorem | The Semicircle Theorem states that any time a right angle is inscribed in a circle, the endpoints of the angle are the endpoints of a diameter and the diameter is the hypotenuse. |
Additional Resources
Interactive Element
Video: Inscribed Angles in Circles Principles - Basic
Activities: Inscribed Angles in Circles Discussion Questions
Study Aids: Inscribed in Circles Study Guide
Practice: Inscribed Angles in Circles