3.1.4: Pythagorean Identities
- Page ID
- 4173
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sine squared plus cosine squared equals one.
he Pythagorean Theorem works on right triangles. If you consider the x coordinate of a point along the unit circle to be the cosine and the y coordinate of the point to be the sine and the distance to the origin to be 1 then the Pythagorean Theorem immediately yields the identity:
\(\begin{aligned} y^2+x^2&=1 \\ \sin ^2 x+\cos ^2 x&=1\end{aligned}\)
An observant student may guess that other Pythagorean identities exist with the rest of the trigonometric functions. Is \(\tan ^2 x+\cot ^2 x=1\) a legitimate identity?
The proof of the Pythagorean identity for sine and cosine is essentially just drawing a right triangle in a unit circle, identifying the cosine as the x coordinate, the sine as the y coordinate and 1 as the hypotenuse.
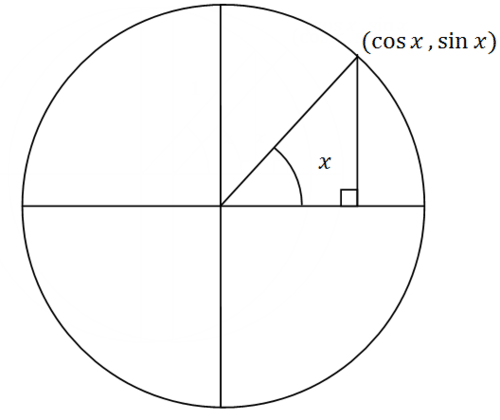
\(\cos ^2 x+\sin ^2 x=1\)
or
\(\sin ^2 x+\cos ^2 x=1\)
The two other Pythagorean identities are:
- \(1+\cot ^2 x=\csc ^2 x\)
- \(\tan ^2 x+1=\sec ^2 x\)
To derive these two Pythagorean identities, divide the original Pythagorean identity by \(\sin ^2 x\) and \(\cos ^2 x\) respectively.
To derive the Pythagorean identity \(1+\cot ^2 x=\csc ^2 x\) divide through by \(\sin ^2 x\) and simplify.
\(\begin{aligned} \dfrac{\sin ^2 x}{\sin ^2 x}+\dfrac{\cos ^2 x}{\sin ^2 x}&=\dfrac{1}{\sin ^2 x}\\ 1+\cot ^2 x&=\csc ^2 x \end{aligned}\)
Similarly, to derive the Pythagorean identity \(\tan ^2 x+1=\sec ^2 x\), divide through by \(\cos ^2 x\) and simplify.
\(\begin{aligned}\dfrac{\sin ^2 x}{\cos ^2 x}+\dfrac{\cos ^2 x}{\cos ^2 x} &=\dfrac{1}{\cos ^2 x}\\ \tan ^2 x+1 &=\sec ^2 x \end{aligned}\)
Earlier, you were asked if \(\tan ^2 x+\cot ^2 x=1\) is a legitimate identity. Cofunctions are not always connected directly through a Pythagorean identity.
\(\tan ^2 x+\cot ^2 x \neq 1\)
Solution
Visually, the right triangle connecting tangent and secant can also be observed in the unit circle. Most people do not know that tangent is named “tangent” because it refers to the distance of the line tangent from the point on the unit circle to the \(x\) axis. Look at the picture below and think about why it makes sense that \(\tan x\) and \(\sec x\) are as marked. \(\tan x=\dfrac{opp}{adj}\). Since the adjacent side is equal to 1 (the radius of the circle), \(\tan x\) simply equals the opposite side. Similar logic can explain the placement of \(\sec x\).
Simplify the following expression: \(\dfrac{\sin x(\csc x−\sin x)}{1−\sin x}\).
Solution
\(\begin{aligned}
\dfrac{\sin x(\csc x-\sin x)}{1-\sin x} &=\dfrac{\sin x \cdot \csc x-\sin ^{2} x}{1-\sin x} \\
&=\dfrac{1-\sin ^{2} x}{1-\sin x} \\
&=\dfrac{(1-\sin x)(1+\sin x)}{1-\sin x} \\
&=1+\sin x
\end{aligned}\)
Note that factoring the Pythagorean identity is one of the most powerful and common applications.
Prove the following trigonometric identity: \((\sec ^2 x+\csc ^2 x)−(\tan ^2 x+\cot ^2 x)=2\)
Solution
Group the terms and apply a different form of the second two Pythagorean identities which are \(1+\cot ^2 x=\csc ^2 x\) and \(\tan ^2 x+1=\sec ^2 x\).
\(\begin{aligned} (\sec ^2 x+\csc ^2 x)−(\tan ^2 x+\cot ^2 x) &=\sec ^2 x−\tan ^2 x+\csc ^2 x−\cot ^2 x \\&=1+1\\&=2\end{aligned}\)
Simplify the following expression. Note: \(\sec ^2 x=\dfrac{1}{\cos ^2 x}\)
Solution
\((\sec ^2 x)(1−\sin ^2 x)−(\dfrac{\sin x}{\csc x}+\dfrac{\cos x}{\sec x})\)
\(\begin{aligned} (\sec ^2 x)(1−\sin ^2 x)−(\dfrac{\sin x}{\csc x}+\dfrac{\cos x}{\sec x})&=\sec ^2 x\cdot \cos ^2 x−(\sin ^2 x+\cos ^2 x) \\ &=1−1 \\&=0\end{aligned}\)
Simplify the following expression.
\((\cos t−\sin t)^2+(cost+\sin t)^2\)
Solution
Note that initially, the expression is not the same as the Pythagorean identity.
\(\begin{aligned} (\cos t−\sin t)^2+(\cos t+\sin t)^2&=\cos^2t−2\cos t \sin t+sin^2t+cos^2t+2 \cos t \sin t+\sin^2 t\\&=1−2\cos t \sin t+1+2\cos t \sin t \\&=2\end{aligned}\)
Review
- Prove each of the following:
- \((1−\cos ^2 x)(1+\cot ^2 x)=1\)
- \(\cos x(1−\sin ^2 x)=cos^3 x\)
- \(\sin ^2 x=(1−\cos x)(1+\cos x)\)
- \(\sin x=\dfrac{\sin ^2 x+\cos ^2 x}{\csc x}\)
- \(sin^4x−cos^4x=\sin ^2 x−\cos ^2 x\)
- \(\sin ^2 x cos ^3x=(\sin ^2 x− \sin^4x)(\cos x)\)
Simplify each expression as much as possible.
- \(\tan^3x \csc^3x\)
- \(\dfrac{\csc^2x−1}{sec^2x}\)
- \(\dfrac{1−\sin ^2 x}{1+\sin x}\)
- \(\sqrt{1−\cos ^2 x}\)
- \(\dfrac{\sin ^2 x−sin^4 x}{\cos ^2 x}\)
- \((1+\tan ^2 x)(\sec ^2 x)\)
- \(\dfrac{\sin ^2 x+\tan ^2 x+\cos ^2 x}{\sec x}\)
- \(\dfrac{1+\tan ^2 x}{\csc ^2 x}\)
- \(\dfrac{1−\sin ^2 x}{\cos x}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.2.
Vocabulary
| Term | Definition |
|---|---|
| identity | An identity is a mathematical sentence involving the symbol “=” that is always true for variables within the domains of the expressions on either side. |
| Pythagorean Identity | The Pythagorean identity is a relationship showing that the sine of an angle squared plus the cosine of an angle squared is equal to one. |
| Pythagorean Theorem | The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by \(a^2+b^2=c^2\), where a and b are legs of the triangle and c is the hypotenuse of the triangle. |
Additional Resources
Video: The Reciprocal, Quotient, and Pythagorean Identities
Practice: Pythagorean Identities