5.3.1: Imaginary Numbers
- Page ID
- 4159
The imaginary number 'i' is equal to the square root of negative 1.
From Quadratics to Complex Numbers
This section introduces imaginary and complex numbers in the context of solutions to quadratic equations that don't have real-number solutions.
Warm-Up
The locations where quadratic functions cross the x−axis represent the solutions to the function. Use the interactive below to graph different parabolas. Later in this section you will see how complex numbers can be used to represent solutions to quadratic functions that do not cross the x−axis twice.
Add interactive element text here. This box will NOT print up in pdfs
Work it Out 1
Start with the quadratic equation: \(y=x^2−9\).
- Use the interactive below to graph the equation.
- Recall that the solutions to an equation are the x-values that make \(y=0\). Estimate the location(s) on the graph that represent these \((x,y)\) points. Round to the nearest whole number.
- Substitute the \(x\)-coordinates in place of \(x\) in the original equation, \(y=x^2−9\). Explain how to use the result to determine if your estimates were accurate.
Add interactive element text here. This box will NOT print up in pdfs
Discussion
What are the \(y\)-coordinates of any point on the x-axis? What are the \(x\)-coordinates of the locations where the graph crosses the \(x\)-axis?
Recall that the solutions to a quadratic equation are the values for \(x\) that make \(y\) equal to zero. If you check your answers by substituting them back into the equation, do they make \(y=0\)?
Work it Out 2
Start with the quadratic equation: \(y=2x^2−2x+2\).
- Use the interactive to graph the equation.
- Recall that the solutions to an equation are the \(x\)-values that make \(y=0\). Estimate the location on the graph that represents these \((x,y)\) points. Explain any difficulties you encounter.
Discussion
Why were you not able to visualize where along the curve there is an \(x\)-value that makes \(y=0\)?
Since the graph isn't helpful, how else might you find the solution(s) to the equation: \(0=2x^2−2x+2\)?
Work it Out 3: The Quadratic Formula and the Discriminant
Using the interactive from Active Learning 1, consider the graphs of each of these quadratic equations. They are given in the form: \(y=ax^2+bx+c\). Pay particular attention to the number of places the graph intersects the x-axis in each equation.
- \(y=0.5x^2−x−4\)
- \(y=x^2−2x+1\)
- \(y=x^2+2x+4\)
Remember, the Quadratic Formula is: \(x= \dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\). The binomial term below the radical sign, \(b^2−4ac\), is called the discriminant.
Calculate the discriminant for each of the three equations that you graphed.
Next, compare the value of the discriminant and the graph of each quadratic equation, paying particular attention to whether the discriminant is less than, equal to, or greater than zero. What do you notice? Based on your findings, how many solutions do you think there are for a quadratic equation where the discriminant is greater than, less than, or equal to zero?
Discussion
The graph below is of the first equation: \(y=\dfrac{1}{2} x^2−x−4\).
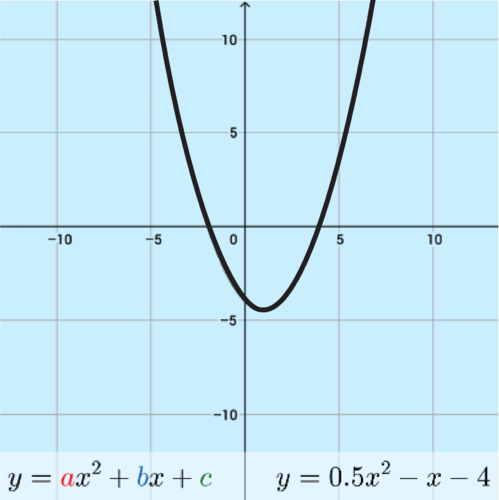
You can calculate the discriminant from this equation as follows:
\(\begin{aligned} \text{Given: }a&=\dfrac{1}{2}, b=-1, c=-4 \\ &=(-1)^2−4\left(\dfrac{1}{2}\right)(-4) \\ &=1−(-8) \\ &=9 \end{aligned}\)
When the discriminant of a quadratic equation is positive, the equation will have two, distinct, real number solutions. In this case, the solutions are \(x=-2\) and \(x=4\).
Determine the discriminant of the other two equations. What generalization can you make relating the number of real solutions to the value of the discriminant being positive, negative, or zero?
The Discriminant and Solutions to Quadratic Equations
Calculate the discriminant of the equation \(y=2x^2−5x+4\), and use that information to make a statement about the solutions.
Solution
The discriminant can be calculated as follows:
\(\begin{aligned} \text{Given: } b&=-5, a=2, c=4 \\ &=b^2−4(a)(c) \\ &=(-5)^2−4(2)(4) \\ &=-7\end{aligned}\)
Because the discriminant is less than zero, this equation has no real solutions.
Consider the equation \(y=2x^2−5x+4\) from this example. Because the discriminant is less than 0, this equation has no real solutions. However, it does have two non-real solutions. In other words, the solutions to this quadratic equation include an imaginary component. Numbers with a real component and an imaginary component are called complex.
Imaginary and Complex Numbers
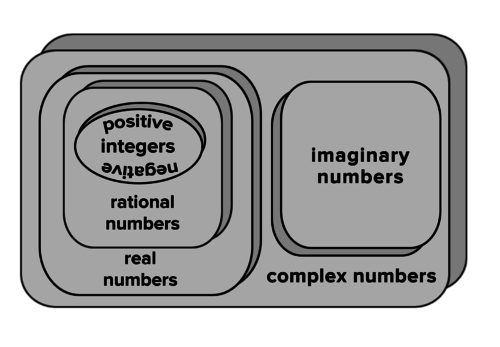
When humans first created the concept of numbers, they only had the counting numbers (whole numbers greater than zero) 1, 2, 3... and so on, because numbers were intended to count physical objects. For a long time, it was accepted that the square root of a negative number did not exist.
In order for a solution to exist to the equation x2=-1, mathematicians invented a solution. This solution is called the imaginary number and is noted by the letter i. The imaginary numbers, 1i,2i,3i... are called imaginary because they cannot be found on a traditional number line of real numbers.
A pure imaginary number is a number in the form bi where b is a nonzero real number. Examples include \(4i\), \(i\sqrt{2}\), and \(−6i\).
A complex number has both real and imaginary parts, and is written in the form a\pm bi. Interestingly, any number can be written as a complex number, since either the real or imaginary component can either be zero or have a zero coefficient.
Examples of Complex Numbers
- The set of Complex Numbers is a 'superset' of all other number sets. That means every other set of numbers is part of the Complex Number set.
- Complex numbers appear in the form \(a+bi\), where \(a\) and \(b\) are Real Numbers, and \(i=\sqrt{-1}\).
- ANY number may be written as a Complex Number:
\(\begin{aligned} \text{The Real Number 4 in Complex form} && =4+0i\\ \text{The Imaginary Number } 5i \text{ in Complex form} && =0+5i\\ \text{The Complex Number } 4+5i \text{ in Complex form } && =4+5i \end{aligned}\)
Given that \(\sqrt{-1}=i\), what is \(i^2\) equivalent to? Explain why this is remarkable.
Solution
Before trying to answer this question, think about how you'd answer this question for positive numbers. For example, 9–√=3, and therefore, by squaring both sides: \(3^2=9\). Similarly, \(\sqrt{49}=7\), and therefore \(49=7^2\). So if -1−−√=i, what happens to each side of the equation if you square both sides? In other words, what is \(i^2\) equivalent to?
\(\begin{aligned} i^2&=i\cdot i \\ &=\sqrt{-1} \cdot \sqrt{-1} \\&=(\sqrt{-1})^2 \\ &=(-1) \\&=-1 \end{aligned}\)
One entertaining way to think of this is to consider how odd it would be if two imaginary people were able to have a real child together. This is similar in concept to the result of squaring an imaginary number, or multiplying two imaginary numbers together.

The square root of any negative number can be written in terms of the imaginary number i. Rewrite the following as imaginary numbers:
- \(\sqrt{-4}\)
- \(\sqrt{-5}\)
- \(\sqrt{-6}\)
Solution
- \(\sqrt{4}=\sqrt{4\cdot -1}=\sqrt{4}\sqrt{-1}=2i\)
- \(\sqrt{-5}=\sqrt{5\cdot -1}=\sqrt{5}\sqrt{-1}=i\sqrt{5}\)
- \(\sqrt{-16}=\sqrt{16\cdot -1}=\sqrt{16}\sqrt{-1}=4i\)
Work it Out 4
Simplify the following:
- \(\sqrt{-49}\)
- \(\sqrt{-40}\)
Discussion
If you can reduce the number under the radical after you've turned it into a positive number, you should do so.
\(\begin{aligned} \sqrt{-49} \\ &=\sqrt{49\cdot -1} \\ &=\sqrt{49}\sqrt{-1} \\ &=7i \end{aligned}\)
Simplify \(\sqrt{-40}\) similarly, but don't forget to simplify \(\sqrt{40}\) after you deal with the square root of -1.
Work it Out 5
The parabola \(y=x^2−2x+3\) has no \(x\)-intercepts, as shown below. Does this mean that there are no solutions? How could complex numbers help with solving the equation \(0=x^2−2x+3\)? What are the solutions to this function?
Discussion
The graph below shows that the curve of this equation doesn't intersect with the x-axis.
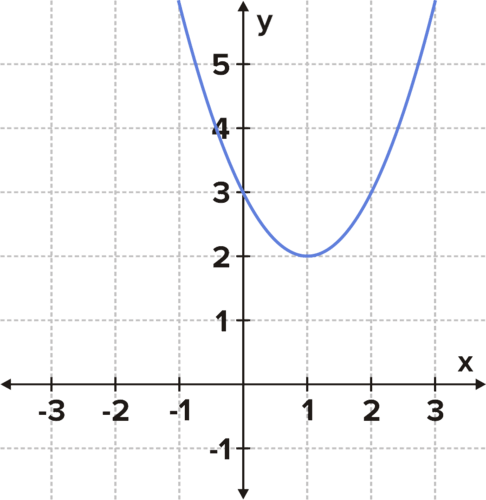
This means that the solutions to the equation \(x^2−2x+3=0\) are not real numbers. The solutions are complex numbers (which involve real and imaginary parts). The solutions can still be found using the quadratic formula, but the result will be 2 complex number solutions. What are they?
The following video demonstrates how to determine the complex solutions of a quadratic equation.
Work it Out 6: Complex Number Solutions to Quadratic Functions
Recall that when the value of the discriminant is less than zero, the equation has two unequal complex number solutions. Substitute \(-1+2i\) into the quadratic equation \(x^2+2x+5=0\) to determine if it is a solution. Use what you determine from the substitution to make an educated guess at what another solution might be. Test that solution also.
Discussion
Just as with any other quadratic equation, to check a solution, substitute the solution in place of \(x\), and simplify the expression to determine whether or not it is equal to zero.
CK-12 INTERACTIVE
The following CK-12 PLIX, "Vertical and Horizontal Shift 2," offers an additional chance to explore complex roots of quadratics.
Complex Number Solutions to Quadratic Functions
Is \(\dfrac{3}{2}−i\) a solution to \(2x^2−6x+5=0\)?
Solution
Substitute the coefficients into the quadratic formula, and simplify to generate the equation:
\(\begin{aligned}
& \dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\
=& \dfrac{6 \pm \sqrt{(-6)^{2}-4(2)(5)}}{2(2)} \\
=& \dfrac{6 \pm \sqrt{(36)-40}}{4} \\
=& \dfrac{6 \pm \sqrt{-4}}{4} \\
x=&\left\{\dfrac{3}{2}+\dfrac{1}{2} i\right\} \text { or }\left\{\dfrac{3}{2}-\dfrac{1}{2} i\right\}
\end{aligned}\)
When simplified, since neither of the solutions is the one stated in the problem, namely \(\dfrac{3}{2}−i\), it is not a solution.
Alternatively, you could substitute in the given solution and see if the equation equals zero.
\(\begin{array}{r}
2\left(\dfrac{3}{2}-i\right)^{2}-6\left(\dfrac{3}{2}-i\right)+5=0 ? \\
2\left(\dfrac{9}{4}-3 i+i^{2}\right)-6\left(\dfrac{3}{2}-i\right)+5=0 ? \\
2\left(\dfrac{9}{4}-3 i+(-1)\right)-6\left(\dfrac{3}{2}-i\right)+5=0 ? \\
2\left(\dfrac{5}{4}-3 i\right)-6\left(\dfrac{3}{2}-i\right)+5=0 ? \\
\dfrac{5}{2}-\cancel{6 i}-9+\cancel{6i}+5=0 ? \\
-\dfrac{3}{2} \neq 0
\end{array}\)
Since it doesn't equal zero, \(\dfrac{3}{2}−i\) is not a solution.
Review
- Use a graphing utility like the interactive at the beginning of this lesson to graph the equation \(x^2+2x+1=0\). Use the graph to determine the solution to the equation, and then use Algebra to confirm your answer is correct.
Calculate the discriminant:
- \(6x^2+10−1=0\)
- \(3x^2+24x+48=0 \)
Create quadratics:
- Compose a quadratic function with two real solutions.
- Compose a quadratic function with one real and one imaginary solution.
- Compose a quadratic function with two imaginary solutions.
Express each as a simplified imaginary number.
- \(\sqrt{-300}\)
- \(\sqrt{-32}\)
- \(4\sqrt{-18}\)
- \(\sqrt{-75}\)
- \(\sqrt{-98}\)
Solve each equation and express the result as a complex number.
- \(8x^2−5x+11=0\)
- \(34\dfrac{1}{2}x^2−23x+19\dfrac{1}{6}=0\)

