7.6: HIV
- Page ID
- 12190
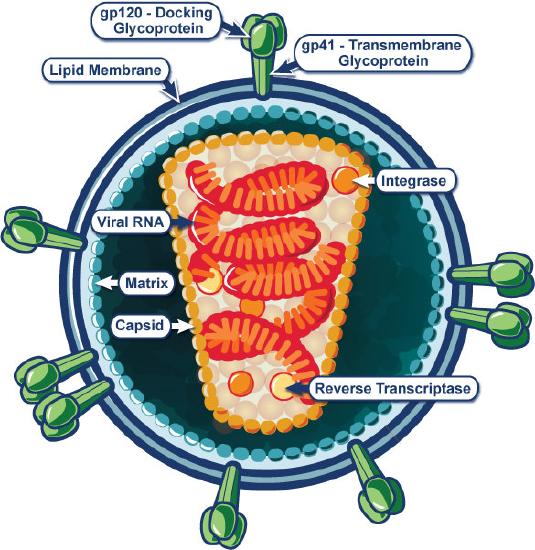
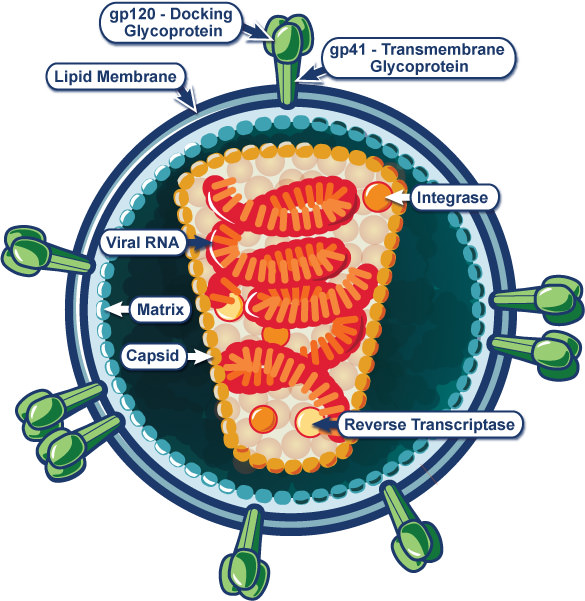
Why is the shape of the virus important?
The AIDS virus. One of the most devastating viruses known. Why? Notice the intricate anatomy of the virus, both inside and outside. It is the constant changing of those outside markers that make producing a vaccine against this virus difficult.
HIV
The Human Immunodeficiency Virus (HIV) is the virus that causes Acquired Immunodeficiency Syndrome (AIDS). Most researchers believe that the HIV originated in sub-Saharan Africa during the 20th century. HIV is transmitted by sexual contact and by contact with infected bodily fluids, such as blood, semen, breast milk, and vaginal secretions. It is also passed from mother to fetus. HIV is now a pandemic, with an estimated (as of 2008) 38.6 million people now living with the disease worldwide. It is estimated that AIDS has killed more than 25 million people since it was first recognized in 1981.
HIV is the retrovirus that destroys the immune system. HIV primarily infects helper T cells (specifically CD4+ T cells), macrophages, and dendritic cells. HIV infection leads to low levels of CD4+ T cells because the virus directly kills infected cells and the infected T cells are also attacked by the immune system. The infection of a CD4 cell is shown in the Figure below. When CD4+ T cell numbers decline below a certain critical level, cell-mediated immunity is lost, and the body becomes more prone to opportunistic infections. HIV infections will be discussed further in the immune system concepts.
If left untreated, most HIV-infected individuals will develop AIDS. AIDS is a collection of symptoms and infections resulting from the damage to the immune system by HIV. Because the immune systems of people with AIDS are so weak, bacteria and viruses that do not normally cause disease in healthy people can easily cause disease in an AIDS patient. Opportunistic infections associated with AIDS include:
- Pneumocystis pneumonia: a form of pneumonia caused by a fungus.
- Tuberculosis (TB), caused by the Mycobacterium tuberculosis bacteria.
- Lung infections caused by Mycobacterium other than tuberculosis (MOTT).
- Kaposi's sarcoma: a type of cancer that is caused by Kaposi's sarcoma-associated herpesvirus (KSHV).
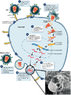
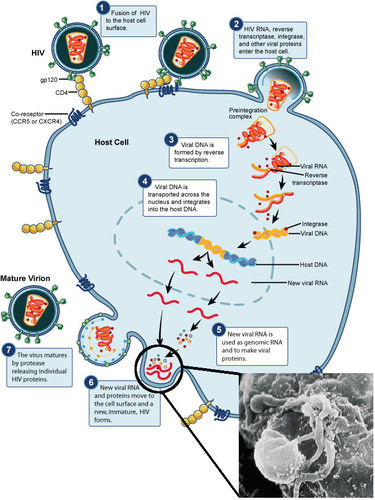 Lifecycle of HIV. The image at bottom right is an SEM of HIV budding from cultured lymphocyte. The many round bumps on the cell surface are sites of assembly and budding of virions.
Lifecycle of HIV. The image at bottom right is an SEM of HIV budding from cultured lymphocyte. The many round bumps on the cell surface are sites of assembly and budding of virions.An HIV Infection
An HIV infection of a CD4 cell can be summarized as follows:
- First, the viral particle attaches to the CD4 receptor and other associated receptors on the cell membrane. The viral envelope then fuses with the cell membrane, and the viral capsid moves into the cell.
- Once the viral capsid enters the cell, reverse transcriptase frees the single-stranded RNA from the viral proteins and copies it into a complementary strand of DNA. This process of reverse transcription is error-prone and it is during this step that mutations may occur. Such mutations may cause drug resistance.
- The reverse transcriptase then makes a complementary DNA strand to form a double-stranded viral DNA (vDNA).
- The vDNA is then moved into the cell nucleus. The integration of the viral DNA into the host cell's genome is carried out by another viral enzyme called integrase. This integrated viral DNA may then lie dormant, during the latent stage of the HIV infection. Clinical latency for HIV can vary between two weeks and 20 years.
- To actively produce viruses, certain cellular transcription factors need to be present. These transcription factors are plentiful in activated T cells. This means that those cells most likely to be killed by HIV are those currently fighting infection. The virus DNA is transcribed to mRNA which then leads to new virus protein and genome production.
- Viral particles are assembled inside the cell and then exit the cell by budding. The virus gets its viral envelope from the cell’s plasma membrane. The cycle begins again when the new particles infect another cell.
HIV infection is treated with a cocktail of several antiretroviral drugs. The antiretroviral drugs prevent the virus from replicating and destroying more T cells, thus preventing the patients from developing AIDS. Treatment with antiretroviral drugs can dramatically increase the life expectancy of people with HIV.
Summary
- HIV is the virus that causes AIDS. HIV destroys the immune system.
- Opportunistic infections lead to AIDS.
Review
1. Describe the relationship between HIV and AIDS.
The graph below shows the relationship between the number of HIV particles and CD4 lymphocyte counts over the course of an untreated HIV infection. Use the graph to answer the following questions:
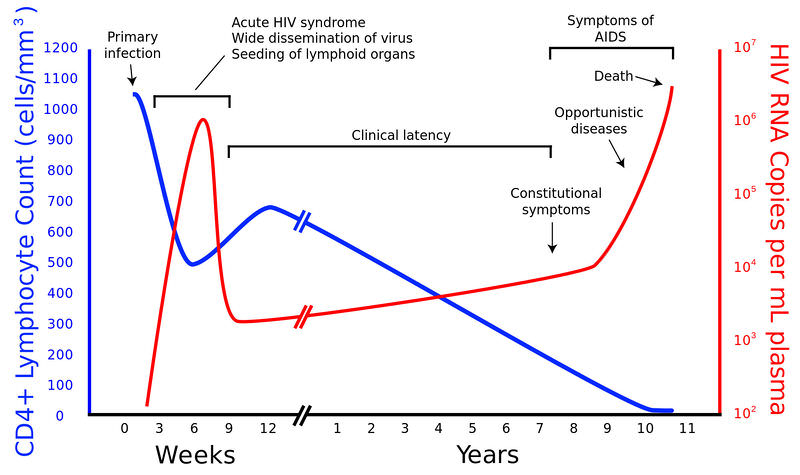
2. How does the increase of the number of HIV particles relate to the path of the disease?
3. Outline what happens to the number of viruses and numbers of lymphocytes between three and six weeks after initial infection.
4. Can the development of AIDS symptoms be delayed? Explain your answer.
| Image | Reference | Attributions |
 |
[Figure 1] | Credit: Diagram: Courtesy of the NIAID; SEM image: Courtesy of CDC/C. Goldsmith, P. Feorino, E. L. Palmer, W. R. McManus Source: Diagram: http://www.niaid.nih.gov/topics/HIVAIDS/Understanding/Biology/pages/hivreplicationcycle.aspx ; SEM image: commons.wikimedia.org/wiki/File:HIV-budding.jpg License: CC BY-NC |
 |
[Figure 2] | Credit: Diagram: Courtesy of the NIAID; SEM image: Courtesy of CDC/C. Goldsmith, P. Feorino, E. L. Palmer, W. R. McManus Source: Diagram: http://www.niaid.nih.gov/topics/HIVAIDS/Understanding/Biology/pages/hivreplicationcycle.aspx ; SEM image: commons.wikimedia.org/wiki/File:HIV-budding.jpg License: Public Domain |
 |
[Figure 3] | Credit: Diagram: Courtesy of the NIAID; SEM image: Courtesy of CDC/C. Goldsmith, P. Feorino, E. L. Palmer, W. R. McManus Source: Diagram: http://www.niaid.nih.gov/topics/HIVAIDS/Understanding/Biology/pages/hivreplicationcycle.aspx ; SEM image: commons.wikimedia.org/wiki/File:HIV-budding.jpg License: CC BY-NC |

