2.4: Location

How could you locate this feature?

Geologists, hikers, and many other people need to be able to say where they are. Or where they want to go. They need to be able to mark a location on a map. The opening photo is of Old Faithful Geyser in Yellowstone National Park. It is located at 44°30'N and 110°150'W. Let’s explore what that means.

Location

To describe your location, you could use a coordinate system. To do this you need two points. For example, you could use streets. Maybe you are at the corner of Maple Avenue and Main Street. Or you could use a point of reference, a distance and an angle for direction. If you want to meet up with a friend, you could tell him “I am two blocks due north of your apartment.” Can you identify the point of reference, the distance, and the angle?

Map Coordinates

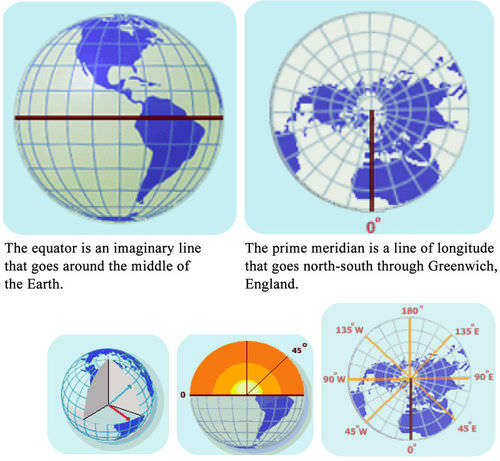
Most maps use a grid of lines to help you to find your location. This grid system is called a geographic coordinate system. Using this system you can define your location by two numbers, latitude and longitude. Both numbers are angles between your location, the center of Earth, and a reference line (Figure below).

Lines of latitude start with the Equator. Lines of longitude begin at the prime meridian.

Latitude

Lines of latitude circle around Earth. The Equator is a line of latitude right in the middle of the planet. Latitude is divided into degrees: 90° north of the Equator and 90° south of the Equator. One degree is subdivided into 60 minutes. One minute is subdivided into 60 seconds. The Equator is at 0°. The Equator is an equal distance from both the North and South Poles. If you know your latitude, you know how far you are north or south of the Equator.

Longitude

Lines of longitude are circles that go around Earth from pole to pole, like the sections of an orange. Longitude is also measured in degrees, which are subdivided into minutes and seconds. Lines of longitude start at the Prime Meridian, which is 0°. The Prime Meridian is a circle that runs north to south and passes through Greenwich, England. Longitude tells you how far you are east or west from the Prime Meridian (Figure below). On the opposite side of the planet from the Prime Meridian is the International Date Line. It is at 180°. This is the place where a new day first arrives.

Lines of latitude and longitude form convenient reference points on a map.

You can remember latitude and longitude by doing jumping jacks. When your hands are above your head and your feet are together, say longitude (your body is long!). When you put your arms out to the side horizontally, say latitude (your head and arms make a cross, like the “t” in latitude). While you are jumping, your arms are going the same way as each of these grid lines: horizontal for latitude and vertical for longitude.

Using Latitude and Longitude on a Map

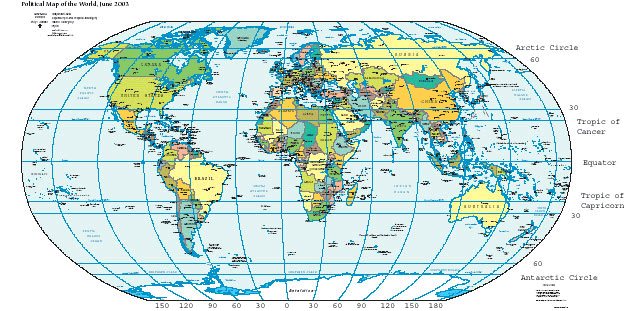
If you know the latitude and longitude of a place, you can find it on a map. Simply place one finger on the latitude on the vertical axis of the map. Place your other finger on the longitude along the horizontal axis of the map. Move your fingers along the latitude and longitude lines until they meet. For example, say the location you want to find is at 30°N and 90°W. Place your right finger along 30°N at the right of the map. Place your left finger along the bottom at 90°W. Move your fingers along the lines until they meet. Your location should be near New Orleans, Louisiana, along the Gulf coast of the United States. Now can you locate Old Faithful, 44°30'N and 110°150'W, on a map?

What if you want to know the latitude and longitude of your location? If you know where you are on a map, point to the place with your fingers. Take one finger and move it along the latitude line to find your latitude. Then move another finger along the longitude line to find your longitude.

Global Positioning System

In order to get latitude, longitude, and elevation you need several instruments. What if you could do the same thing with only one instrument? A Global Positioning System (GPS) receiver is all that is needed to locate your position on the Earth’s surface in many places.

By 1993, the United States military had launched 24 satellites to help soldiers locate their positions on battlefields. This system of satellites was called the Global Positioning System (GPS). Later, the United States government allowed the public to use this system. Here’s how it works.

(a) You need a GPS receiver to use the GPS system. (b) It takes signals from four GPS satellites to find your location precisely on the surface.

You must have a GPS receiver to use the system. You can buy many types of these in stores. The GPS receiver detects radio signals from nearby GPS satellites. There are precise clocks on each satellite and in the receiver. The receiver measures the time for radio signals from satellites to reach it. The receiver uses the time and the speed of radio signals to calculate the distance between the receiver and the satellite. The receiver does this with at least four different satellites to locate its position on the Earth’s surface (Figure above). GPS receivers are now being built into many items, such as cell phones and cars.

You can use a GPS meter to tell you how to get to Old Faithful.

Summary

• Latitude is the distance north or south of the Equator. It is expressed as a number between 0° and 90° north or south.
• Longitude is the distance east or west of the Prime Meridian. It is expressed as a number between 0° and 180° east or west.
• The global positioning system uses satellites to display very accurate location information on a special receiver.

Review

1. What would a latitude number in the Southern Hemisphere look like?
2. Define latitude and longitude.
3. Why are GPS devices so accurate?

Explore More

Use the resource below to answer the questions that follow.

1. What is latitude and what does a measurement of latitude give?
2. What is longitude and what does a measurement of longitude give?
3. By looking at the latitude image, tell where the vertex of the latitude lines is?
4. Where is the 90-degree North latitude line?
5. How many longitude lines go through the South Pole?
6. Is the United States in the Eastern or Western Hemisphere? What about India?