9.1: Keplers Laws
- Page ID
- 5669
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Much of our real scientific understanding about the solar system began when the Renaissance astronomer, Nicolaus Copernicus (1473 - 1543) promoted the novel idea that the Earth was not the center of the universe. Instead, the Earth and other planets orbited the Sun and other stars appeared as fixed points on the celestial sphere.

While many intellectuals in the mid 1500's quietly agreed with the Copernican view, Danish astronomer Tycho Brahe (1546 - 1601) was a formidable opponent. Tycho was known for his scrupulous measurements of the positions of planets in our solar system and he had an agenda: he expected to prove that the ptolomeic model was correct: the Sun orbited the Earth in a circular path and the other planets executed complicated epicyclic motions as they danced around the Earth. To his immense frustration, Tycho's belief was never supported by the data and upon his death, his assistant and eventual successor, Johannes Kepler (1571 - 1630), used Tycho's data to prove that Copernicus was correct: the planets all orbited the Sun.
The TYCHO catalog
The European Space Agency compiled the precise positions and motions of 2.5 Million stars and named the catalog in honor of Tycho Brahe.
Kepler was a religious man who believed in the intrinsic beauty and mathematical perfection of a universe created by God. Since circular orbits represented a mathematical ideal, Kepler initially assumed that planetary orbits in the solar system would be exactly circular. To his credit, he was able to reconsider this belief when the data better supported an elliptical orbit for the orbit of Mars was better described by a ellipse than a circle. Using Tycho Brahe's data, Kepler established three important laws for understanding the motion of planets in our solar system.
Kepler's Laws
- Planets move in ellipses with the Sun at the focus of the ellipse.
- Planets sweep out equal areas in equal time intervals.
- The square of the orbital period is proportional to the cube of the semi-major axis.
Kepler's First Law
Kepler's first law simply says that planetary orbits are elliptical and that the Sun is at the focus of the ellipse. In the mathematical description of an ellipse, the distance from the center of the ellipse to the widest part of the ellipse is the semi-major axis, \(a\), and the distance from the center to the narrowest side of the ellipse defines the semi-minor axis, \(b\). So at it's widest point, the ellipse has a diameter of \(2a\) and the narrowest dimension is \(2b\). A circle is a special type of ellipse with a radius such that \(a\,=\,b\).
In the figure below, the semi-major and semi-minor axes of a diagram representing an elliptical orbit are labeled. The Sun is at the focus of the ellipse and the distance between the Sun and the planet (the red dashed line) will change throughout the orbit. There are two special points in the orbit along the semi-major axes: perihelion is the point in the elliptical orbit where the planet makes its closest approach to the Sun and aphelion is the point in the orbit where the planet is farthest away.
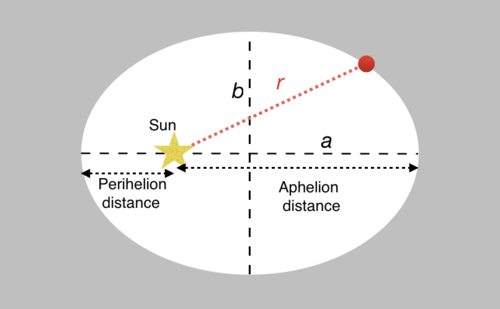
The distance between a star and planet, \(r\), is given by the following expression, where \(a\) is the semi-major axis, \(e\) is the orbital eccentricity, and \(\theta\) is the angle starting as zero at perihelion and sweeping around the orbit:
\[r\,=\frac{a(1-e^2)}{1+ecos\theta}\]
By definition, the planet will be at perihelion when \(\theta\,=\,0\) and the planet will be at aphelion when \(\theta\,=\pi\) and those distances can be calculated from the equation above:
\[r_{perihelion}\,=\,a(1-e)\]
\[r_{aphelion}\,=\,a(1+e)\]
The distance between the center of the ellipse and the focus of the ellipse is \(ae\).
Kepler's Second Law
Kepler's Second Law says that a planet will sweep out equal areas in an orbit in equal time intervals (figure below). Note that the planet does NOT sweep out equal angles in equal time intervals unless the orbit is a circle. In the Figure below, the triangular area defined by the star and points 1 and 2 has an area equal to the area defined by the star and points 3 and 4.
Kepler's second law has important implications. Clearly the distance between points 1 and 2 is shorter than the distance between points 3 and 4 in the figure below. Since the time interval is the same for these different distances, the planet is traveling at different velocities.

The velocity of a planet relative to the host star is derived by equating the gravitational force to the orbital acceleration. This velocity, \(v\), is given by the vis-viva equation 9.1.4:
\[v\,=\sqrt{GM(\frac{2}{r}\,-\frac{1}{a})}\]
where G is the gravitational constant: \(G\,=\,6.67408×10^{−11} m^3kg^{−1}s^{−2}\), \(r\) is the distance between the star and the planet, and \(a\) is the semi-major axis of the elliptical orbit.
The velocity of the planet in its orbit can easily be calculated at perihelion (or aphelion) by substituting the expression for rperihelion (or raphelion) into the vis-viva equation. In the case of a circular orbit, \(r=a\) and the velocity of a planet in a gravitationally bound orbit is constant and simplifies to:
\[v\,=\sqrt{\frac{GM}{R}}\]
where \(R\) is the radius of the circular orbit.
Kepler's Third Law
About a decade after Kepler had formulated his first two rules for the motion of planets in the solar system, he published a third law based on his empirical data, which says that the square of the orbital period is proportional to the cube of the semi-major axis:
\[P^2\propto a^3\]
where is the semi-major axis of the elliptical orbit and \(P\) is the orbital period.
This means that a planet that is closer to the Sun has a shorter orbital period than a planet that orbits farther away. Mercury completes one orbit in 88 days, Venus orbits in 225 days, and the Earth takes 365 days to travel around the Sun.
Kepler's third law can be used to find the orbital period or semi-major axis for planets in our solar system by dividing each side of equation 5.1.6 with values for the Earth.
\[\left(\frac{P_{Jup}}{P_{Earth}}\right) ^2\,=\left(\frac{a_{Jup}}{a_{Earth}}\right) ^3\]
The Earth has a 1 year orbital period and a semi-major axis defined as 1 Astronomical Unit (1 AU). Using those same dimensional units (years and AU) we can calculate the orbital period of Jupiter, which has a semi-major axis of 5.2 AU:
\[\left(\frac{P_{Jup}}{1\,year}\right) ^2\,=\left(\frac{a_{Jup}}{1\,AU}\right) ^3\]
\(P_{Jup}\,=\,11.86\,years\)

