5.10: X. Developing and Using Mathematical Representations to Estimate an Intriguing Quantity
- Page ID
- 15151
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)47
X. Developing and Using Mathematical Representations to Estimate an Intriguing Quantity
Emily van Zee and Elizabeth Gire
This section explores ways to visualize what happens as the Moon revolves around the Earth while the Earth is revolving around the Sun. Acting out such simultaneous motions can help make visible something surprising about what is happening. Drawing diagrams and developing mathematical representations can help answer intriguing questions that emerge from such visual representations of the simultaneous motions of the Moon and Earth.
A. Visualizing relationships among the Sun, Earth, and Moon through actions
1. Acting out the simultaneous motions of the Earth and the Moon
Equipment: Use the setup for modeling the Earth revolving around the Sun: put a lamp without a shade in the middle of the room, with cord taped to the floor to avoid students tripping over the cord. If possible, do this activity just before the Moon will be in its third quarter phase. It also can be adapted for use near the Moon’s first quarter phase.- Stand in pairs around the lamp representing the Sun. One person in each pair plays the role of the Earth. The other person in each pair plays the role of the Moon.
- Review the meanings of revolving and rotating.
- With the lamp turned off, rehearse how to act out the motion of the Earth during one week:
- About how far will the person representing an observer on Earth be moving in an orbit around the lamp?
- In what direction will the person representing “Earth” be revolving?
- In what direction with the person representing “Earth” be rotating?
- How many times will the person representing“Earth” be rotating to represent one week?
- With the lamp turned off, rehearse how to act out the motion of the Moon during one week:
- Where should the person playing the role of a full Moon stand with respect to the lamp and to the person representing an observer on Earth ?
- To where should the person representing a full Moon move to represent the third quarter Moon position?
- How will this person move to continue facing the person playing the role of an observer on Earth?
- Turn on the lamp. Sing or count day 1, day 2, day 3, day 4, day 5, day 6, day 7 while the person representing an observer on Earth and the person representing the Moon model the simultaneous motions of the Moon revolving around the Earth while the Earth revolves around the Sun while rotating on its axis during one week between the Moon’s full and third quarter phases.
- If you see a third quarter Moon, where are you and everyone else on Earth heading next?
2. Nuances in acting out the simultaneous motions of the Moon and the Earth
This kinesthetic activity engages participants in using their own motions to demonstrate what is happening. In particular, this activity can help distinguish more clearly between the specific meanings of revolving, in which one object orbits another object, and rotating, in which an object spins on its own axis.
The Earth does not move very far during one week compared to its total orbit around the Sun. There are about 52 weeks in one year, so the distance that the person playing the role of the Earth should move would be about 1/52 of the circumference of a circular orbit around the lamp. This is not very far – about a meter if the participants are moving in a circle about 10 meters away from the lamp. (Circumference/52 = 2πR/52 = 2*3*10 m/52 = a little over 1 meter.)
It is important to model accurately the direction of revolution and rotation. In the northern hemisphere, the person representing the Earth should revolvecounterclockwise around the lamp while rotating seven times counterclockwise in order to model the Earth’s motion during one week of seven days.
To start in the full Moon position, the person playing the role of the Moon should stand facing the person playing the role of the Earth in a line with the lamp as shown in Fig. 5.82.

As shown in Fig.5.83, when moving to the third quarter phase, the person playing the role of the Moon should move counterclockwise around the “Earth” until forming a right angle with the “Earth” and the lamp. The “Moon” should continue facing the “Earth” by also doing a quarter of a rotation while revolving

At the end of modeling the simultaneous motions of the Moon and the Earth between full moon and third quarter moon phases, the “Moon” person should be standing directly in the “Earth” person’s direction of travel around the lamp. The participants will have acted out a surprising finding:
When looking at a third quarter Moon, one is looking at the “place in space” where everyone on the Earth will soon “be” as the Earth revolves in its orbit around the Sun!
Acting out these simultaneous motions of the Earth and Moon can enhance students understanding of the difference between revolving and rotating motions as well as of the phenomena being modeled. Some students may remember the observations by a child visiting the southern hemisphere (Figs. 5.36 and 5.37) and wonder about what direction students in the opposite hemisphere would be revolving and rotating. Depending upon the time available and the level of understanding evident in class, exploring this issue may be feasible, particularly with a small group of students who like to pursue details that deepen their understandings.
The Sun and Moon appear to rise in the east and set in the west in both hemispheres. What is different is the direction one is looking when one sees the Moon, which is orbiting roughly in the plane of the equator (see Fig. 5.47).
In the northern hemisphere, the Sun and Moon appear mostly in the southern sky. When one looks south, east is on the left and west is on the right; therefore, both the Sun and Moon appear to move across the sky from left (east) to right (west) in the clockwise direction, as shown by the observation reported earlier in Fig. 5.8. In this case, the term clockwise reflects a geocentric model, with the Sun appearing to revolve daily around the Earth in a left to right, clockwise motion across the sky. Acting out the simultaneous motions of the Earth and Moon reflects a heliocentric model, however, with the lamp representing a fixed Sun and with the “Moon” revolving a quarter turn around the “Earth” and the “Earth” rotating seven times on an axis and revolving a short distance around the lamp, all in a counterclockwise direction.
In the southern hemisphere, the person representing the Earth should revolveclockwise around the lamp while rotating seven times clockwise to model the Earth’s motion during one week of seven days. To start in the full Moon position, the person playing the role of the Moon should stand facing the person playing the role of the Earth in a line with the lamp as in Fig. 5.82
When modeling moving to the third quarter phase, the person playing the role of the Moon should move clockwise around the “Earth” until forming a right angle to the lamp. The “Moon” should continue facing the “Earth” by also doing a quarter of a rotation while revolving.
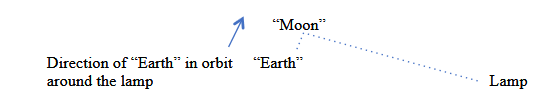
At the end of modeling the simultaneous motions of the Moon and the Earth between full moon and third quarter moon phases, the “Moon” person should be standing directly in the “Earth” person’s direction of travel around the lamp. The participants will have acted out the surprising finding that when looking at a third quarter Moon, one is looking at the “place in space” where everyone on the Earth will soon “be” as the Earth revolves in its orbit around the Sun!
In the southern hemisphere, the Sun and Moon mostly appear in the northern sky. When one is looking north, east is on the right and west on the left; both the Sun and Moon appear to move across the sky from right (east) to left (west) in a counterclockwise direction. In this case, the term counterclockwise reflects a geocentric model, with the Sun appearing to revolve daily around the Earth in a right to left motion across the sky. Acting out the simultaneous motions of the Earth and Moon reflects a heliocentric model, however, with the lamp representing a fixed Sun and with the “Moon” revolving a quarter turn around the “Earth” and the “Earth” rotating seven times on an axis and revolving a short distance around the lamp, all in clockwise direction.
B. Visualizing by drawing a diagram and thinking conceptually about the situation
Question 5.46 When you see a third quarter Moon, you are looking at the “place in space” where you and everyone else on Earth will soon “be”!
How soon will you get “there”?
- If you are looking at a third quarter Moon, how soon do you think you and everyone else on Earth will “be” at the “place is space” where a third quarter moon “is” now?
- Compare your estimate with those by your group members: are their estimates of the time required in minutes? hours? days? weeks? months?
- With your group members consider how you might calculate a numerical estimate:
- What can you draw to help visualize this situation?
- What are some central ideas that might be helpful in developing an equation with which to calculate an estimate of the time required for this ‘trip’?
- What quantities might be relevant to include in such an equation? What numerical values might be helpful to know?
- How can you use these insights to develop an equation and calculate an estimate?
1. Drawing a diagram that represents the situation and considering relevant central ideas
The following handout can guide development of a numerical estimate:
Where Are All of Us on Earth Heading Next?
Early one morning you see a third quarter moon.
Sketch a stick figure pointing one arm at the Sun and one arm at a 3rd quarter moon. About what time is this? (Sketch below is for someone in the northern hemisphere)_________________________________________
East S West
- What if you were able to look down on a third quarter moon from above the solar system?
- Sketch the Earth in its orbit around the Sun.
- Sketch the Moon in the third quarter position in its orbit around the Earth.
- Where are all of us on Earth heading next?
- When will we get there?
- Make an estimate based on your intuition
To make an estimate numerically:
- What do you know about the physics of this situation?
- What concepts, for example, are useful in describing motions?
- How are the distance traveled (∆ x) and the duration of a trip (∆t) related?
Use Δ (Greek letter delta) to represent “change in”:
-
- Δx is the change in position or distance traveled;
- Δt is the change in clock-reading or duration of the trip.
- What two assumptions would be helpful to make in this situation?
-
- About the Earth’s orbit?
- About the Earth’s speed in its orbit?
- What is the key relationship in this situation?
- Why is this equality justified?
- How can this equality be stated mathematically in words? In symbols?
- What is the equation (in symbols) for the unknown?
∆t =
- What numerical values do we know or are told?
Round numerical values to ease calculation when making an estimate:
∆x = average distance between Earth and Moon = 238,000 miles = about 250,000 miles
∆T = duration of one trip of Earth around Sun = one year = 365.25 days = about 400 days
R = distance from Earth to Sun = 93,000,000 miles = about 100,000,000 miles
Circumference of orbit = 2πR = distance Earth would travel in a circular orbit around the Sun
- How much time (∆t) would it take for the Earth to move in a circular orbit around the Sun from where the Earth is “now” to where the third quarter moon is “now”?
∆t =
- Is this a reasonable answer? Explain why.
2. Example of student work about the simultaneous motions of the Earth and Moon
As shown in FIG. 5.85, a student drew a sketch from the perspective of someone in the northern hemisphere who is looking south to see the Moon, with east on the left and west on the right. A third quarter moon is shown high in the sky with the Sun rising in the east at about 6 am. Two arrows represent the person forming a right angle by pointing one arm at the Sun and the other arm at the Moon, which is approximately half lit on the left.
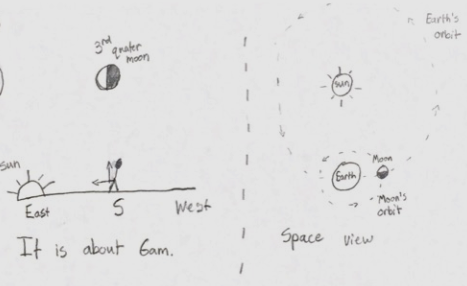
As shown on the right of Fig. 5.85, this student also drew a sketch of an inferred view from space from the perspective of looking down on the solar system from above. Dashes and arrows indicate the Earth revolving counterclockwise in its orbit around the Sun and the Moon revolving counterclockwise in its orbit around the Earth. The Moon, approximately half lit on the side facing the Sun, is shown in the 3rd quarter position, to the right of the Earth and located directly in the Earth’s orbit. If the Earth continues revolving counterclockwise around the Sun as shown, how soon will the Earth “be” in the “place in space” where the Moon “is” now? The student wrote:
The Earth will be headed to the point where the 3rd quarter moon is currently in…space. The Earth has a counterclockwise rotation (although true, the appropriate word should be “revolution” here) meaning it is moving right. To achieve the appearance of the third quarter moon, the moon has to be forming a 90-degree angle with Earth in respect to the sun. The moon must also be on the right side of the Earth as the left side of the moon appears lit by light from the sun.
A key concept needed to figure out how soon we will get there is the relationship between position, motion, and speed. If one knows their position, then they know the distance traveled and the amount of time it took to travel that distance. Knowing this it is possible to figure out how fast one got to that position or the speed they traveled…
The key relationship is the assumption that the speed of the time it takes to make one full orbit around the sun is the same speed it takes to travel from the earth’s current position to the position of the 3rd quarter moon.
The speeds can be set equal because (of the assumption that) the earth travels a constant speed when traveling its (assumed circular) orbit around the sun. The smaller journey is merely a section of that larger journey, but maintains that constant speed.
This relationship between the speeds leads to the equality that the distance of earth’s orbit over the time it takes to complete earth’s full orbit is equal to the distance to the 3rd quarter moon over the time it takes to reach the position of the 3rd quarter moon.
(Edits added in parentheses)
As shown in FIG. 5.86, this student wrote, in both words and symbols, the mathematics described above based on the assumption that the Earth is moving with constant speed in a circular orbit so that the speed for the total trip around the Sun is equal to the speed of the small trip from where the Earth “is” to where the third quarter Moon “is” now:
\[{\text{Total Trip Speed}} = {\text{Speed of Small Trip}}\]
The student stated this key relationship both in words and symbols:
\begin{split}{\text{In words:}}\\\\\frac{\text{Distance of Earth’s orbit}}{\text{Time of Earth’s orbit}} & = \frac{\text{Distance to the 3rd quarter moon}}{\text{Time to the 3rd quarter moon}} \\\\{\text{In symbols:}}\\\\ \frac{2 \pi R}{\Delta T} & = \frac{\Delta x}{∆t}\end{split}

The total distance traveled around the Earth’s assumed-to-be circular orbit would be its circumference, 2πR; ∆x represents the small distance traveled, the distance from where the Earth is and the “place in space” where the Moon is “now.”
The student used “Time of Earth’s orbit” to refer to the duration of the whole trip around the Sun and “Time to the 3rd Quarter moon” to refer to the duration of the short trip. This general language use of the word “time” can be separated into two distinct ideas: “duration” to refer to how long a trip lasts and “clock-reading” to refer to a particular instant, such as when a trip started or ended. In this case, “duration” is the meaning intended. The student used a capital T, ∆T, to refer to the duration of the entire trip around the Sun and a lower case t, ∆t, to refer to the duration of the short trip from where the Earth “is” to where the Moon “is” now.
Next the student solved this equation for the duration (∆t) for the small trip and substituted the estimated values provided. These had been rounded to make the calculation easy without needing a calculator:
∆t =
∆t =
Then the student reduced this equation to: ∆t =
and converted this to hours: ∆t = = 4 hours
to obtain an estimate of about 4 hours for the time for the Earth to move from where the Earth “is” to the “place in space” where the third quarter Moon “is” now.
Finally, as shown in Fig. 5.87, the student reflected upon the reasonableness of this answer:
I believe this answer is reasonable because when creating another equality which puts parts over wholes, it is equal. The equality is the distance to the 3rd quarter moon over the distance of earth’s rotation (should be revolution)equal to amount of time it takes to reach the 3rd quarter moon over the amount of time it takes to complete the earth’s orbit around the sun. When all the values are substituted in as they were for the original problem the values are equal to each other as shown below.
(Edit added in parentheses)

Physics Student, Winter 2018
Another student made sense of this answer in another way conceptually, by figuring out how far the Earth travels around the Sun in an hour and dividing that into the distance between the Earth and the Moon. This is similar to finding out how much time a 300 mile trip will take if one is traveling on a freeway at 60 miles/hour: (300 miles)/(60 mile/hour) = 5 hours.
I also did this problem using the distance the earth travels in a year, which is 584 million miles, and divided by 365 days to find out how far the earth travels in a day, I then divided this number by 24 to find out how far it travels in a hour. With this number I divided 238,900 miles, which is the distance to the moon, by the distance the earth travels in an hour to determine how many hours it takes the earth to move into the position of the moon. It was found that the earth takes about 4 hours to travel the distance to the moon.
This student apparently used some of the provided information, that the Earth is 93,000,000 miles from the Sun, as well as the assumption of a circular orbit, to estimate the total distance traveled around the Sun, 2πR, as 584,000,000 miles in one year of 365 days. The student next divided these numbers to find the distance traveled in one day, 584,000,000 miles/365 days = 1,600,109 miles/day (wow!) and divided by 24 hours to find the Earth’s orbital speed as 66,671 miles/hour. Then the student divided this number into the distance traveled from the Earth to the Moon: 238,900 miles/(66,671 miles/hour) = 3.58 hours. So about 4 hours is a reasonable answer, given the rounded numbers used.
Another way is to look up useful information on the Internet, such as the speed of the Earth in its orbit (https://astrosociety.org/edu/publications/tnl/71/howfast.html says 66,000 miles/hour), calculate how far the Earth would go at this speed in four hours, and compare that to the given average distance from the Earth to the Moon (238,000 miles).
(66,000 miles/hour)(4 hours) = 265,000 miles. This is high compared to the given average distance from the Earth to the Moon but close, given the rounded numbers provided.
An additional way would be to figure out how many of the short distances (from Earth to Moon) fit into the total distance around the Sun:
\[\frac{\text{Total distance around the Sun}}{\text{Distance from Earth to Moon}} = \frac{2 \pi R}{\Delta x}\]
Multiply this by the time obtained (∆t) and see if one gets a “year”
\[\frac{(2πR)(\Delta t)}{\Delta x} = \Delta T \, \text{(works symbolically if)} \frac{2\pi R}{\Delta T} = \frac{\Delta x}{\Delta t} \text{is solved for} \Delta T\]
Using the rounded values provided:
\[\frac{2 \pi (100,000,000 \, \text{miles})}{250,000 \, \text{miles}}\]
1 year = (about 400 days) (24 hours/day) = 9600 hours
3. Nuances about working on this question
Another student drew the following sketches on the handout as shown in Fig. 5.88:
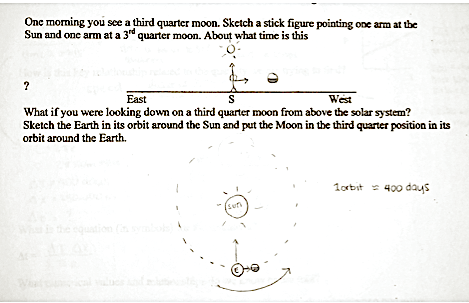
Although the problem statement included the phrase “one morning,” this student drew the Sun in the “noon” position with a setting third quarter Moon. “Noon” was the position suggested earlier for the Sun in the tables shown in Fig. 5.42 and 5.43 that present views of the phases of the moon as seen from Earth and from Space. The student also drew the view from space in the same way as shown in that table. The two views presented together here in Fig. 5.88 nicely review the connection that the angle formed by pointing one’s arms at the Sun and Moon on Earth is the same as the angle formed by the arrangement of the Sun, Earth, and Moon in space.
The reason that this activity suggests sketching the view from Earth in the morning rather than at noon is that this choice emphasizes that a third quarter Moon is readily visible high in the sky at about 6 am, and will continue to be visible throughout the morning if the sky is clear. If one wants to see such a moon, morning is a good time to look! Also our course meets during the morning, so if the sky is clear, the students can go outside and see a third quarter Moon in the “place in space” where they and everyone else on Earth soon will “be.”
This activity also reviews the details expected in sketching such diagrams. This student correctly drew the Sun and the Moon about the same size as seen from Earth but with a large Sun, small Earth, and smaller Moon as seen from space. In both diagrams the moon is shown half lit, with the lit portion facing the Sun. The view from space shows an assumed circular orbit, with a large arrow indicating the counterclockwise direction of the Earth’s revolution around the Sun and a small arrow indicating the Earth’s movement toward the third quarter Moon along this orbital path as seen from the northern hemisphere. The arrow pointing from the Earth toward the Sun might be confusing, however, if a viewer interpreted it as indicating a motion by the Earth directly toward the Sun.
The format of the handout mirrors the problem-solving processes advocated earlier in weeks 2 and 4 for pinhole math and thermal math problems:
Describe a scenario in words
Make a sketch of the situation
Review any relevant central ideas that you know
Draw a careful diagram if needed
Represent the scenario mathematically
State and justify an equation in words
Define symbols and state the equation in symbols
Solve for the unknown in symbols
Record given values and estimate any needed
Substitute values and calculate answer
Check and reflect on answer
Checking an answer can take many forms; particularly encouraged is seeking a conceptually different approach from that used for the calculation. Such sense-making is more likely to suggest an alternative approach if further thinking is needed.

