1.2.3: Increasing and Decreasing Functions
- Page ID
- 14129
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Increasing and Decreasing
It is important to be able to distinguish between when functions are increasing and when they are decreasing. In business this could mean the difference between making money and losing money. In physics it could mean the difference between speeding up and slowing down.
How do you decide when a function is increasing or decreasing?
Increasing and Decreasing Functions
Increasing means places on the graph where the slope is positive.
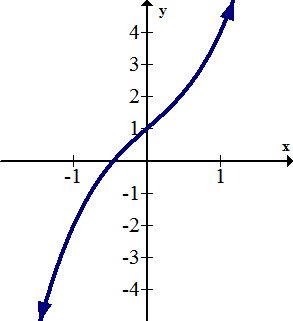 [Figure1]
[Figure1]The formal definition of an increasing interval is: an open interval on the x axis of (a,d) where every b,c∈(a,d) with b<c has f(b)≤f(c).
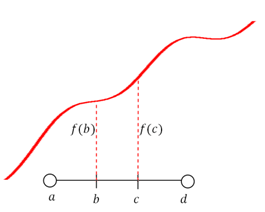 [Figure2]
[Figure2]A interval is said to be strictly increasing if f(b)<f(c) is substituted into the definition.
Decreasing means places on the graph where the slope is negative. The formal definition of decreasing and strictly decreasing are identical to the definition of increasing with the inequality sign reversed.
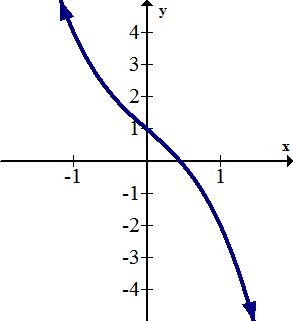 [Figure3]
[Figure3]A function is called monotonic if the function only goes in one direction and never switches between increasing and decreasing.
Out of the basic functions, the monotonically increasing functions are:
\(\ f(x)=x, f(x)=x^{3}, f(x)=\sqrt{x}, f(x)=e^{x}, f(x)=\ln x, f(x)=\frac{1}{1+e^{-x}}\)
The only basic functions that are not monotonically increasing are:
\(\ f(x)=x^{2}, f(x)=|x|, f(x)=\frac{1}{x}, f(x)=\sin x\)
Identifying analytically where functions are increasing and decreasing often requires Calculus. For PreCalculus, it will be sufficient to be able to identify intervals graphically and through your knowledge of what the parent functions look like.
Examples
Solution
Earlier, you were asked how to determine if a function is increasing or decreasing. Increasing is where the function has a positive slope and decreasing is where the function has a negative slope. A common misconception is to look at the squaring function and see two curves that symmetrically increase away from zero. Instead, you should always read functions from left to right and draw slope lines and decide if they are positive or negative.
Estimate where the following function is increasing and decreasing.
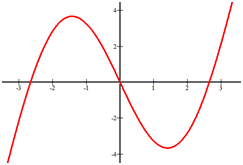 [Figure4]
[Figure4]Solution
Increasing: x∈(−∞,−1.5)∪(1.5,∞).
Decreasing: x∈(−1.5,1.5)
Estimate where the following function is increasing and decreasing.
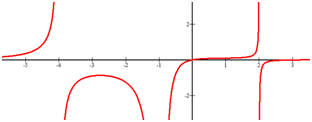 [Figure5]
[Figure5]Solution
Increasing x∈(−∞,−4)∪(−4,−2.7)∪(−1,2)∪(2,∞).
Decreasing x∈(−2.7,−1)
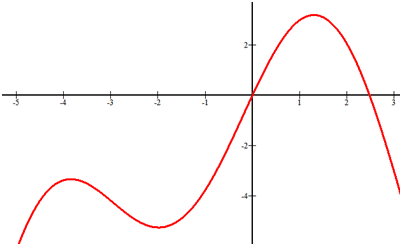
Estimate the intervals where the function is increasing and decreasing.
 [Figure6]
[Figure6]Solution
Increasing: x∈(−∞,−4)∪(−2,1.5)
Decreasing: x∈(−4,−2)∪(1.5,∞)
Notice that open intervals are used because at x=−4,−2,1.5 the slope of the function is zero. This is where the slope transitions from being positive to negative. The reason why open parentheses are used is because the function is not actually increasing or decreasing at those specific points.
A continuous function has a global maximum at the point (3, 2), a global minimum at (5, -12) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?
Solution
Increasing x∈(−∞,3)∪(5,∞).
Decreasing x∈(3,5)
Note: The y coordinates are not used in the intervals. A common mistake is to want to use the y coordinates.
Review
Use the graph below for 1-2.
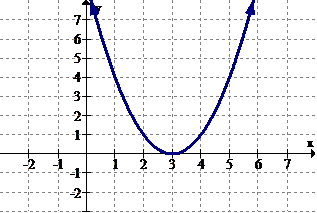 [Figure7]
[Figure7]1. Identify the intervals (if any) where the function is increasing.
2. Identify the intervals (if any) where the function is decreasing.
Use the graph below for 3-4.
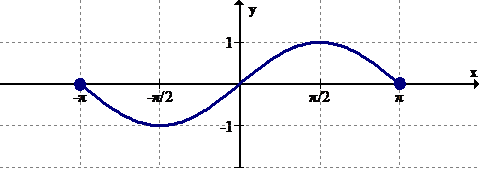 [Figure8]
[Figure8]3. Identify the intervals (if any) where the function is increasing.
4. Identify the intervals (if any) where the function is decreasing.
Use the graph below for 5-6.
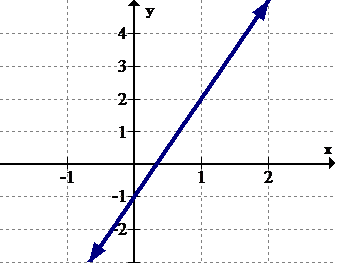 [Figure9]
[Figure9]5. Identify the intervals (if any) where the function is increasing.
6. Identify the intervals (if any) where the function is decreasing.
Use the graph below for 7-8.
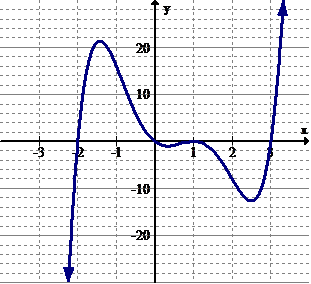 [Figure10]
[Figure10]7. Identify the intervals (if any) where the function is increasing.
8. Identify the intervals (if any) where the function is decreasing.
Use the graph below for 9-10.
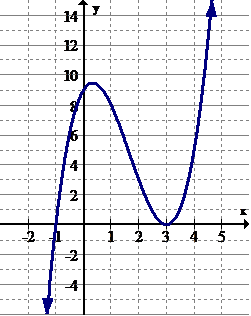 [Figure11]
[Figure11]9. Identify the intervals (if any) where the function is increasing.
10. Identify the intervals (if any) where the function is decreasing.
11. Give an example of a monotonically increasing function.
12. Give an example of a monotonically decreasing function.
13. A continuous function has a global maximum at the point (1, 4), a global minimum at (3, -6) and has no relative extrema or other places with a slope of zero. What are the increasing and decreasing intervals for this function?
14. A continuous function has a global maximum at the point (1, 1) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?
15. A continuous function has a global minimum at the point (5, -15) and has no other extrema or places with a slope of zero. What are the increasing and decreasing intervals for this function?
Vocabulary
| Term | Definition |
|---|---|
| Continuous | Continuity for a point exists when the left and right sided limits match the function evaluated at that point. For a function to be continuous, the function must be continuous at every single point in an unbroken domain. |
| Function | A function is a relation where there is only one output for every input. In other words, for every value of x, there is only one value for y. |
| Global Maximum | The global maximum of a function is the largest value of the entire function. Symbolically, it is the highest point on the entire graph. |
| Global Minimum | The global minimum of a function is the smallest value of the entire function. Symbolically, it is the lowest point on the entire graph. |
| increasing | A function is increasing over an interval if its y values are getting larger over the interval. The graph will go up from left to right over the interval. |
| Interval Notation | Interval notation is the notation [a,b), where a function is defined between a and b. Use ( or ) to indicate that the end value is not included and [ or ] to indicate that the end value is included. Never use [ or ] with infinity or negative infinity. |
| monotonic | A function is monotonic if it does not switch between increasing and decreasing at any point. |
| relative extrema | The relative extrema of a function are the points of the function with y values that are the highest or lowest of a local neighborhood of the function. |
| strictly | Strictly is an adjective that alters increasing and decreasing to exclude any flatness or periods where y values are staying constant. |
Image Attributions
- [Figure 1]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 2]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 3]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 4]
Credit: CK-12 Foundation
Source: https://www.flickr.com/photos/davidstanleytravel/8227858392/in/photolist-dx4VDs-nKC9j9-My5FPU-9rfFDj-rXVj6c-G9QvSn-FTuBdG-NVoCS3-8qRnga-4ykGxj-jeRZix-Nm65u9-MuS8RM-MtrYpq-nRand5-LSSMHM-GjMCi9-aaGbZM-opao7s-2Cact-FbjHE8-5nGfWn-pniMjM-6C6LQc-xzgo7p-4jAyjp-dQwCx8-Nh11cH-qrnGo4-qq1pzb-j5K9gk-9Pu1uQ-8BxKVf-5J85eG-j5LBAg-cfh4yL-5nLVFj-jeTveb-PSNJ1-K2fTUM-sngP1k-dBmaU6-hMPbWH-pk7mb-6R8PPi-ab6auH-KzX648-4oyMEc-9NHJGZ-Ny57L3
License: CC BY-SA - [Figure 5]
Credit: CK-12 Foundation
Source: https://www.flickr.com/photos/davidstanleytravel/8227858392/in/photolist-dx4VDs-nKC9j9-My5FPU-9rfFDj-rXVj6c-G9QvSn-FTuBdG-NVoCS3-8qRnga-4ykGxj-jeRZix-Nm65u9-MuS8RM-MtrYpq-nRand5-LSSMHM-GjMCi9-aaGbZM-opao7s-2Cact-FbjHE8-5nGfWn-pniMjM-6C6LQc-xzgo7p-4jAyjp-dQwCx8-Nh11cH-qrnGo4-qq1pzb-j5K9gk-9Pu1uQ-8BxKVf-5J85eG-j5LBAg-cfh4yL-5nLVFj-jeTveb-PSNJ1-K2fTUM-sngP1k-dBmaU6-hMPbWH-pk7mb-6R8PPi-ab6auH-KzX648-4oyMEc-9NHJGZ-Ny57L3
License: CC BY-SA - [Figure 6]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 7]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 8]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 9]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 10]
Credit: CK-12 Foundation
License: CC BY-SA - [Figure 11]
Credit: CK-12 Foundation
License: CC BY-SA

