3.2: Continuity at a Point, Continuity Test, Types of Discontinuity
- Page ID
- 1195
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the previous concept, the continuity of a function was presented intuitively through the imagery of using a pencil to draw a graph on a piece of paper (over a certain interval of the domain) and never lifting the pencil off the paper. As long as the pencil is not lifted off the paper, the graph can be considered to be continuous over that drawing interval. This is certainly not a rigorous description of continuity, but given this analogy, what expectations might you have about arithmetic operations on two functions that are both continuous over a common interval; or the existence of minima and maxima of a continuous function; or the existence of intermediate values between two function values?
Properties of Continuous Functions
The previous concept identified the characteristics of a function that is continuous at a point, and over an interval. Let’s explore Given two functions f(x) and g(x) that are continuous over a closed interval [a,b], would you expect that arithmetic operations on these two functions would also yield functions continuous over [a,b]?
Given the functions f(x)=x+3 and g(x)=−x+0.5 in the closed interval [−1,1], determine if f(x) and g(x) are continuous in the interval.
The functions f(x) and g(x) are shown in the graph. Inspection of each function graph and its equation, shows that they are each defined over the closed interval and the function limit at each point in the interval equals the function value at the point. Both functions are continuous in the interval.
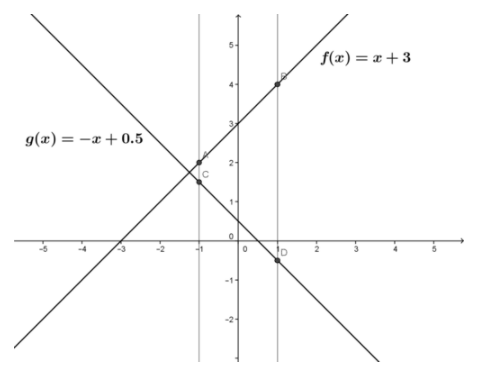
CK-12 Foundation - CC BY-NC-SA
Using the same functions and interval as above, determine if h(x)=f(x)+g(x) is continuous in the interval.
The sum of the two functions is given by h(x)=3.5, and is shown in the figure. The sum function, a constant, is defined over the closed interval and the function limit at each point in the interval equals the constant function value at each point. The sum function is continuous in the interval.
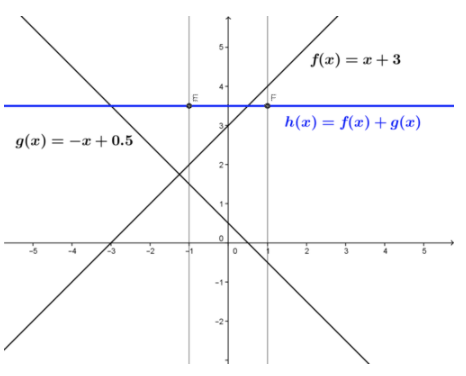
CK-12 Foundation - CC BY-NC-SA
Still using the interval and functions as above, determine if h(x)=f(x)g(x) is continuous in the interval.
The product of the two functions is given by h(x)=(x+3)(−x+0.5)=−x2+2.5x−1.5, and is shown in the figure. The product function, a parabola, is defined over the closed interval and the function limit at each point in the interval equals the product function value at each point. The product function is continuous in the interval.
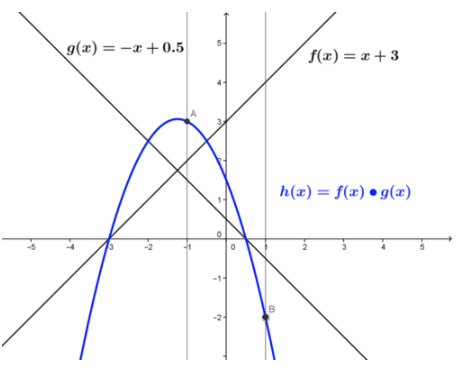
CK-12 Foundation - CC BY-NC-SA
What about the quotient of two continuous functions?
Given the functions f(x)=x+3 and g(x)=−x+0.5 in the closed interval [−1,1], determine if f(x)/g(x) is continuous in the interval.
The quotient of the two functions is given by
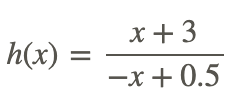
and is shown in the figure.
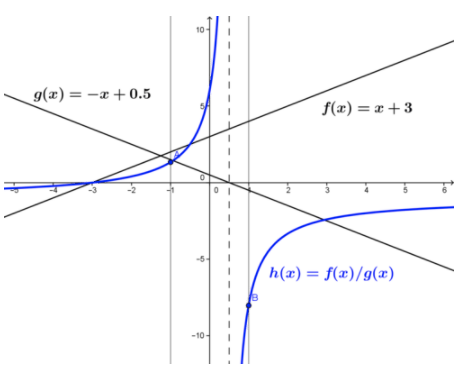
CK-12 Foundation - CC BY-NC-SA
In the closed interval [−1,1], x=0.5 is the only place where the function h(x) is undefined, and
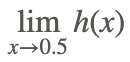
r in the closed interval.
The findings in the above simple functions can be generalized in the following properties.
If f(x) and g(x) are continuous at any real value c over the closed interval [a,b], then the following are also continuous at any real value c over the closed interval [a,b]:
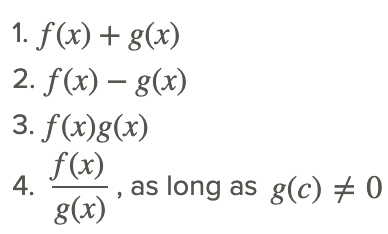
Intermediate Value Theorem and the Extreme Value (Min-Max) Theorem are two other properties of a function that is continuous over a closed interval.
The Intermediate Value Theorem and Extreme Value Theorem
The Intermediate Value Theorem states that if a function is continuous on a closed interval [a,b], then the function assumes every value between f(a) and f(b).
The Intermediate Value Theorem can be used to analyze and approximate zeros of functions.
Use the Intermediate Value Function to show that there is at least one zero of the function f(x)=3x4−3x3−2x+1 in the indicated interval [1,2].
The graph of this function, shown below, is shaped somewhat like a parabola, and is continuous in the interval.
CC BY-NC-SA
In order to apply the Intermediate Value Theorem, we need to find a pair of x-values that have function values with different signs. A few values are shown in the table below.
|
x |
1.1 |
1.2 |
1.3 |
|
f(x) |
-0.80 |
-0.36 |
0.37 |
We see that the sign of the function values changes from negative to positive somewhere between 1.2 and 1.3. Hence, by the Intermediate Value theorem, there is some value c in the interval (1.2, 1.3) such that f(c)=0.
The Extreme Value (Min-Max Theorem) is a consequence of the Intermediate Value Theorem.
The Extreme Value (Min-Max) Theorem states that if a function f(x) is continuous in a closed interval I, then f(x) has both a maximum value and a minimum value in I.
Examples
Example 1
Earlier, you were asked about your expectations for the continuity of functions formed by arithmetic operations on two continuous functions. The conclusion of this section is that, except for the quotient of functions, arithmetic operations on two functions that are continuous at a point or in an interval yield a new function that is continuous at the point or in the interval. With the quotient of two functions, the concern is always to identify where the denominator is 0; at this location the quotient function is not continuous.
Example 2
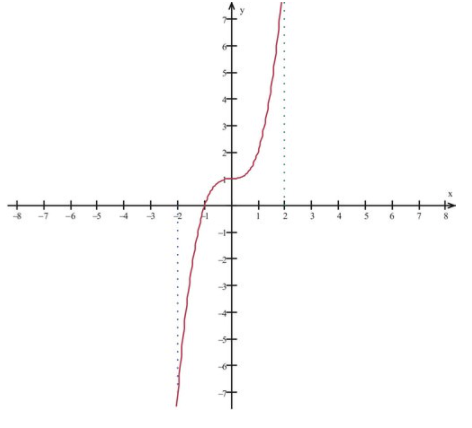
Consider f(x)=x3+1 and interval I=[−2,2]. Determine minimum and maximum values.
Since the function is continuous on the closed interval I, this function has a minimum and a maximum on the interval. The function graph shows that at x=−2 the function has a minimum value f(−2)=−7; and at x=2, a maximum value f(2)=9.
CC BY-NC-SA
Review
For #1-5, explain how you know that the function has a root in the given interval. (Hint: Use the Intermediate Value Function to show that there is at least one zero of the function in the indicated interval.):
- f(x)=x3+2x2−x+1, in the interval [-3,-2].
- f(x)=x.5−x√3−1, in the interval [9,10].
- f(x)=x2+x−2, in the interval [-3,0].
- f(x)=4x2−1x2+3x+2, in the interval [-1,0].
- f(x)=2x+3−4, in the interval [-3,0].
- True or False: f(x)=sin(x)+cos(x) has a root on the interval [0,π].
- True or False: By the Intermediate Value Theorem f(x)=sin(x)+cos2(x) has no root on the interval [0,π] since f(0)=f(π)=1.
- True or False: f(x)=x2+1cos(x) has a root on the interval [0,π].
- On which interval is f(x)=x−sin(x)+1 guaranteed by the IVT to have a root?
10. Find an interval on which f(x)=ex+x has a root.
11. Find intervals on which f(x)=x3+5x2−4x−20 has a root.
For #12-15, use the Extreme Value Theorem to determine whether the given statement is true or false.
- The Extreme Value Theorem guarantees that the function |sin(x3)|0.5 has a minimum value on the interval [-3, 3].
- The Extreme Value Theorem guarantees that the function (x−1)3 has a maximum value on the interval [1, 3].
- The Extreme Value Theorem guarantees that the function x2+3x+2 has a minimum value on the interval [-3, 0].
- The Extreme Value Theorem guarantees that the function 4x/x2+3x+2 has a minimum value on the interval [-3, 0].
Vocabulary
| Term | Definition |
|---|---|
| Continuous | Continuity for a point exists when the left and right sided limits match the function evaluated at that point. For a function to be continuous, the function must be continuous at every single point in an unbroken domain. |
| Continuous Function | A continuous function is a function without breaks or gaps. It contains an infinite, uncountable number of values. |
| discontinuous at a point | A function is discontinuous at a point a if the function is not defined at x=a. |
| extreme value theorem | The extreme value theorem states that in every interval [a,b] where a function is continuous there is at least one maximum and one minimum. In other words, it must have at least two extreme values. |
| intermediate value theorem | The intermediate value theorem states that if f(x) is continuous on some interval [a,b] and n is between f(a) and f(b), then there is some c∈[a,b] such that f(c)=n. |
| points of discontinuity | The points of discontinuity for a function are the input values of the function where the function is discontinuous. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - Properties of Continuous Functions
Video: Continuity and the Intermediate Value Theorem
Practice: Continuity at a Point, Continuity Test, Types of Discontinuity
Real World: New Orbits

