1.5: Midpoint Formula
- Page ID
- 2119
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determine the midpoints of line segments by taking the average of \(x\) values and average of \(y\) values
Suppose a coordinate plane were transposed over a subway map, and the blue line went in a straight line from the point \(\left(-9, 8\right)\) to the point \(\left(1, -4\right)\). If you got on the blue line at the beginning of the line and traveled halfway to the end of the line, what would be your coordinates? How would you calculate these coordinates?
Consider the following situation: You live in Des Moines, Iowa and your grandparents live in Houston, Texas. You plan to visit them for the summer and your parents agree to meet your grandparents halfway to exchange you. How do you find this location?
By meeting something “halfway,” you are finding the midpoint of the straight line connecting the two segments. In the above situation, the midpoint would be halfway between Des Moines and Houston.
The midpoint between two coordinate pairs represents the halfway point, or the average. It is the ordered pair \(\left(x_m, y_m\right)\) where:
\(\left(x_m,y_m\right)=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
Let's find the location that's halfway between Des Moines and Houston given the information from above:
Des Moines, Iowa has the coordinates \(\left(41.59, 93.62\right)\).
Houston, Texas has the coordinates \(\left(29.76, 95.36\right)\).
Find the coordinates of the midpoint between these two cities.
Decide which ordered pair will represent
\(\left(x_1, y_1\right)\) and which will represent \(\left(x_2, y_2\right)\).
\(\left(x_1, y_1\right )=\left(41.59,93.62\right)\)
\(\left(x_2, y_2\right)=\left(29.76,95.36\right)\)
Compute the midpoint using the formula
\(\left(x_m,y_m\right )=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
\(\left(x_m,y_m\right )=\left(\dfrac{41.59+29.76}{2} , \dfrac{93.62+95.36}{2}\right)\)
\(\left(x_m,y_m\right)=\left (35.675,94.49\right)\)
Using Google Maps, you can meet in the Ozark National Forest, halfway between the two cities.
Now, let's complete the following problems using the midpoint formula:
- A segment with endpoints \(\left(9, –2\right)\) and \(\left(x_1, y_1\right)\) has a midpoint of \(\left(2, –6\right)\). Find \(\left(x_1, y_1\right)\).
Use the Midpoint Formula:
\(\dfrac{x_1+x_2}{2}=x_m\)
\(2=\dfrac{x_1+9}{2} \rightarrow 4=x_1+9\)
\(x_1 = -5\)
Following the same procedure:
\(\dfrac{y_1+(−2)}{2} = −6 \rightarrow y_1+(−2)=−12\)
\(y_1=−10\)
\(\left(x_1,y_1)=(−5,−10\right)\)
- Find the values of x and y that make \(\left(9.5,6\right)\) the midpoint of \(\left(3,5\right)\) and \(\left(x,y\right)\).
Start with the formula, and solve for the variables:
The midpoint formula: \(\left(x_m, y_m\right )=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\)
Substitute in the given values and variables: \(\left(9.5,6\right)=\left(\dfrac{3+x}{2}, \dfrac{5+y}{2}\right)\)
This can be re-written as two equations:
\(9.5=\dfrac{3+x}{2}\); \(6=\dfrac{5+y}{2}\)
Multiply each side by 2: \(19=3+x\); \(12=5+y\)
Isolate the variables: \(16=x\); \(7=y\)
Example \(\PageIndex{1}\)
Earlier, you were asked to calculate your coordinates after traveling halfway to the end of the subway's blue line. You know that that the blue line goes in a straight line from \(\left(-9,8\right)\) to the point \(\left(1, -4\right)\).
Solution
To calculate these coordinates, you need to calculate the midpoint between \(\left(-9,8\right)\) and \(\left(1, -4\right)\).
To find the midpoint between \(\left(-9,8\right)\) and \(\left(1, -4\right)\), substitute in the given values into the midpoint formula and solve.
The midpoint formula: \(\left(x_m,y_m\right)=\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\)
Substitute in the given values and variables: \(midpoint=\left(\dfrac{-9+1}{2} , \dfrac{8+(-2)}{2}\right)\)
\(midpoint=\left(−4,2\right)\)
Therefore, the coordinates of the subway train halfway down the blue line are \(\left(-4, 2\right)\).
Example \(\PageIndex{2}\)
On a hike, you and your friend decide to take different routes, but then meet up for lunch. You hike 3 miles north and 2 miles west. Starting from the same point, your friend hikes 4 miles east and 1 mile south. From these points, you each walk towards each other, meeting halfway for lunch. Where would your lunchtime meeting place be in reference to your starting point?
Solution
Think of the starting point as the origin of a Cartesian coordinate system. If you walk north 3 miles, that is walking straight up the graph 3 units. Walking west 2 miles is the same as walking left 2 units on the graph. Then you have arrived at the point \(\left(-2, 3\right)\). For your friend, east is to the right (positive) and south is down (negative), so he/she arrives at \(\left(4,-1\right)\). Now you need to find the midpoint:
\(\left(x_m,y_m\right)=\left(\dfrac{-2+4}{2} , \dfrac{3+(-12)}{2}\right)=(22,22)=\left(1,1\right)\)
Your lunch time meeting place would be 1 mile north and 1 mile east of your starting point.
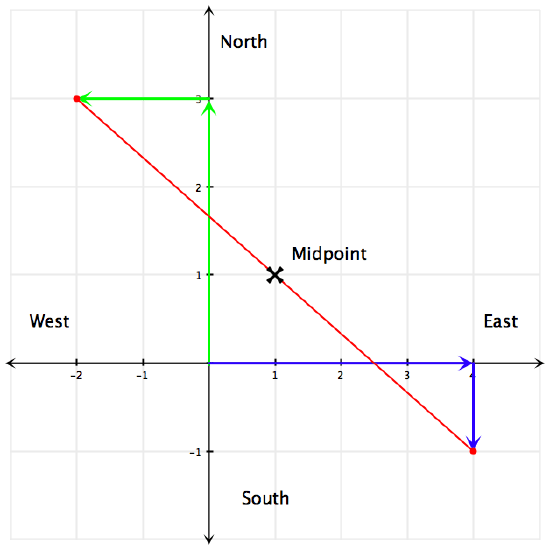Figure \(\PageIndex{1}\)Review
In 1–10, find the midpoint of the line segment joining the two points.
- \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\)
- \(\left(7, 7\right)\) and \(\left(–7, 7\right)\)
- \(\left(–3, 6\right)\) and \(\left(3, –6\right)\)
- \(\left(–3, –1\right)\) and \(\left(–5, –8\right)\)
- \(\left(3, –4\right)\) and \(\left(6, 1\right)\)
- \(\left(2, –3\right)\) and \(\left(2, 4\right)\)
- \(\left(4, –5\right)\) and \(\left(8, 2\right)\)
- \(\left(1.8, –3.4\right)\) and \(\left(–0.4, 1.4\right)\)
- \(\left(5, –1\right)\) and \(\left(–4, 0\right)\)
- \(\left(10, 2\right)\) and \(\left(2, –4\right)\)
- An endpoint of a line segment is \(\left(4, 5\right)\) and the midpoint of the line segment is \(\left(3, –2\right)\). Find the other endpoint.
- An endpoint of a line segment is \(\left(–10, –2\right)\) and the midpoint of the line segment is \(\left(0, 4\right)\). Find the other endpoint.
- Shawn lives six blocks west and ten blocks north of the center of town. Kenya lives fourteen blocks east and two blocks north of the center of town.
- How far apart are these two girls “as the crow flies”?
- Where is the halfway point between their houses?
Mixed Review
- A population increases by 1.2% annually. The current population is 121,000.
- What will the population be in 13 years?
- Assuming this rate continues, when will the population reach 200,000?
- Write \(1.29651843 \cdot 10^5\) in standard form.
- Is \(4, 2, 1,\dfrac{1}{2}, \dfrac{1}{6}, \dfrac{1}{8}, …\) an example of a geometric sequence? Explain your answer.
- Simplify \(6x^3(4xy^{2}+y^{3}z)\).
- Suppose \(0=(x−2)(x+1)(x−3)\). What are the \(x\)−intercepts?
- Simplify \(\sqrt{300}\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.8.
Vocabulary
| Term | Definition |
|---|---|
| Midpoint Formula | The midpoint formula says that for endpoints \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\), the midpoint is \(\left(\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right)\). |
| midpoint | The midpoint of two vectors is the location in the center of their endpoints. |
Additional Resource
Interactive Element
Video: Midpoint Formula - Overview
Activities: Midpoint Formula Discussion Questions
Practice: Midpoint Formula
Real World: SF Map - PythThm