1.1: Geometry Terms

Define and use terms, including points, lines, planes, space, and postulates.

Geometric Definitions

A point is an exact location in space. It describes a location, but has no size. Examples are shown below:

Figure \(\PageIndex{1}\)

Table 1.1.1

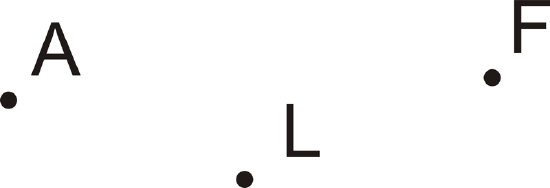
Label It	Say It
\(A\)	point \(A\)

A line is infinitely many points that extend forever in both directions. Lines have direction and location and are always straight.

Figure \(\PageIndex{2}\)

Table 1.1.2

Label It	Say It
line \(g\)	line \(g\)
\(\overleftrightarrow{PQ}\)	line \(PQ\)

A plane is a flat surface that contains infinitely many intersecting lines that extend forever in all directions. Think of a plane as a huge sheet of paper with no thickness that goes on forever.

Figure \(\PageIndex{3}\)

Table 1.1.3

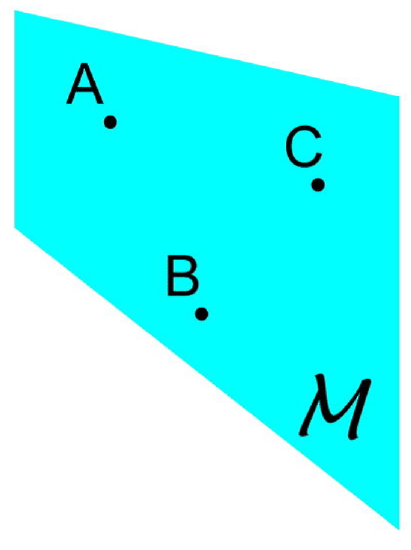
Label It	Say It
Plane \(M\)	Plane \(M\)
Plane \(ABC\)	Plane \(ABC\)

We can use point, line, and plane to define new terms.

Space is the set of all points extending in three dimensions. Think back to the plane. It extended in two dimensions, what we think of as up/down and left/right. If we add a third dimension, one that is perpendicular to the other two, we arrive at three-dimensional space.

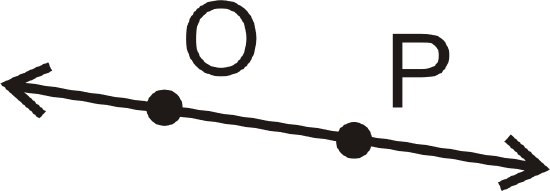
Points that lie on the same line are collinear. \(P\),\(Q\),\(R\),\(S\), and \(T\) are collinear because they are all on line \(w\). If a point U were located above or below line w, it would be non-collinear.

Figure \(\PageIndex{4}\)

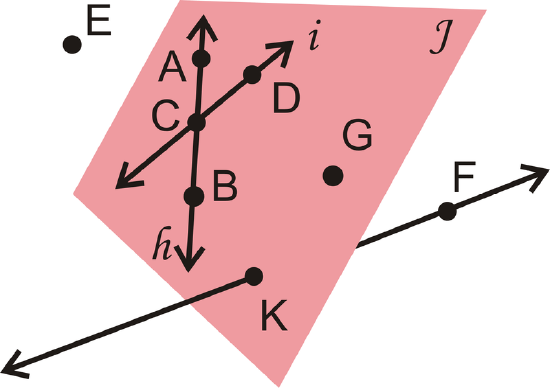
Points and/or lines within the same plane are coplanar. Lines h and i, and points \(A\),\(B\),\(C\),\(D\),\(G\), and \(K\) are coplanar in Plane \(J\). Line \(\overleftrightarrow{KF}\) and point \(E\) are non-coplanar with Plane \(J\).

Figure \(\PageIndex{5}\)

An endpoint is a point at the end of a line segment. A line segment is a portion of a line with two endpoints. Or, it is a finite part of a line that stops at both ends. Line segments are labeled by their endpoints. Order does not matter.

Figure \(\PageIndex{6}\)

Table 1.1.4

Label It	Say It
\(\overline{AB}\)	Segment \(AB\)
\(\overline{BA}\)	Segment \(BA\)

A ray is a part of a line. It begins with an endpoint and extends forever away from the endpoint in one direction, perfectly straight. A ray is labeled by its endpoint and one other point on the ray. For rays, order does matter. When labeling, put the endpoint under the side WITHOUT the arrow.

Figure \(\PageIndex{7}\)

Table 1.1.5

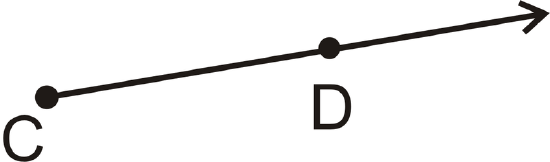
Label It	Say It
\(\overrightarrow{CD}\)	Ray \(CD\)
\(\overleftarrow{DC}\)	Ray \(CD\)

An intersection is a point or set of points where lines, planes, segments, or rays overlap.

Figure \(\PageIndex{8}\)

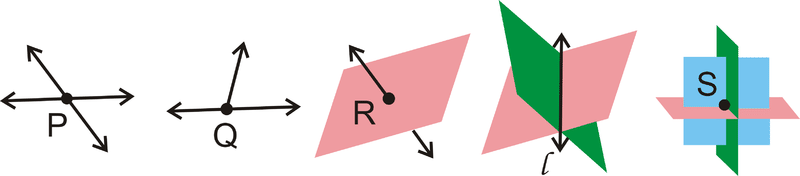
Postulates

A postulate is a basic rule of geometry. Postulates are assumed to be true (rather than proven), much like definitions. The following is a list of some basic postulates.

Postulate #1: Given any two distinct points, there is exactly one (straight) line containing those two points.

Figure \(\PageIndex{9}\)

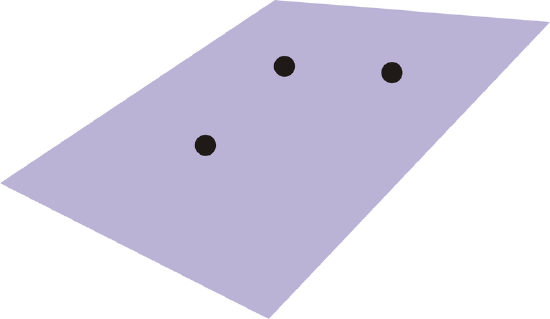
Postulate #2: Given any three non-collinear points, there is exactly one plane containing those three points.

Figure \(\PageIndex{10}\)

Postulate #3: If a line and a plane share two points, then the entire line lies within the plane.

Figure \(\PageIndex{11}\)

Postulate #4: If two distinct lines intersect, the intersection will be one point.

Figure \(\PageIndex{12}\)

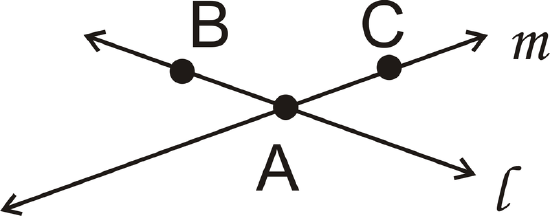
Lines \(I\) and \(m\) intersect at point \(A\).

Postulate #5: If two distinct planes intersect, the intersection will be a line.

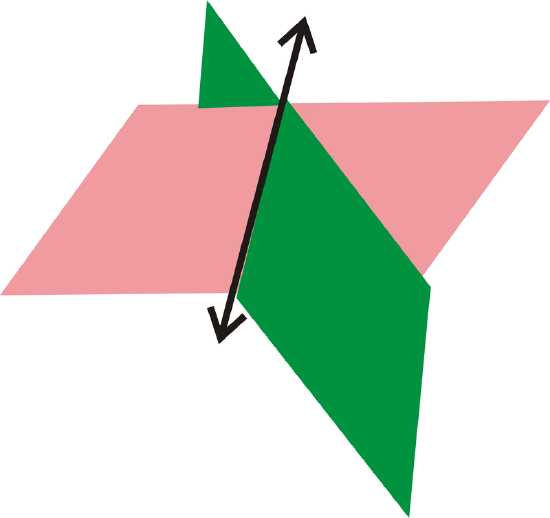
Figure \(\PageIndex{13}\)

When making geometric drawings, be sure to be clear and label all points and lines.

What if you were given a picture of a figure or object, like a map with cities and roads marked on it? How could you explain that picture geometrically?

Example \(\PageIndex{1}\)

What best describes San Diego, California on a globe: point, line, or plane?

Solution

A city is usually labeled with a dot, or point, on a globe.

Example \(\PageIndex{2}\)

Use the picture below to answer these questions.

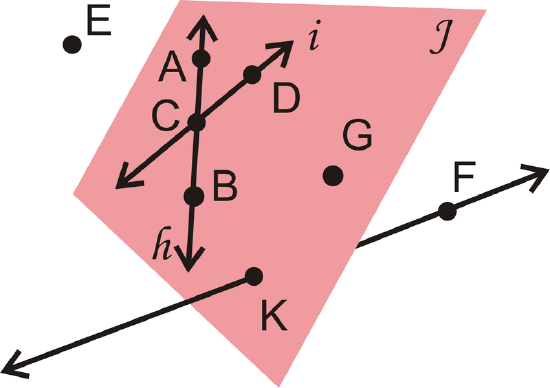
Figure \(\PageIndex{14}\)

1. List another way to label Plane \(J\).
2. List another way to label line \(h\).
3. Are \(K\) and \(F\) collinear?
4. Are \(E\),\(B\) and \(F\) coplanar?

Solution

1. Plane \(BDG\) is one possibility. Any combination of three coplanar points that are not collinear would be correct.
2. \(\overleftrightarrow{AB}\). Any combination of two of the letters \(A\), \(B\), or \(C\) would also be correct.
3. Yes, they both lie on \(\overleftrightarrow{KF}\).
4. Yes, even though \(E\) is not in Plane \(J\), any three points make a distinct plane. Therefore, the three points create Plane \(EBF\).

Example \(\PageIndex{3}\)

What best describes a straight road that begins in one city and stops in a second city: ray, line, segment, or plane?

Solution

The straight road connects two cities, which are like endpoints. The best term is segment.

Example \(\PageIndex{4}\)

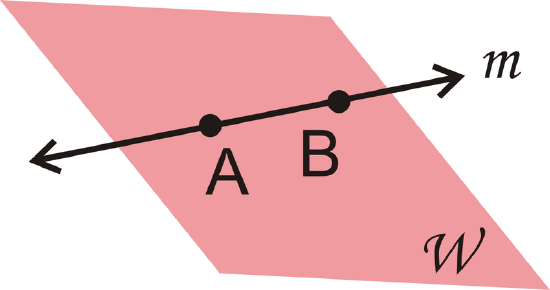
Answer the following questions about the picture.

Figure \(\PageIndex{15}\)

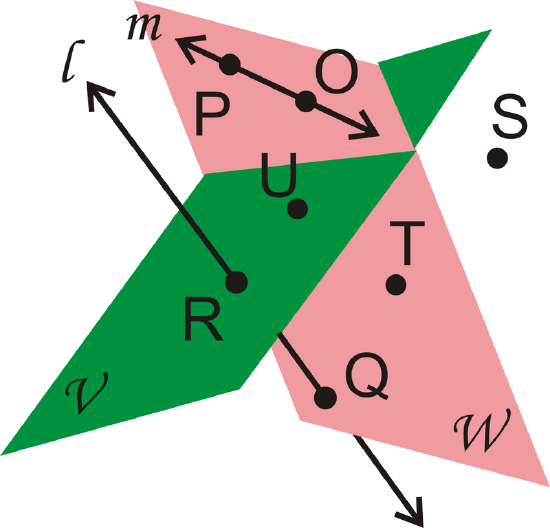
1. Is line \(l\) coplanar with Plane \(V\), Plane \(W\), both, or neither?
2. Are \(R\) and \(Q\) collinear?
3. What point belongs to neither Plane V nor Plane \(W\)?
4. List three points in Plane \(W\).

Solution

1. Neither
2. Yes
3. S
4. Any combination of \(P\), \(O\), \(T\), and \(Q\) would work.

Example \(\PageIndex{5}\)

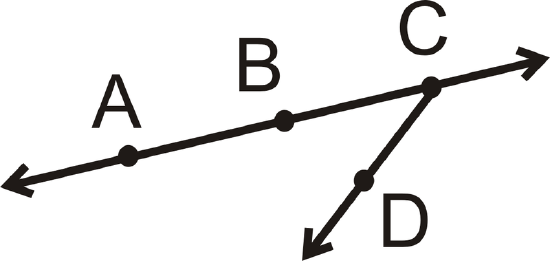
Draw and label a figure matching the following description: Line \(\overleftrightarrow{AB}\) and ray \(\overrightarrow{CD}\) intersect at point \(C)\. Then, redraw so that the figure looks different but is still true to the description.

Solution

Neither the position of A or B on the line, nor the direction that \(\overrightarrow{CD}\) points matter.

Figure \(\PageIndex{16}\)

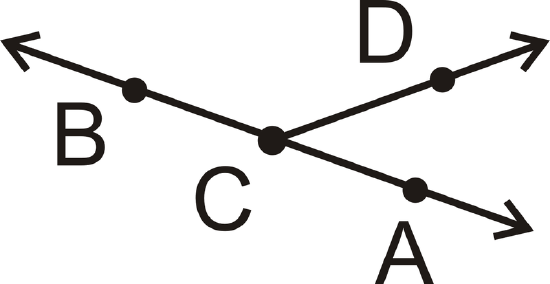
For the second part, this is one way to draw the diagram differently:

Figure \(\PageIndex{17}\)

Review

For questions 1-5, draw and label a figure to fit the descriptions.

1. \(\overrightarrow{CD}\) intersecting \(\overline{AB}\) and Plane \(P\) containing \(\overline{AB}\) but not \(\overrightarrow{CD}\).
2. Three collinear points \(A\), \(B\), and \(C\). \(B\) is also collinear with points \(D\) and \(E\).
3. \(\overrightarrow{XY}\), \(\overrightarrow{XZ}\), and \(\overrightarrow{XW}\), such that \(\overrightarrow{XY}\) and \(\overrightarrow{XZ}\) are coplanar, but \(\overrightarrow{XW}\) is non-coplanar with both of the other rays.
4. Two intersecting planes, \(P\) and \(Q\), with \(\overline{GH}\), where \(G\) is in plane \(P\) and \(H\) is in plane \(Q\).
5. Four non-collinear points \(I\), \(J\), \(K\),and \(L\), with line segments connecting all points to each other.
6. Name this line in five ways.

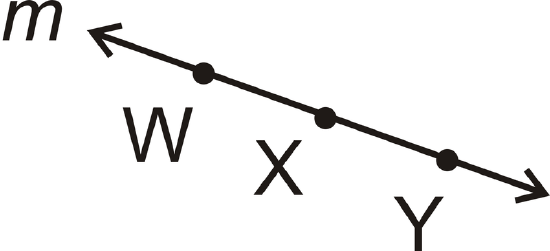
Figure \(\PageIndex{18}\)

7. Name the geometric figure in three different ways.

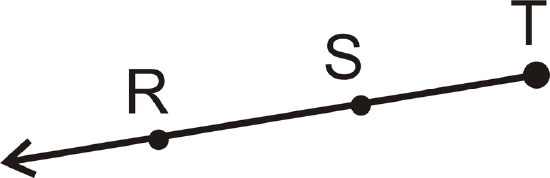
Figure \(\PageIndex{19}\)

8. Name the geometric figure in two different ways.

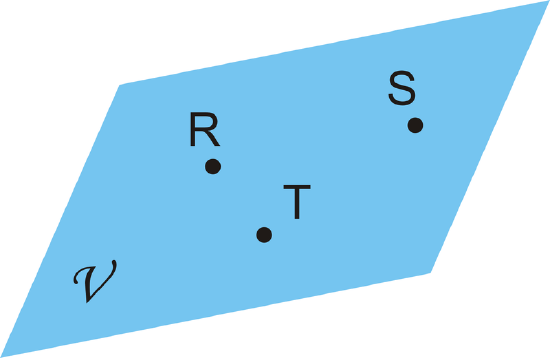
Figure \(\PageIndex{20}\)

9. What is the best possible geometric model for a soccer field? Explain your answer.
10. List two examples of where you see rays in real life.
11. What type of geometric object is the intersection of a line and a plane? Draw your answer.
12. What is the difference between a postulate and a theorem?

For 13-16, use geometric notation to explain each picture in as much detail as possible.

13. 

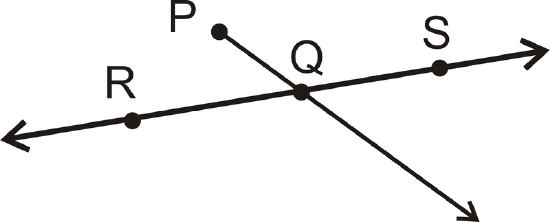
    Figure \(\PageIndex{21}\)

14. 

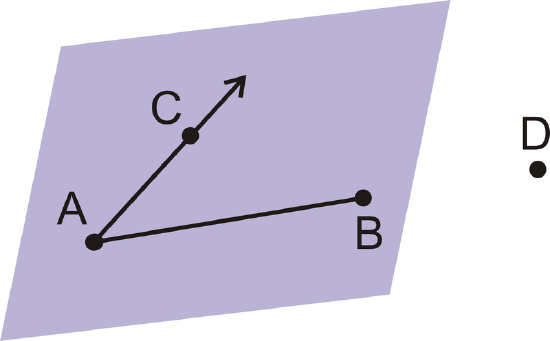
    Figure \(\PageIndex{22}\)

15. 

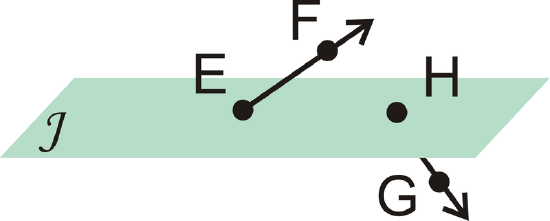
    Figure \(\PageIndex{23}\)

16. 

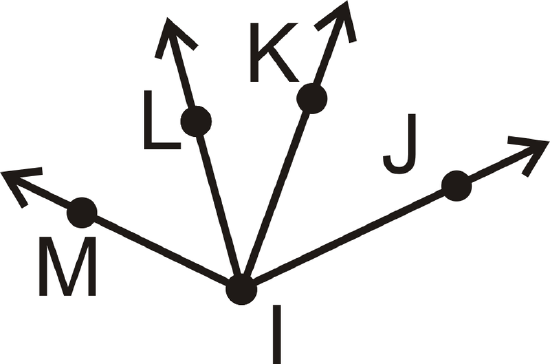
    Figure \(\PageIndex{24}\)

For 17-25, determine if the following statements are true or false.

17. Any two points are collinear.
18. Any three points determine a plane.
19. A line is two rays with a common endpoint.
20. A line segment is infinitely many points between two endpoints.
21. A point takes up space.
22. A line is one-dimensional.
23. Any four points are coplanar.
24. \(\overrightarrow{AB}\) could be read “ray \(AB\)” or “ray \(BA\).”
25. \(\overleftrightarrow{AB}\) could be read “line \(AB\)” or “line \(BA\).”

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.1.

Vocabulary

Term	Definition
collinear	Three or more points are collinear when they lie on the same line.
coplanar	Points and/or lines located on the same plane are coplanar.
endpoint	An endpoint is a point at one end of a line segment or ray.
intersection	A point or set of points where lines, planes, segments, or rays cross.
line	Infinitely many points that extend forever in both directions.
line segment	A line segment is a part of a line that has two endpoints.
plane	A plane is a flat, two-dimensional surface. It can be conceptualized as a sheet of paper of infinite area.
Point	A point is a location in space that does not have size or shape.
postulate	A postulate is a statement that is accepted as true without proof.
ray	A part of a line with one endpoint that extends forever in the direction opposite that point.
space	Space is the set of all points extending in three dimensions.
Dimensions	Dimensions are the measurements that define the shape and size of a figure.
Non-collinear	A non-collinear point is located above or below a line.
Non-coplanar	A non-coplanar point is located above or below a plane.
theorem	A theorem is a statement that can be proven true using postulates, definitions, and other theorems that have already been proven.

Additional Resources

Interactive Element

Video: Basic Geometric Definitions Principles - Basic

Activities: Basic Geometric Definitions Discussion Questions

Study Aids: Basics of Geometry Study Guide

Practice: Geometry Terms

Real World: Basic Geometric Definitions