1.10: Classifying Angles
- Page ID
- 2121
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angle Classification
Figure \(\PageIndex{1}\)Mark wants to paint his bedroom door. The shapes on the door remind him of geometry. He decides to use a ruler to measure the actual lengths of the sides and a protractor to measure the angles. He notices the same angle repeating over and over again. What type of angle is formed by the corner of the door?
In this concept, you will learn how to classify angles.
Classifying Angles
An angle is the space created between two lines, line segments or rays connected at a common point.
Angles can be represented by using a symbol. Here is the symbol for an angle.
\(\angle A\)
This means “Angle A”.
Angles are measured in degrees. Degrees measure the distance between the two lines. The o symbol means “degrees.” The number of degrees tells how open or closed the angle is. The smaller the number of degrees, the smaller or more closed the angle.
Angles are classified by their size. Angle sizes can range from \(0^{\circ}\) to \(360^{\circ}\), a complete circle.
Here is a diagram that shows some angle measurements.
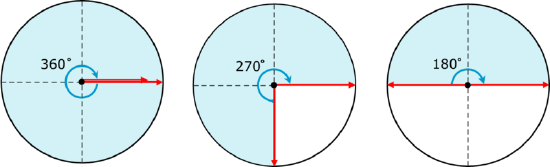Figure \(\PageIndex{2}\)As you can see, an angle of \(360^{\circ}\) makes a complete circle. An angle of \(270^{\circ}\) is three-quarters of a circle, and an angle of \(180^{\circ}\) is half a circle. A \(180^{\circ}\) angle is a straight line.
Angles that measure between 0o and \(180^{\circ}\) are classified as acute, right, obtuse, or straight.
An acute angle measures less than \(90^{\circ}\).
An obtuse angle has a measure greater than \(90^{\circ}\) and less than \(180^{\circ}\).
Here are a few examples.
Figure \(\PageIndex{3}\)Most angles in the \(0^{\circ}\) and \(180^{\circ}\) range are either acute or obtuse. However, there are two special angles with exact measurements.
A right angle measures exactly \(90^{\circ}\). Right angles are one of the most important concepts you need to know about geometry. Right angles are found in squares, rectangles, and triangles. They are everywhere in the real world too.
Here are a few examples.
Figure \(\PageIndex{4}\)Notice that a small box is used when an angle is a right angle.
There are many places in the real world where you can see acute, obtuse and right angles.
Here are a few examples.
Figure \(\PageIndex{5}\)If you look at each of these pictures, you can see the right angles clearly. Also notice that the wires of the bridge stretch to create acute angles on each side of the center beam.
The other special angle is called a straight angle. A straight angle forms a line and measures exactly 180∘.
Let's look at an example.
Figure \(\PageIndex{6}\)Now, let’s try classifying angles.
Classify each angle below.
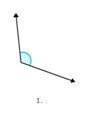Figure \(\PageIndex{7}\)For each angle, it may help to ask yourself: “Is it bigger or smaller than a right angle?”
Remember, right angles always measure \(90^{\circ}\), and are used to tell whether an angle is acute or obtuse.
First, understand that the angle in Figure \(\PageIndex{2}\) is not a right angle or straight angle.
The angle does not have a perfect corner to represent a right angle and the angle is not a straight line.
Next, determine if the angle in Figure \(\PageIndex{2}\) is larger or smaller than a right angle.
The angle is larger than a perfect corner, therefore, the angle is larger than a right angle.
Then, classify the angle.
Obtuse.
The answer is that Figure \(\PageIndex{2}\) shows an obtuse angle.
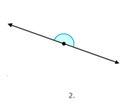Figure \(\PageIndex{8}\)The angle in Figure \(\PageIndex{3}\) appears to be a straight line.
First, recognize that Figure \(\PageIndex{3}\) appears to be a straight line.
The line does not appear to bend.
Next, remember the meaning of a straight line.
A straight line is a special angle.
Then, classify the angle.
Straight.
The answer is that Figure \(\PageIndex{3}\) shows a straight angle.
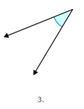Figure \(\PageIndex{9}\)Is Figure \(\PageIndex{4}\) larger or smaller than a right angle?
First, understand that the angle in Figure \(\PageIndex{4}\) is not a right angle or straight angle.
The angle does not have a perfect corner to represent a right angle and the angle is not a straight line.
Next, determine if the angle in Figure \(\PageIndex{4}\) is larger or smaller than a right angle.
The angle is smaller than a right angle.
Then, classify the angle.
Acute.
The answer is that Figure \(\PageIndex{4}\) shows an acute angle.
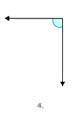Figure \(\PageIndex{10}\)The angle in Figure \(\PageIndex{5}\) appears to be a special type of angle.
First, recognize the appearance of the angle in Figure \(\PageIndex{5}\).
The angle appears to form a perfect corner.
Next, remember what a perfect corner represents.
A perfect corner represents a special angle.
Then, classify the angle.
Right.
The answer is that Figure \(\PageIndex{5}\) shows a right angle.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Mark and his bedroom door.
He notices the same angle on multiple different places on the door. What type of angle is formed by the corner of the door?
Solution
First, highlight the relevant angles.
Highlight each corner angle.
Next, list the angle options.
Acute, right, obtuse.
Then, label the corner angle.
Right.
The answer is that the corners of the door are right angles.
Example \(\PageIndex{2}\)
True or false. An acute angle can also be a right angle.
Solution
First, recall the definition of an acute angle.
An acute angle is less than \(90^{\circ}\).
Next, remember that angles measuring exactly \(90^{\circ}\) are special angles.
Angles measuring exactly \(90^{\circ}\) are classified as right angles.
Then, state your conclusion.
An acute angle cannot be a right angle.
The answer is that the statement is false. An acute angle measures less than \(90^{\circ}\) while a right angle measures exactly \(90^{\circ}\), therefore, an acute angle cannot be a right angle.
Example \(\PageIndex{3}\)
Identify each type of angle described.
An angle greater than \(90^{\circ}\) but less than \(180^{\circ}\).
Solution
First, note the size of the angle.
The angle is greater than \(90^{\circ}\) but less than \(180^{\circ}\).
Next, remember the rules for angles.
There is a name for angles greater than \(90^{\circ}\) but less than \(180^{\circ}\).
Then, classify the angle.
Obtuse.
The answer is that the angle is obtuse.
Example \(\PageIndex{4}\)
Identify each type of angle described.
An angle that measures \(15^{\circ}\).
Solution
First, note the size of the angle.
The angle is less than \(90^{\circ}\).
Next, remember the rules for angles.
There is a name for angles that are less than \(90^{\circ}\).
Then, classify the angle.
Acute.
The answer is that the angle is acute.
Example \(\PageIndex{5}\)
Identify each type of angle described.
An angle that measures exactly \(90^{\circ}\)
Solution
First, note the size of the angle.
The angle is exactly \(90^{\circ}\).
Next, remember the rules for angles.
There is a name for angles that are exactly \(90^{\circ}\).
Then classify the angle.
Right.
The answer is that the angle is a right angle.
Review
Label each angle as acute, obtuse, right, or straight.
Figure \(\PageIndex{11}\)- \(55^{\circ}\)
- \(102^{\circ}\)
- \(90^{\circ}\)
- \(180^{\circ}\)
- \(10^{\circ}\)
- \(87^{\circ}\)
- \(134^{\circ}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.1.
Resources
Additional Resource
Interactive Element
Video:Animation of Types of Angles
Activities: Angle Classification Discussion Questions
Study Aids: Angles Study Guide
Practice: Classifying Angles
Real Worlds: Angle Classification