1.11: Congruent Angles and Angle Bisectors
- Page ID
- 2124
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles of the same measure, and lines or portions of lines that divide angles into two equal halves.
When two geometric figures have the same shape and size (or the same angle measure in the case of angles) they are said to be congruent.
| Label It | Say It |
|---|---|
| \(\angle ABC \cong \angle DEF\) | Angle \(ABC\) is congruent to angle \(DEF\). |
If two angles are congruent, then they are also equal. To label equal angles we use angle markings, as shown below:
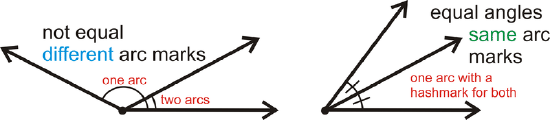Figure \(\PageIndex{1}\)An angle bisector is a line, or a portion of a line, that divides an angle into two congruent angles, each having a measure exactly half of the original angle. Every angle has exactly one angle bisector.
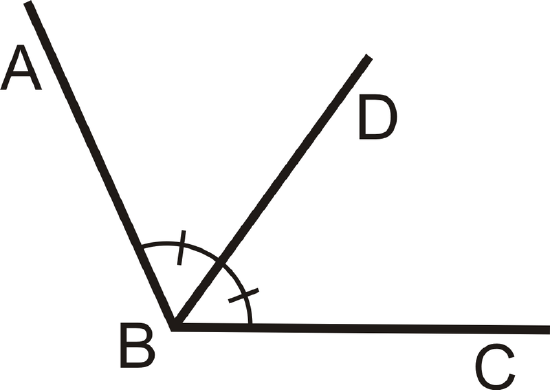Figure \(\PageIndex{2}\)In the picture above, \(\overline{BD}\) is the angle bisector of \(\angle ABC\), so \(\angle ABC \cong \angle DBC\) and \(m \angle ABD \cong \dfrac{1}{2} m \angle ABC\).
What if you were told that a line segment divides an angle in half? How would you find the measures of the two new angles formed by that segment?
For Examples 1 and 2, copy the figure below and label it with the following information:
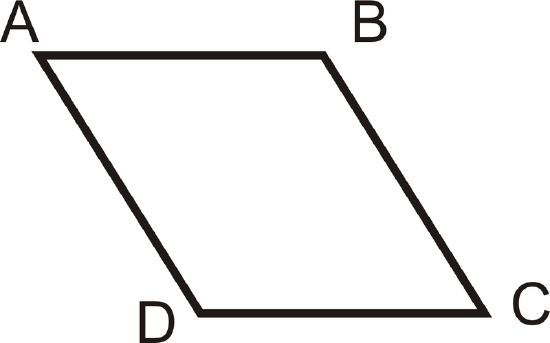Figure \(\PageIndex{3}\)Example \(\PageIndex{1}\)
\(\angle A \cong \angle C\)
Solution
You should have corresponding markings on \(\angle A\) and \(\angle C\).
Example \(\PageIndex{2}\)
\(\angle B \cong \angle D\)
Solution
You should have corresponding markings on \(\angle B\) and \(\angle D\) (that look different from the markings you made in Example 1).
Example \(\PageIndex{3}\)
Write all equal angle statements.
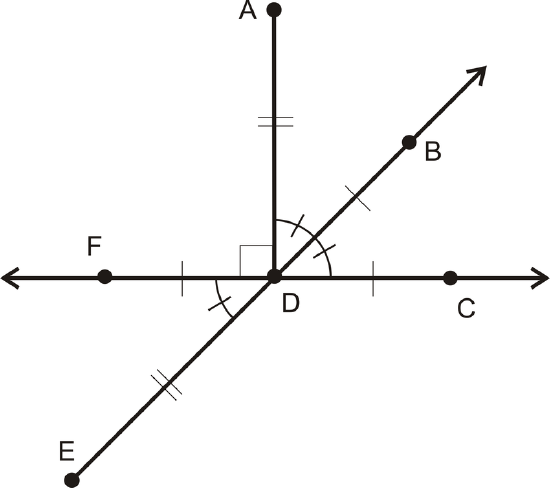Figure \(\PageIndex{4}\)Solution
\(m \angle ADB=m\angle BDC=m \angle FDE=45^{\circ}\)
\(m \angle ADF=m\angle ADC=90^{\circ}\)
Example \(\PageIndex{4}\)
What is the measure of each angle?
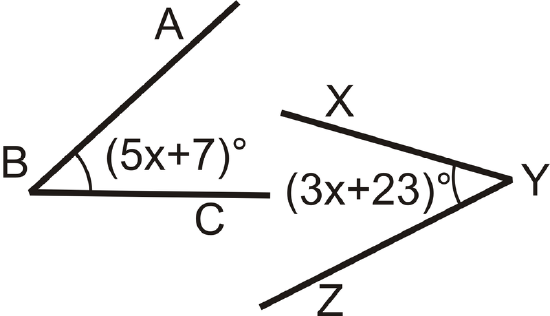Figure \(\PageIndex{5}\)Solution
From the picture, we see that the angles are equal.
Set the angles equal to each other and solve.
\((5x+7)^{\circ} = (3x+23)^{\circ}\)
\((2x)^{\circ}= 16^{\circ}\)
\(x=8\)
To find the measure of \(\angle ABC\), plug in \(x=8\) to
\((5x+7)^{\circ} \rightarrow (5(8)+7)^{\circ} =(40+7)^{\circ}=47^{\circ}\).
Because \(m \angle ABC=m \angle XYZ\), \(m \angle XYZ=47^{\circ}\) too.
Example \(\PageIndex{5}\)
Is \(\overline{OP}\) the angle bisector of \(\angle SOT\)?
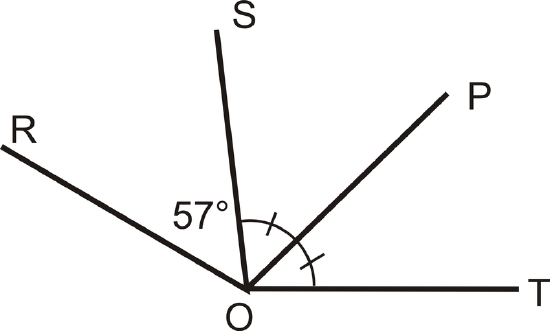Figure \(\PageIndex{6}\)Solution
Yes, \(\overline{OP}\) is the angle bisector of \(\angle SOT\) from the markings in the picture.
Review
For 1-4, use the following picture to answer the questions.
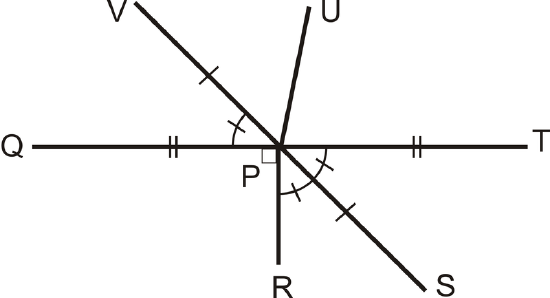Figure \(\PageIndex{7}\)- What is the angle bisector of \(\angle TPR\)?
- What is \(m \angle QPR\)?
- What is \(m \angle TPS\)?
- What is \(m \angle QPV\)?
For 5-6, use algebra to determine the value of variable in each problem.
-
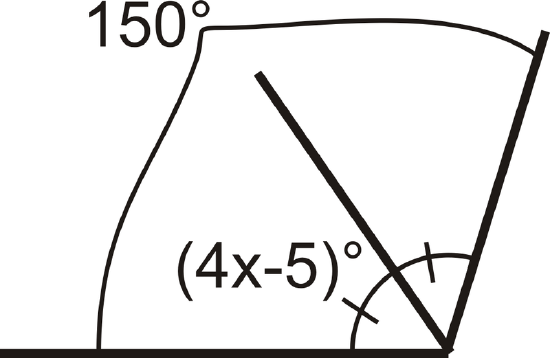Figure \(\PageIndex{8}\) -
Figure \(\PageIndex{9}\)
For 7-10, decide if the statement is true or false.
- Every angle has exactly one angle bisector.
- Any marking on an angle means that the angle is \(90^{\circ}\).
- An angle bisector divides an angle into three congruent angles.
- Congruent angles have the same measure.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.3.
Vocabulary
| Term | Definition |
|---|---|
| angle bisector | An angle bisector is a ray that splits an angle into two congruent, smaller angles. |
| Congruent | Congruent figures are identical in size, shape and measure. |
Additional Resource
Interactive Element
Video: Congruent Angles and Angle Bisectors Principles - Basic
Activities: Congruent Angles and Angle Bisectors Discussion Questions
Study Aids: Angles Study Guide
Practice: Congruent Angles and Angle Bisectors
Real World: Starry Night