1.12: Constructions and Bisectors
- Page ID
- 2125
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Construct angles and line segments. Divide angles and line segments into two congruent parts.
Bisectors of Line Segments and Angles
Describe how to construct a \(45^{\circ}\) angle using a compass and a straightedge.
Bisectors
A construction is similar to a drawing in that it produces a visual outcome. However, while drawings are often just rough sketches that help to convey an idea, constructions are step-by-step processes used to create accurate geometric figures. To create a construction by hand, there are a few tools that you can use:
- Compass: A device that allows you to create a circle with a given radius. Not only can compasses help you to create circles, but also they can help you to copy distances.
- Straightedge: Anything that allows you to produce a straight line. A straightedge should not be able to measure distances. An index card works well as a straightedge. You can also use a ruler as a straightedge, as long as you only use it to draw straight lines and not to measure.
- Paper: When a geometric figure is on a piece of paper, the paper itself can be folded in order to construct new lines.
To bisect a segment or an angle means to divide it into two congruent parts. A bisector of a line segment will pass through the midpoint of the line segment. A perpendicular bisector of a segment passes through the midpoint of the line segment and is perpendicular to the line segment. In order to construct bisectors of segments and angles, it's helpful to remember some relevant theorems:
Any point on the perpendicular bisector of a line segment will be equidistant from the endpoints of the line segment. This means that one way to find the perpendicular bisector of a segment (such as \(\overline{AB}\)below) is to find two points that are equidistant from the endpoints of the line segment (such as C and D below) and connect them.
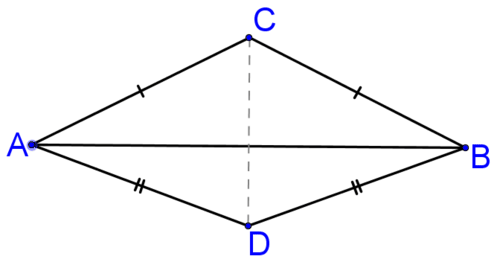Figure \(\PageIndex{1}\)Any point on the angle bisector of an angle will be equidistant from the rays that create the angle. This means that one way to find the angle bisector of an angle (such as \(\angle BAC\) below) is to find two points that are equidistant from the rays that create the angle (such as points A and D below).
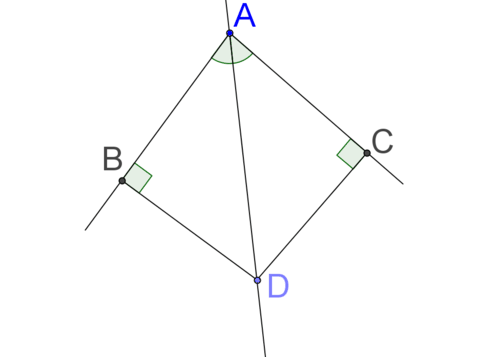Figure \(\PageIndex{2}\)Let's take a look at different ways to find the perpendicular bisector of a line segment.
1. Draw a line segment like the orange one below on a piece of paper (the rectangle below represents the paper). Fold the paper in order to find the perpendicular bisector of the line segment.
Figure \(\PageIndex{3}\)To find the perpendicular bisector, fold the paper so that the endpoints lie on top of each other. By doing this, you have matched the two halves of the line segment exactly.
Any point on the fold is now equidistant from both endpoints, because the endpoints are now in the same place! This means that the crease made by the fold will be the perpendicular bisector of the line segment.
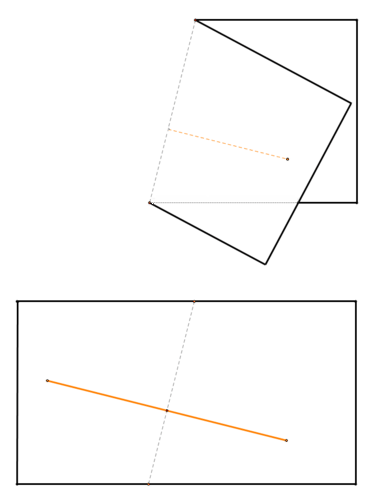Figure \(\PageIndex{4}\)2. Draw a line segment like the orange one below on a piece of paper (the rectangle below represents the paper). Use a compass and straightedge to find the perpendicular bisector of the line segment.
Figure \(\PageIndex{5}\)Use your compass to draw a circle centered at each endpoint with the same radius. Make sure the radius of the circles is large enough so that the circles will intersect. If the circles are too big to fit on the paper, draw the portion of the circle that fits on the paper. Here is the first circle:
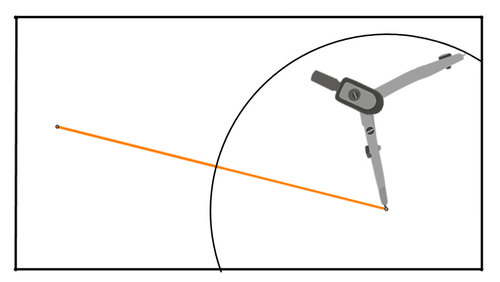Figure \(\PageIndex{6}\)Here is the second circle:
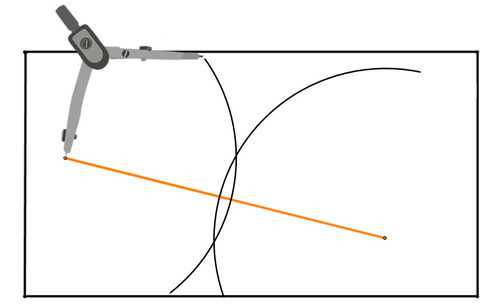Figure \(\PageIndex{7}\)The points of interest are the two points where the circles intersect. Because the radius of each circle is the same, each of these points are equidistant from the endpoints of the line segment.
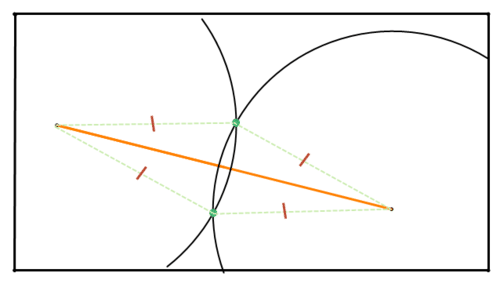Figure \(\PageIndex{8}\)Therefore, each of these points lies on the perpendicular bisector of the line segment. Use your straightedge to draw a line connecting the two intersection points. This is the perpendicular bisector of the line segment.
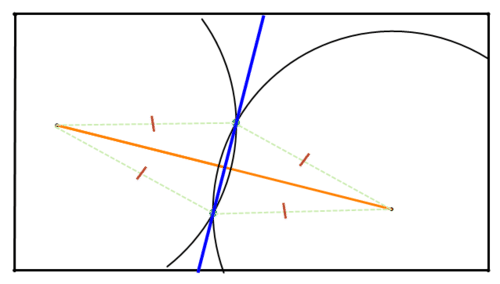Figure \(\PageIndex{9}\)How can you use a compass and straightedge to find the midpoint of a line segment?
One way is to use the process from Example B to construct the perpendicular bisector. The midpoint of the line segment will be the point where the perpendicular bisector intersects the line segment.
Example \(\PageIndex{1}\)
Earlier, you were asked how to construct a \(45^{\circ}\) angle using a compass and a straightedge.
One way to construct a \(45^{\circ}\) angle is to:
- Draw a segment and construct its perpendicular bisector. This will give you \(90^{\circ}\) angles.
- Construct the angle bisector of one of those \(90^{\circ}\) angles. This will produce two \(45^{\circ}\) angles. Note: Steps for constructing an angle bisector are explored in the guided practice questions.
Can you think of another way to construct a perfect \(45^{\circ}\) angle with just a compass and a straightedge?
Example \(\PageIndex{2}\)
Draw an angle like the one below on a piece of paper (the rectangle below represents the paper). Note that the two segments creating the angle do NOT need to be the same length. Fold the paper to create the bisector of the angle.
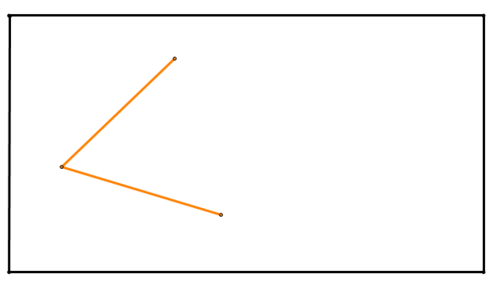Figure \(\PageIndex{10}\)Solution
Fold the paper so that one segment overlaps the other segment. The crease will be the angle bisector.
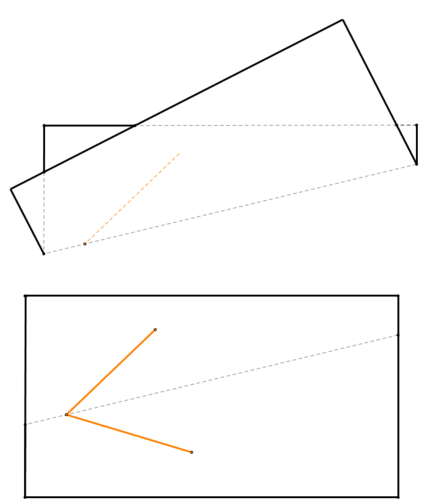Figure \(\PageIndex{11}\)Example \(\PageIndex{3}\)
Draw an angle like the one below on a piece of paper (the rectangle below represents the paper). Note that the two segments creating the angle do NOT need to be the same length. Use a compass and straightedge to find the bisector of the angle.
Figure \(\PageIndex{12}\)Solution
Use your compass to create a portion of a circle centered at the vertex of the angle that passes through both segments creating the angle:
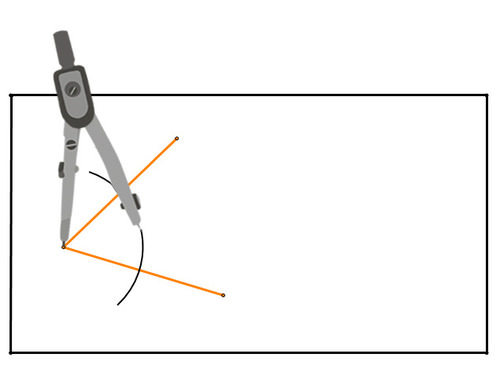Figure \(\PageIndex{13}\)
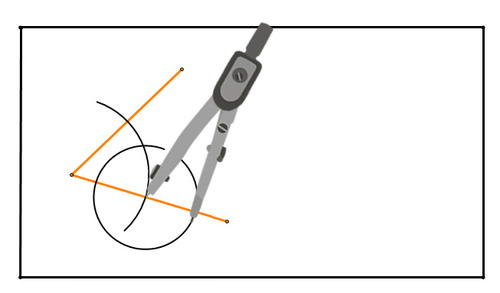Figure \(\PageIndex{14}\)Here is the second circle:
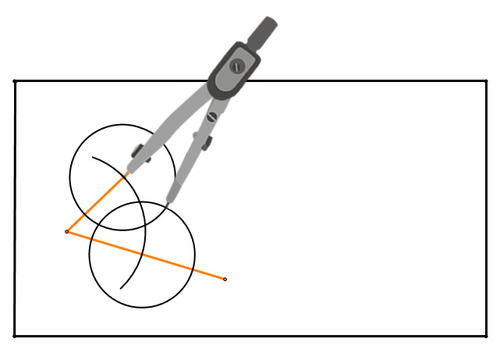Figure \(\PageIndex{15}\)The points where the circles intersect are equidistant from the segments creating the angle. Therefore, they define the bisector of the angle. Connect those intersection points to create the angle bisector:
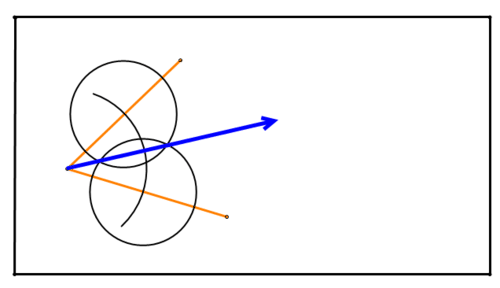Figure \(\PageIndex{16}\)Example \(\PageIndex{4}\)
Prove that the angle bisector created using the method in #2 is actually the angle bisector.
Consider the construction from #2 below. Points have been labeled and two additional segments have been drawn in (shown in green):
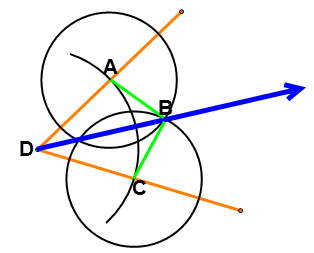Figure \(\PageIndex{17}\)Solution
In this picture, \(\oveline{AD} \cong \overline{CD}\)because they are both radiuses of the same partial circle centered at point \(D\). \(\overline{AB} \cong \oveline{CB}\) because they are both radiuses of congruent circles centered at \(A\) and \(C\) respectively. \(\overline{BD} \cong \overline{BD}\) by the reflexive property. Therefore, \(\Delta ABD \cong \Delta CBD\) by \(SSS \cong\). \(\angle ADB \cong \angle BDC\) because they are corresponding parts of congruent triangles. Therefore, \(\overrightarrow{BD}\) must be the angle bisector of \(\angle ADC\).
Review
- What does it mean to bisect a segment or an angle?
- Describe the steps for finding the perpendicular bisector of a line segment.
- Describe how to use the perpendicular bisector of a line segment to find the midpoint of the line segment.
- What's the difference between a bisector and a perpendicular bisector? How can you construct a non-perpendicular bisector of a line segment?
- Draw a line segment on your paper and construct the perpendicular bisector of the segment.
- Draw another line segment on your paper and construct the perpendicular bisector of that segment using another method.
- Draw an angle on your paper and construct the bisector of the angle.
- Draw another angle on your paper and construct the bisector of that angle using another method.
- Use your straightedge to draw a triangle on your paper. Construct the angle bisector of each angle. What point have you found?
- Use your straightedge to draw a triangle on your paper. Construct the perpendicular bisector of each side of the triangle. What point have you found?
- Use the triangle and your work from #10. Construct the medians of the triangle. What point have you found?
- Compare and contrast the two methods for finding a bisector-paper folding vs. compass and straightedge.
- Construct a \(45^{\circ}\) angle (look at the concept problem for help). Then, construct a \(22.5^{\circ}\) angle.
- Construct an isosceles right triangle. Hint: Start by creating a right angle by constructing a perpendicular bisector.
- If possible, extend your construction of an isosceles right triangle to construct a square. Describe your steps.
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.2.
Vocabulary
| Term | Definition |
|---|---|
| perpendicular bisector | A perpendicular bisector of a line segment passes through the midpoint of the line segment and intersects the line segment at \(90^{\circ}\). |
| Ray | A ray is a part of a line that has one endpoint and continues indefinitely in one direction. |
| Bisector | A bisector divides a line segment or angle into two congruent parts. |
Additional Resource
Interactive Element