1.13: Angle Properties and Theorems
- Page ID
- 2126
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find angles and line segments, and determine if shapes are congruent and lines are parallel. Understand complementary angles as angles whose sum is 90 degrees and supplementary angles as angles whose sum is 180 degrees.
Measures of Angle Pairs
Figure \(\PageIndex{1}\)The foul lines of a baseball diamond intersect at home plate to form a right angle. A baseball is hit from home plate and forms an angle of \(36^{\circ}\) with the third base foul line. What is the measure of the angle between the first base foul line and the bath of the baseball?
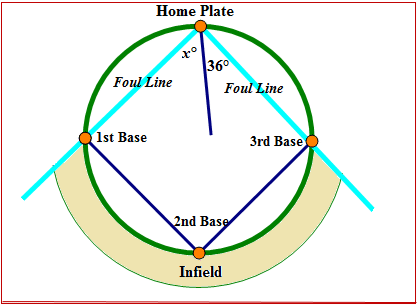Figure \(\PageIndex{2}\)How can you use your knowledge of angles to figure out the measure of the angle?
In this concept, you will learn measure of angle pairs.
Measuring Angle Pairs
There are different types of angle pairs. Vertical angles are an angle pair formed by intersecting lines such that they are never adjacent. They have a common vertex and never share a common side. Vertical angles are equal in measure. The following diagram shows vertical angle pairs.
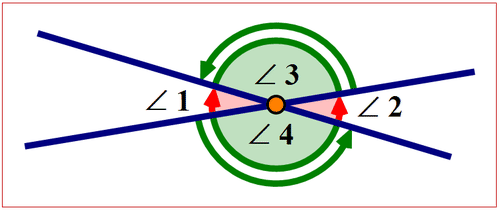Figure \(\PageIndex{3}\)\(\angle 1\) and \(\angle 2\) are vertical angles. \(m\angle 1=m\angle 2\)
\(\angle 3\) and \(\angle 4\) are vertical angles. \(m\angle 3=m\angle 4\)
Adjacent angles are an angle pair also formed by two intersecting lines. Adjacent angles are side by side, have a common vertex and share a common side. The following diagram shows pairs of adjacent angles.
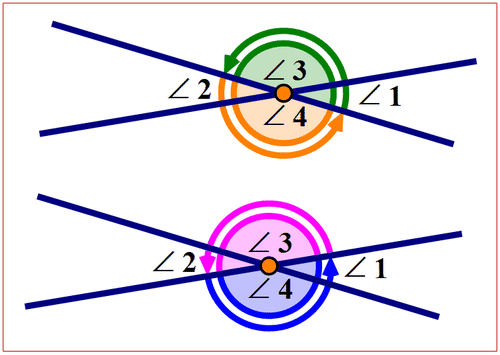Figure \(\PageIndex{4}\)Each pair of adjacent angles forms a straight angle. Therefore the sum of any two adjacent angles equals \(180^{\circ}\).
\(m\angle 1+m \angle 3= 180^{\circ}\)
\(m\angle 2+m \angle 4= 180^{\circ}\)
\(m\angle 2+m \angle 3= 180^{\circ}\)
\(m\angle 1+m \angle 4= 180^{\circ}\)
If the sum two angles is \(180^{\circ}\) then the angles are called supplementary angles. The following diagram shows two supplementary angles.
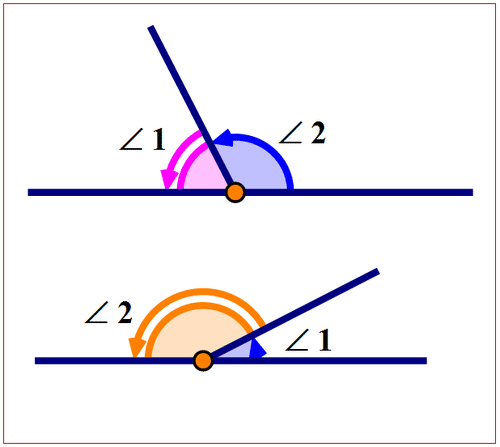Figure \(\PageIndex{5}\)In both diagrams, \(m\angle 1+m \angle 2= 180^{\circ}\).
If the sum of two angles equals 90° then the angles are called complementary angles. The following diagram shows two complementary angles.
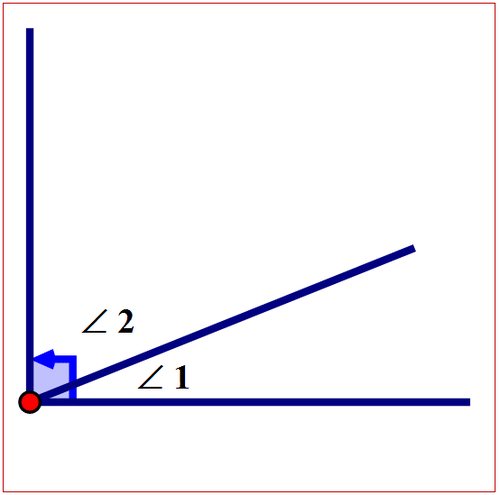Figure \(\PageIndex{6}\)\(m\angle 1+m \angle 2= 90^{\circ}\)
Let’s apply all this information about angles and their measure to determine the measure of \(\angle a\), \(\angle b\), \(\angle c\) in the following diagram.
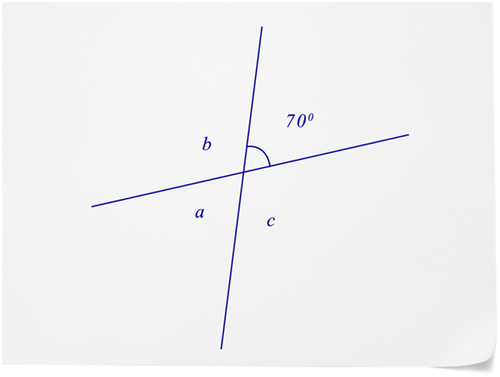Figure \(\PageIndex{7}\)There are four angles formed by intersecting lines. The measure of one of the angles is \(70^{\circ}\).
First, state the relationship between the angle of \(70^{\circ}\) and \(\angle b\).
The angle of \(70^{\circ}\). is adjacent to \(\angle b\) and the two angles form a straight angle.
Next, express the relationship using symbols.
\(\angle b+70^{\circ}=180^{\circ}\)
Next, subtract 70° from both sides of the equation.
\(\angle b+70^{\circ}=180^{\circ}\)
\(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)
Then, simplify both sides of the equation.
\(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)
\(\angle b = 110^{\circ}\)
The answer is \(110^{\circ}\).
\(m \angle b = 110^{\circ}\)
First, state the relationship between the angle of \(70^{\circ}\) and \(\angle a\).
The angle of \(70^{\circ}\) and \(\angle a\) are vertical angles and are equal in measure.
Next, express the relationship using symbols.
\(m\angle a=70^{\circ}\)
The answer is \(70^{\circ}\).
\(m\angle a=70^{\circ}\)
First state the relationship between the angle of \(70^{\circ}\) and \(\angle c\).
The angle of \(70^{\circ}\) is adjacent to \(\angle c\) and the two angles form a straight angle.
Next, express the relationship using symbols.
\(\angle c+70^{\circ}=180^{\circ}\)
Next, subtract \(70^{\circ}\) from both sides of the equation.
\(\angle c+70^{\circ}=180^{\circ}\)
\(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)
Then, simplify both sides of the equation.
\(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)
\(\angle c=110^{\circ}\)
The answer is \(110^{\circ}\).
\(m \angle c=110^{\circ}\)
Example \(\PageIndex{1}\)
Earlier, you were given a problem about the baseball field and the foul lines.
The angle between the path of the ball and the first base foul line needs to be figured out. This can be done using complementary angles.
Solution
First, draw a diagram to model the problem.
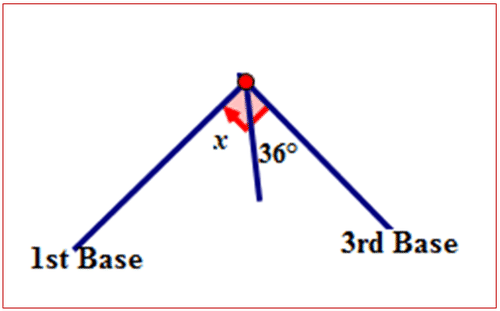Figure \(\PageIndex{8}\)Next, state the relationship between \(36^{\circ}\) and \(\angle x\).
\(36^{\circ}\) and \(\angle x\) are complementary angles. The sum of the angles is \(90^{\circ}\).
Next, express the relationship using symbols.
\(36^{\circ}+\angle x=90^{\circ}\)
Next, subtract 36° from both sides of the equation.
\(36^{\circ}+\angle x=90^{\circ}\)
\(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)
Then, simplify both sides of the equation.
\(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)
\(\angle x = 54^{\circ}\)
The answer is \(54^{\circ}\).
An angle of \(54^{\circ}\) is made between the first base foul line and the path of the baseball.
Example \(\PageIndex{2}\)
If the following angles are complementary, find the measure of the missing angle.
\(\angle A=37^{\circ}\) then \(\angle B=\)?
Solution
First, draw a diagram to model the problem.
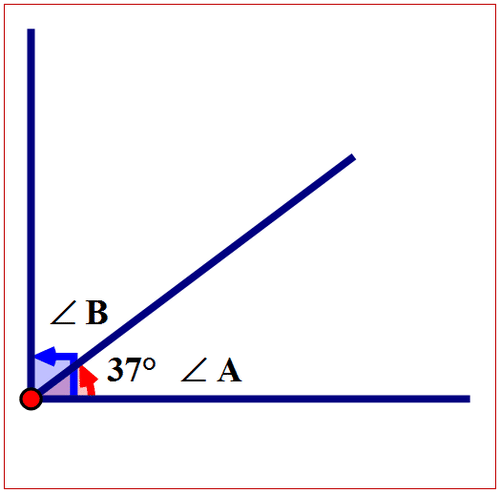Figure \(\PageIndex{9}\)Next, state the relationship between \(\angle A\) and \(\angle B\).
\(\angle A\) and \(\angle B\) are complementary angles. The sum of the angles is \(90^{\circ}\).
Next, express the relationship using symbols.
\(\angle A+ \angle B=90^{\circ}\)
Next, substitute the measure of \(\angle A\) into the equation.
\(37^{\circ}+ \angle B=90^{\circ}\)
Next, subtract \(37^{\circ}\) from both sides of the equation.
\(37^{\circ}+ \angle B=90^{\circ}\)
\(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)
Then, simplify both sides of the equation.
\(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)
\(\angle B =53^{\circ}\)
The answer is \(53^{\circ}\).
\(m \angle B =53^{\circ}\)
Example \(\PageIndex{3}\)
If the following angles are supplementary, find the measure of the missing angle.
\(\angle A=102^{\circ}\) then \(\angle B=\)?
Solution
First, draw a diagram to model the problem.
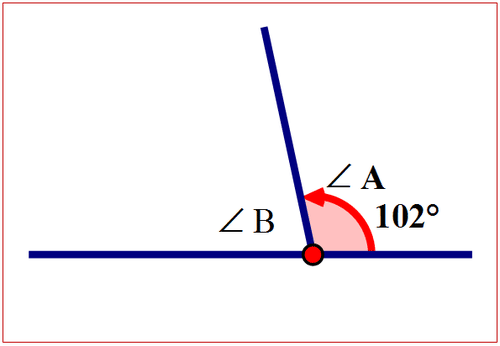Figure \(\PageIndex{10}\)Next, state the relationship between \(\angle A\) and \(\angle B\).
\(\angle A\) and \(\angle B\) are supplementary angles. The sum of the angles is 180°.
Next, express the relationship using symbols.
\(\angle A+ \angle B=180^{\circ}\)
Next, substitute the measure of \(\angle A\) into the equation.
\(102^{\circ}+\angle B=180^{\circ}\)
Next, subtract \(102^{\circ}\) from both sides of the equation.
\(102^{\circ}+\angle B=180^{\circ}\)
\(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)
Then, simplify both sides of the equation.
\(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)
\(\angle B=78^{\circ}\)
The answer is \(78^{\circ}\).
\(m \angle B=78^{\circ}\)
Example \(\PageIndex{4}\)
Using the following diagram, determine the measures of the missing angles.
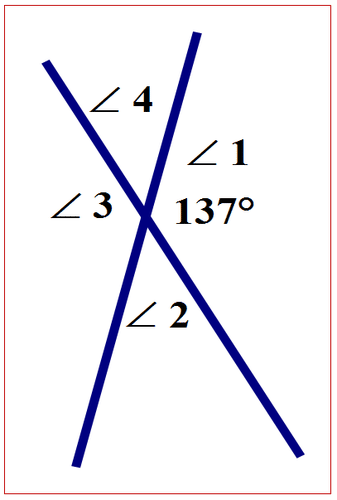Figure \(\PageIndex{11}\)Solution
First, state the relationship between the angle of \(\angle 1\) and \(\angle 3\).
\(\angle 1\) and \(\angle 3\) are vertical angles and are equal in measure.
Next, express the relationship using symbols.
\(m\angle 1=m \angle 3\)
Next, substitute the measure of \(\angle 1\) into the equation.
\(m\angle 1=m \angle 3\)
\(137^{\circ}=m\angle 3\)
The answer is \(137^{\circ}\).
\(m\angle 3= 137^{\circ}\)
First, state the relationship between the angle of \(\angle 1\) and \(\angle 2\).
\(\angle 1\) is adjacent to \(\angle 2\) and the two angles form a straight angle.
Next, express the relationship using symbols.
\(\angle 1+\angle 2=180^{\circ}\)
Next, substitute the measure of \(\angle 1\) into the equation.
\(137^{\circ}+\angle 2=180^{\circ}\)
Next, subtract \(137^{\circ}\) from both sides of the equation.
\(137^{\circ}+\angle 2=180^{\circ}\)
\(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)
Then, simplify both sides of the equation.
\(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)
\(\angle 2=43^{\circ}\)
The answer is \(43^{\circ}\).
\(m \angle 2=43^{\circ}\)
First, state the relationship between the angle of \(\angle 2\) and \(\angle 4\).
\(\angle 2\) and \(\angle 4\) are vertical angles and are equal in measure.
Next, express the relationship using symbols.
\(m \angle 2=m \angle 4\)
Next, substitute the measure of \(\angle 2\) into the equation.
\(m \angle 2=m \angle 4\)
\(43^{\circ}=m \angle 4\)
The answer is \(43^{\circ}\).
\(m \angle 4=43^{\circ}\)
Review
If the following angle pairs are complementary, then what is the measure of the missing angle?
1. If \(\angle A=45^{\circ}\) then \(\angle B=\)?
2. If \(\angle C=83^{\circ}\) then \(\angle D=\)?
3. If \(\angle E=33^{\circ}\) then \(\angle F=\)?
4. If \(\angle G=53^{\circ}\) then \(\angle H=\)?
If the following angle pairs are supplementary, then what is the measure of the missing angle?
5. If \(\angle A=40^{\circ}\) then \(\angle B=\)?
6. If \(\angle A=75^{\circ}\) then \(\angle B=\)?
7. If \(\angle C=110^{\circ}\) then \(\angle F=\)?
8. If \(\angle D=125^{\circ}\) then \(\angle E=\)?
9. If \(\angle M=10^{\circ}\) then \(\angle N=\)?
10. If \(\angle O=157^{\circ}\) then \(\angle P=\)?
Define the following types of angle pairs.
11. Vertical angles
12. Adjacent angles
13. Complementary angles
14. Supplementary angles
15. Interior angles
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.4.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Adjacent Angles | Two angles are adjacent if they share a side and vertex. The word 'adjacent' means 'beside' or 'next-to'. |
| Angle | A geometric figure formed by two rays that connect at a single point or vertex. |
| Intersecting lines | Intersecting lines are lines that cross or meet at some point. |
| Parallel | Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. |
| Perpendicular lines | Perpendicular lines are lines that intersect at a \(90^{\circ}\) angle. |
| Straight angle | A straight angle is a straight line equal to \(180^{\circ}\). |
Additional Resources
Interactive Element
Video: Complementary, Supplementary, and Vertical Angles
Practice:Angle Properties and Theorems