1.14: Complementary Angles
- Page ID
- 2128
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two angles that add up to 90 degrees.
Two angles are complementary if they add up to \(90^{\circ}\). Complementary angles do not have to be congruent or adjacent.
What if you were given two angles of unknown size and were told they are complementary? How would you determine their angle measures?
Example \(\PageIndex{1}\)
Find the measure of an angle that is complementary to \(\angle ABC\) if \(m \angle ABC\) is \(82^{\circ}\).
Solution
\(90^{\circ}−82^{\circ}=8^{\circ}\).
Example \(\PageIndex{2}\)
Find the measure of an angle that is complementary to \(\angle ABC\) if \(m\angle ABC\) is \(12^{\circ}\).
Solution
\(90^{\circ}−12^{\circ}=78^{\circ}\).
Example \(\PageIndex{3}\)
The two angles below are complementary. \(m \angle GHI=x\). What is \(x\)?
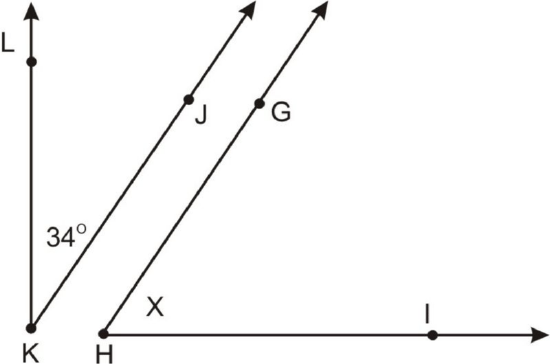Figure \(\PageIndex{1}\)Solution
Because the two angles are complementary, they add up to \(90^{\circ}\). Make an equation.
\(x+34^{\circ}=90^{\circ}\)
\(x=56^{\circ}\)
Example \(\PageIndex{4}\)
The two angles below are complementary. Find the measure of each angle.
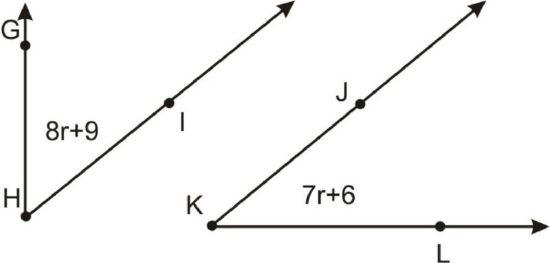Figure \(\PageIndex{2}\Solution
The two angles add up to \(90^{\circ}\). Make an equation.
\((8r+9)+(7r+6)=90^{\circ}\)
\((15r+15)=90^{\circ}\)
\(15r=75^{\circ}\)
\(r=5^{\circ}\)
However, you need to find each angle. Plug r back into each expression.
(m\angle GHI=8(5^{\circ})+9^{\circ}=49^{\circ}\)
\(m \angle JKL=7(5^{\circ})+6^{\circ}=41^{\circ}\)
Example \(\PageIndex{5}\)
Find the measure of an angle that is complementary to \(\angle MRS\) if \(m \angle MRS\) is \(70^{\circ}\).
Solution
Because complementary angles have to add up to \(90^{\circ}\), the other angle must be \(90^{\circ}−70^{\circ}=20^{\circ}\).
Review
Find the measure of an angle that is complementary to \(\angle ABC\) if \(m \angle ABC\) is:
- \(4^{\circ}\)
- \(89^{\circ}\)
- \(54^{\circ}\)
- \(32^{\circ}\)
- \(27^{\circ}\)
- \((x+y)^{\circ}\)
- \(z^{\circ}\)
Use the diagram below for exercises 8-9. Note that \(\overline{NK} \perp \overleftrightarrow{IL}\).
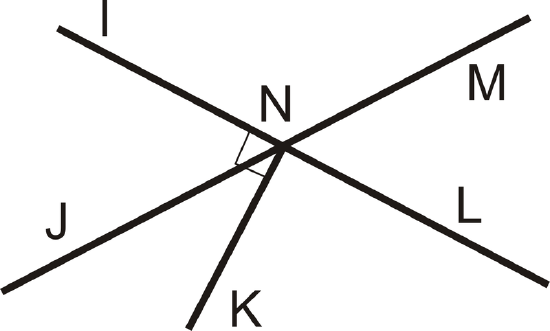Figure \(\PageIndex{3}\)- Name two complementary angles.
- If \(m \angle INJ=63^{\circ}\), find \(m \angle KNJ\).
For 10-11, determine if the statement is true or false.
- Complementary angles add up to \(180^{\circ}\).
- Complementary angles are always \(45^{\circ}\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.7.
Resource
Vocabulary
| Term | Definition |
|---|---|
| complementary angles | Two angles are complementary if they add up to \(90^{\circ}\). |
Additional Resource
Interactive Element
Video: Complementary, Supplementary, and Vertical Angles
Activities: Complementary Angles Discussion Questions
Study Aids: Angles Study Guide
Practice: Complementary Angles
Real World: Complementary Angles