1.15: Supplementary Angles
- Page ID
- 2130
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two angles that add to 180 degrees and when adjacent form a straight line.
Linear Pairs
Two angles are adjacent if they have the same vertex, share a side, and do not overlap. \(\angle PSQ\) and \(\angle QSR\) are adjacent.
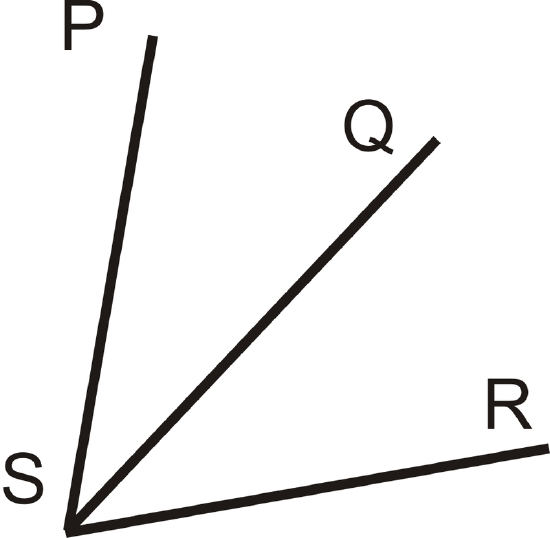Figure \(\PageIndex{1}\)A linear pair is two angles that are adjacent and whose non-common sides form a straight line. If two angles are a linear pair, then they are supplementary (add up to \(180^{\circ}\)). \(\angle PSQ\) and \(\angle QSR\) are a linear pair.
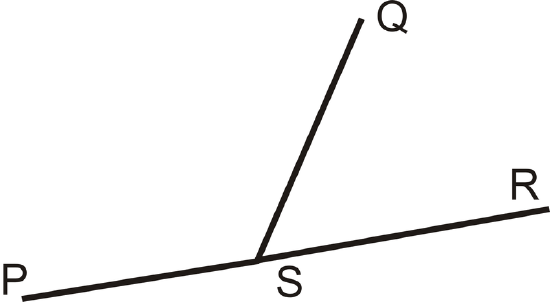Figure \(\PageIndex{2}\)What if you were given two angles of unknown size and were told they form a linear pair? How would you determine their angle measures?
For Example \(\PageIndex{1}\) and \(\PageIndex{2}\), use the diagram below. Note that \(\overline{NK} \perp \overleftrightarrow{IL}\).
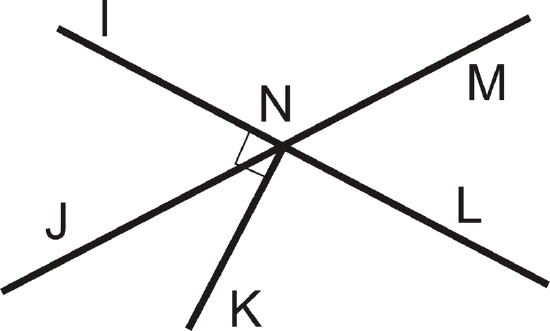Figure \(\PageIndex{3}\)Example \(\PageIndex{1}\)
Name one linear pair of angles.
Solution
\(\angle MNL\) and \(\angle LNJ\)
Example \(\PageIndex{2}\)
What is \(m \angle INL\)?
Solution
\(180^{\circ}\)
Example \(\PageIndex{3}\)
What is the measure of each angle?
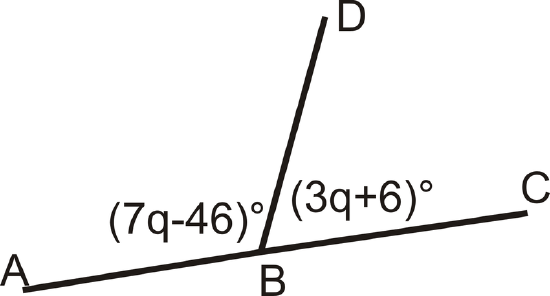Figure \(\PageIndex{4}\)Solution
These two angles are a linear pair, so they add up to \(180^{\circ}\).
\((7q−46)^{\circ}+(3q+6)^{\circ}=180^{\circ}\)
\(10q−40^{\circ}=220^{\circ}\)
\(10q=180^{\circ}\)
\(q=22^{\circ}\)
Plug in q to get the measure of each angle.
\(m \angle ABD=7(22^{\circ})−46^{\circ}=108^{\circ} \)
\(m \angle DBC=180^{\circ}−108^{\circ}=72^{\circ}\)
Example \(\PageIndex{4}\)
Are \(\angle CDA\) and \(\angle DAB\) a linear pair? Are they supplementary?
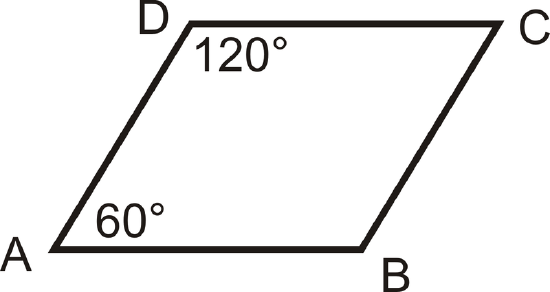Figure \(\PageIndex{5}\)Solution
The two angles are not a linear pair because they do not have the same vertex. They are supplementary because they add up to \(180^{\circ}: 120^{\circ}+60^{\circ}=180^{\circ}\).
Example \(\PageIndex{5}\)
Find the measure of an angle that forms a linear pair with \(\angle MRS\) if \(m \angle MRS\) is \(150^{\circ}\).
Solution
Because linear pairs have to add up to \(180^{\circ}\), the other angle must be \(180^{\circ}−150^{\circ}=30^{\circ}\).
Review
For 1-5, determine if the statement is true or false.
- Linear pairs are congruent.
- Adjacent angles share a vertex.
- Adjacent angles overlap.
- Linear pairs are supplementary.
- Supplementary angles form linear pairs.
For exercise 6, find the value of \(x\).
-
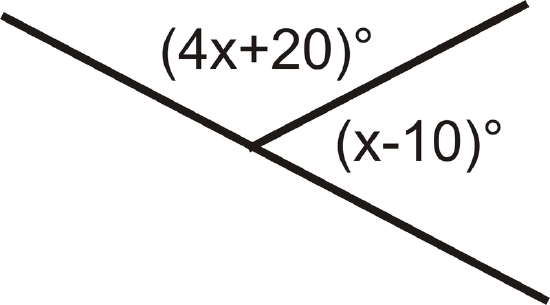Figure \(\PageIndex{6}\)
Find the measure of an angle that forms a linear pair with \(\angle MRS\) if \(m \angle MRS\) is:
- \(61^{\circ}\)
- \(23^{\circ}\)
- \(114^{\circ}\)
- \(7^{\circ}\)
- \(179^{\circ}\)
- \(z^{\circ}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.9.
Vocabulary
| Term | Definition |
|---|---|
| Adjacent Angles | Two angles are adjacent if they share aside and vertex. The word 'adjacent' means 'beside' or 'next-to'. |
| linear pair | Two angles form a linear pair if they are supplementary and adjacent. |
| Diagram | A diagram is a drawing used to represent a mathematical problem. |
Additional Resources
Interactive Element
Video: Complementary, Supplementary, and Vertical Angles
Activities: Supplementary Angles Discussion Questions
Study Aids: Angles Study Guide
Practice: Supplementary Angles
Real World: Supplementary Angles