1.16: Missing Measures of Complementary and Supplementary Angles
- Page ID
- 2131
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find missing angle measures for supplementary or complementary angles.
Let's Think About It
Figure \(\PageIndex{1}\)Marco is building a house. He bought lots of wood to make the frame of the house. He wants right angles for his corners. If he uses a piece of wood that is cut at a \(55^{\circ}\) angle, what must be the angle measure of the other piece of wood that he uses to complete the corner?
In this concept, you will learn how reasoning can help you figure out the measures of missing angles.
Guidance
Some special angle pairs are identified by their sum. If you know the measure of one angle, you can calculate the measure of the second angle. For instance, complementary angles always add up to \(90^{\circ}\). Let’s look at an example.
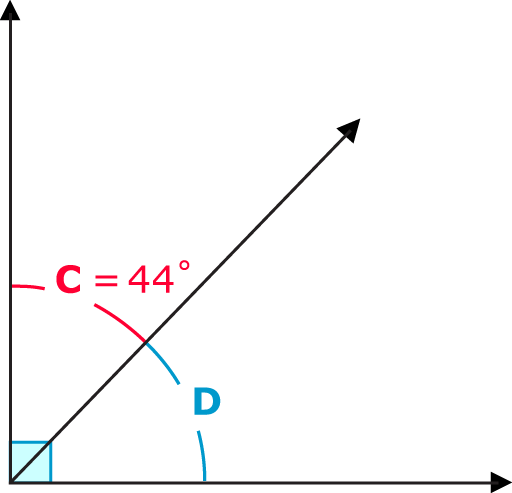Figure \(\PageIndex{2}\)Together, \(C\) and \(D\) form a right angle. Therefore they are complementary, and they add up to \(90^{\circ}\). \(C\) has a measure of \(44^{\circ}\).
To find the measurement of angle \(D\), simply subtract the measure of angle \(C\) from \(90^{\circ}\).
\(\angle C+\angle D=90^{\circ}\)
\(44^{\circ}+\angle D=90^{\circ}\)
\(\angle D=90−44\)
\(\angle D=46^{\circ}\)
Angle \(D\) therefore measures \(46^{\circ}\). You can check the calculation by adding angles \(C\) and \(D\). The sum must be equal to \(90^{\circ}\).
\(44^{\circ}+46^{\circ}=90^{\circ}\)
The same process can be used to find the unknown angle in a pair of supplementary angles. Let's look at another example.
Angles \(P\) and \(Q\) are supplementary angles. If angle \(P\) measures \(112^{\circ}\), what is the measure of angle \(Q\)?
Supplementary angles have a total of \(180^{\circ}\). Subtract the measurement of \(P\), from \(180^{\circ}\) to find the measure of angle \(Q\).
\(\angle P+\angle Q=180^{\circ}\)
\(112^{\circ}+\angle Q=180^{\circ}\)
\(\angle Q=180−112\)
\(\angle Q=68^{\circ}\)
Angle \(Q\) is \(68^{\circ}\). You can check the calculation by adding angles \(P\) and \(Q\). Remember, in order to be supplementary angles, their sum must equal \(180^{\circ}\).
\(68^{\circ}+112^{\circ}=180^{\circ}\)
This process can often be used to find the measure of unknown angles. Use logical reasoning to interpret the information in order to find the unknown measure.
Take a look at the diagram below.
Figure \(\PageIndex{3}\)Guided Practice
Solve the following problem.
What is the measure of angle \(R\)?
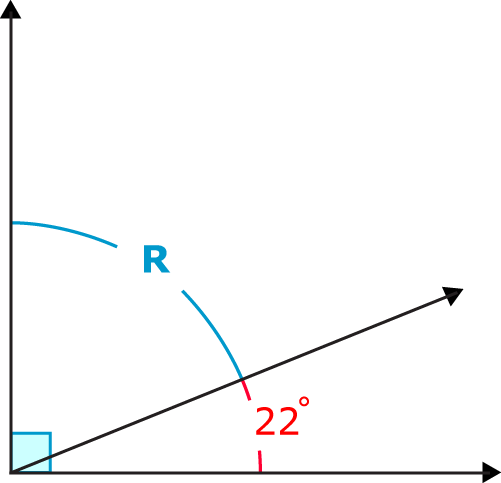Figure \(\PageIndex{4}\)First, set up an equation that represents the relationship between the two angles.
\(R+22=90\)
Next, subtract the given angle from the sum of the two angles.
\(R=90^{\circ}−22^{\circ}\)
Then, calculate the difference.
The difference is \(68^{\circ}\).
The answer is angle \(R=68^{\circ}\).
The measure of the unknown angle is \(68^{\circ}\). You can check your answer by putting this value in for \(R\) in the equation.
\(68+22=90^{\circ}\)
Find the complement or supplement in each example.
Example \(\PageIndex{1}\)
Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(33^{\circ}\). Find the measure of angle \(B\).
Solution
First, set up an equation that represents the relationship between the angles.
\(33^{\circ}+B=90^{\circ}\)
Next, subtract the given angle from the sum of the two angles.
\(B=90^{\circ}−33^{\circ}\)
Then, calculate the difference.
The difference is \(57^{\circ}\).
The answer is angle \(B= 57^{\circ}\).
Example \(\PageIndex{2}\)
Angles \(C\) and \(D\) are supplementary. Angle C is \(59^{\circ}\). Find the measure of angle \(D\).
Solution
First, set up an equation that represents the relationship between the angles.
\(59^{\circ}+D=180^{\circ}\)
Next, subtract the given angle from the sum of the two angles.
\(D=180^{\circ}−59^{\circ}\)
Then, calculate the difference.
The difference is \(121^{\circ}\).
The answer is angle \(D= 121^{\circ}\)
Example \(\PageIndex{3}\)
Angles \(A\) and \(B\) are supplementary. Angle \(A\) is 169^{\circ}. Find the measure of angle \(B\).
Solution
First, set up an equation that represents the relationship between the angles.
\(169^{\circ}+B=180^{\circ}\)
Next, subtract the given angle from the sum of the angles.
\(B=180^{\circ}−169^{\circ}\)
Then, calculate the difference.
The difference is \(11^{\circ}\).
The answer is angle \(B= 11^{\circ}\)
Follow Up
Figure \(\PageIndex{5}\)Remember Marco and his house? If one piece of wood has an angled cut that is \(55^{\circ}\), what is the measure of the angled cut for the second piece of wood?
First, set up an equation that represents the relationship between the two angles.
\(55^{\circ}+M=90^{\circ}\)
Next, subtract the given angle from the sum of the two angles.
\(M=90^{\circ}−55^{\circ}\)
Then calculate the difference.
The difference is \(35^{\circ}\).
The answer is that the second piece of wood is cut at a \(35^{\circ}\) angle.
Video Review
Explore More
Find the measure of missing angle for each pair of complementary or supplementary angles.
1. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(63^{\circ}\). Find the measure of angle \(B\).
2. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(83^{\circ}\). Find the measure of angle \(B\).
3. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(3^{\circ}\). Find the measure of angle \(B\).
4. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(23^{\circ}\). Find the measure of angle \(B\).
5. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(70^{\circ}\). Find the measure of angle \(B\).
6. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(29^{\circ}\). Find the measure of angle \(B\).
7. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(66^{\circ}\). Find the measure of angle \(B\).
8. Angles \(A\) and \(B\) are complementary. Angle \(A\) is \(87^{\circ}\). Find the measure of angle \(B\).
9. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(33^{\circ}\). Find the measure of angle \(B\).
10. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(103^{\circ}\). Find the measure of angle \(B\).
11. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(73^{\circ}\). Find the measure of angle \(B\).
12. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(78^{\circ}\). Find the measure of angle \(B\).
13. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(99^{\circ}\). Find the measure of angle \(B\).
14. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(110^{\circ}\). Find the measure of angle \(B\).
15. Angles \(A\) and \(B\) are supplementary. Angle \(A\) is \(127^{\circ}\). Find the measure of angle \(B\).
Vocabulary
| Term | Definition |
|---|---|
| Acute Angle | An acute angle is an angle with a measure of less than 90 degrees. |
| Complementary angles | Complementary angles are a pair of angles with a sum of 90∘. |
| Obtuse angle | An obtuse angle is an angle greater than 90 degrees but less than 180 degrees. |
| Straight angle | A straight angle is a straight line equal to 180∘. |
| Supplementary angles | Supplementary angles are two angles whose sum is 180 degrees. |
Additional Resources
Interactive Element
Video: Complementary, Supplementary, and Vertical Angles
Practice: Missing Measures of Complementary and Supplementary Angles
Real World: Leaning Towers