1.17: Vertical Angles
- Page ID
- 2127
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Understand that vertical angles are opposite each other and have the same measure.
Vertical angles are two non-adjacent angles formed by intersecting lines. \(\angle 1\) and \(\angle 3\) are vertical angles and \(\angle 2\) and \(\angle 4\) are vertical angles.
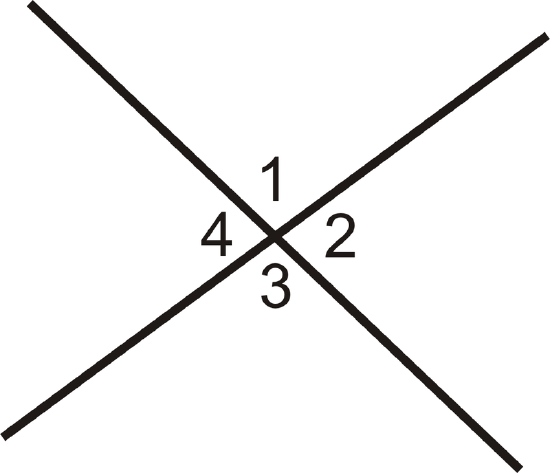Figure \(\PageIndex{1}\)The Vertical Angles Theorem states that if two angles are vertical angles, then they are congruent.
What if you were given two angles of unknown size and were told they are vertical angles? How would you determine their angle measures?
Example \(\PageIndex{1}\)
Find the value of \(x\).
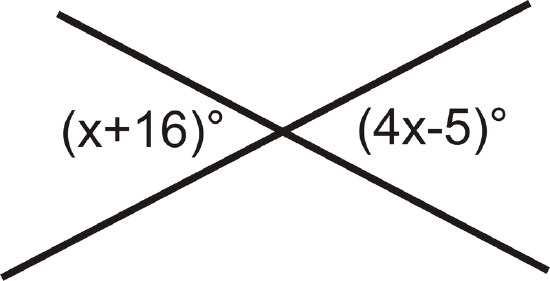Figure \(\PageIndex{2}\)Solution
Vertical angles are congruent, so set the angles equal to each other and solve for \(x\).
\(x+16=4x−5\)
\(3x=21\)
\(x=7^{\circ}\)
Example \(\PageIndex{2}\)
Find the value of \(y\).
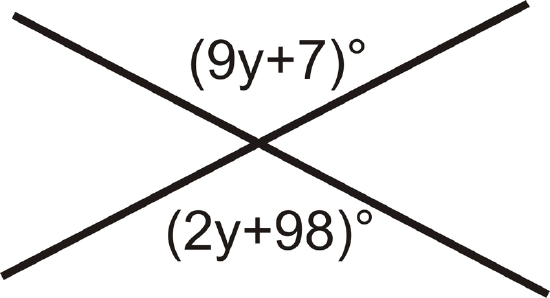Figure \(\PageIndex{3}\)Solution
Vertical angles are congruent, so set the angles equal to each other and solve for \(y\).
\(9y+7=2y+98\)
\(7y=91\)
\(y=13^{\circ}\)
Example \(\PageIndex{3}\)
Find \(m\angle 1\).
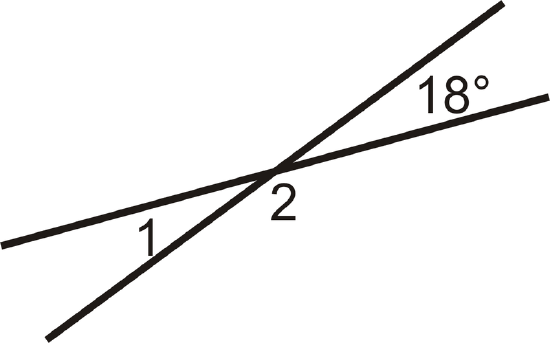Figure \(\PageIndex{4}\)Solution
\(\angle 1\) is vertical angles with \(18^{\circ}\), so \(m\angle 1=18^{\circ}.
Example \(\PageIndex{4}\)
If \angle ABC and \angle DEF are vertical angles and \(m\angle ABC=(4x+10)^{\circ} and \(m\angle DEF=(5x+2)^{\circ}, what is the measure of each angle?
Solution
Vertical angles are congruent, so set the angles equal to each other and solve for x. Then go back to find the measure of each angle.
\(4x+10=5x+2\)
\(x=8\)
So, \(m\angle ABC=m\angle DEF=(4(8)+10)^{\circ}=42^{\circ}\)
Example \(\PageIndex{5}\)
True or false: vertical angles are always less than 90^{\circ}.
Solution
This is false, you can have vertical angles that are more than 90^{\circ}. Vertical angles are less than 180^{\circ}.
Review
Use the diagram below for exercises 1-2. Note that \(\overline{NK} \perp \overleftrightarrow{IL}\).
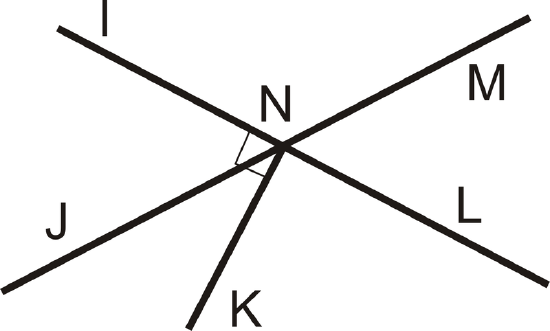Figure \(\PageIndex{5}\)- Name one pair of vertical angles.
- If \(m\angle INJ=63^{\circ}\), find \(m\angle MNL\).
For exercise 3, determine if the statement is true or false.
- Vertical angles have the same vertex.
- If \(\angle ABC\) and \(\angle DEF\) are vertical angles and \(m\angle ABC=(9x+1)^{\circ}\) and \(m\angle DEF=(5x+29)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\) and \(\angle DEF\) are vertical angles and \(m\angle ABC=(8x+2)^{\circ}\) and \(m\angle DEF=(2x+32)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\) and \(\angle DEF\) are vertical angles and \(m\angle ABC=(x+22)^{\circ}\) and \(m\angle DEF=(5x+2)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\) and \(\angle DEF\) are vertical angles and \(m\angle ABC=(3x+12)^{\circ}\) and \(m\angle DEF=(7x)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\) and \(\angle DEF\) are vertical angles and \(m\angle ABC=(5x+2)^{\circ}\) and \(m\angle DEF=(x+26)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\) and \(\angle DEF\)are vertical angles and \(m\angle ABC=(3x+1)^{\circ}\) and \(m\angle DEF=(2x+2)^{\circ}\), what is the measure of each angle?
- If \(\angle ABC\)and \(\angle DEF\) are vertical angles and \(m\angle ABC=(6x−3)^{\circ}\) and \(m\angle DEF=(5x+1)^{\circ}\), what is the measure of each angle?
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.10.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Vertical Angles | Vertical angles are a pair of opposite angles created by intersecting lines. |
| Vertical Angles Theorem | The Vertical Angles Theorem states that if two angles are vertical, then they are congruent. |
Additional Resources
Interactive Element
Video: Complementary, Supplementary, and Vertical Angles
Activities: Vertical Angles Discussion Questions
Study Aids: Angles Study Guide
Practice: Vertical Angles
Real World: Vertical Angles