1.18: Classify Polygons
- Page ID
- 2129
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Categories of polygons based on the number of sides, and whether they are concave or convex.
Polygons
A polygon is any closed, 2-dimensional figure that is made entirely of line segments that intersect at their endpoints. Polygons can have any number of sides and angles, but the sides can never be curved. The segments are called the sides of the polygons, and the points where the segments intersect are called vertices.
Polygons can be either convex or concave. The term concave refers to a cave, or the polygon is “caving in”. All stars are concave polygons.
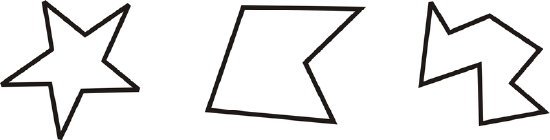 Figure \(\PageIndex{1}\)
Figure \(\PageIndex{1}\)A convex polygon does not cave in. Convex polygons look like:
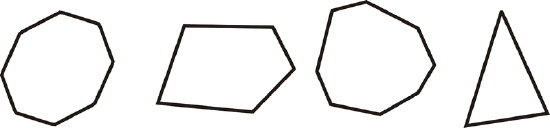 Figure \(\PageIndex{2}\)
Figure \(\PageIndex{2}\)A diagonal is a non-side line segment that connects two vertices of a convex polygon.
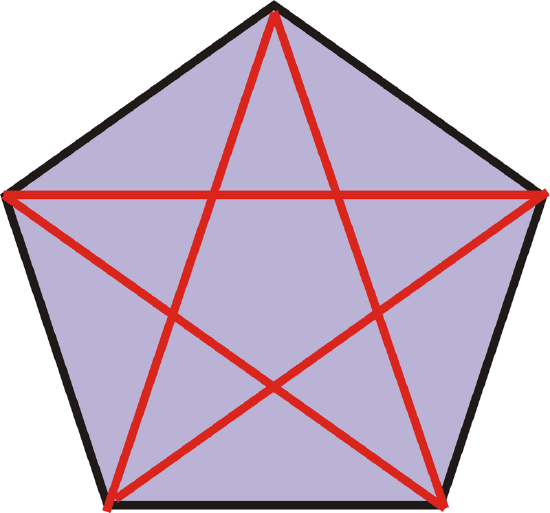 Figure \(\PageIndex{3}\)
Figure \(\PageIndex{3}\)The red line segments are all diagonals. This pentagon has 5 diagonals.
Whether a polygon is convex or concave, it is always named by the number of sides. Explore the relationship between the number of sides of a convex polygon and its diagonals. Can you complete the table?
| Polygon Name | Number of Sides | Number of Diagonals | Convex Example |
|---|---|---|---|
| Triangle | 3 | 0 |
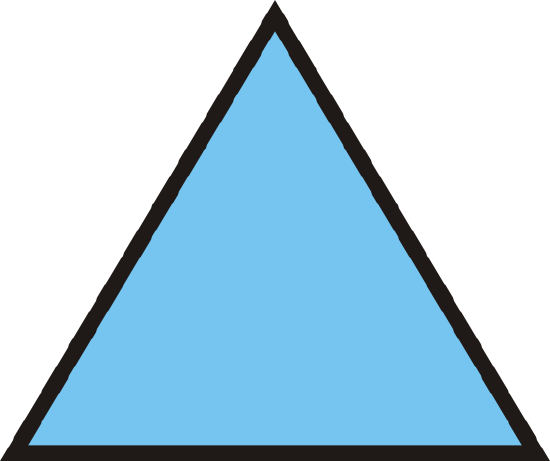 Figure \(\PageIndex{4}\) Figure \(\PageIndex{4}\) |
| Quadrilateral | 4 | 2 |
 Figure \(\PageIndex{5}\) Figure \(\PageIndex{5}\) |
| Pentagon | 5 | 5 |
 Figure \(\PageIndex{6}\) Figure \(\PageIndex{6}\) |
| Hexagon | 6 | 9 |
 Figure \(\PageIndex{7}\) Figure \(\PageIndex{7}\) |
| Heptagon | 7 | ? |
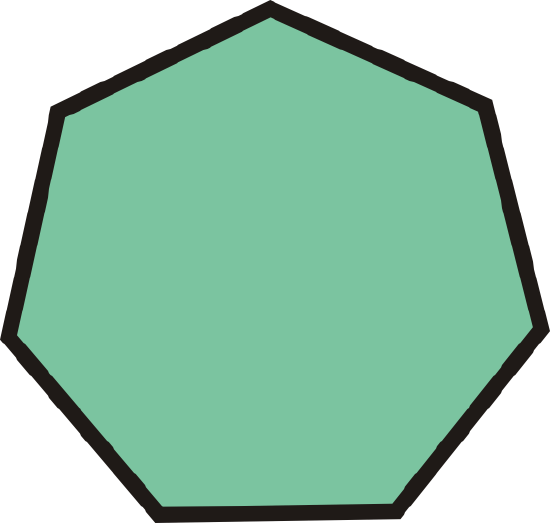 Figure \(\PageIndex{8}\) Figure \(\PageIndex{8}\) |
| Octagon | 8 | ? |
 Figure \(\PageIndex{9}\) Figure \(\PageIndex{9}\) |
| Nonagon | 9 | ? |
 Figure \(\PageIndex{10}\) Figure \(\PageIndex{10}\) |
| Decagon | 10 | ? |
 Figure \(\PageIndex{11}\) Figure \(\PageIndex{11}\) |
| Undecagon or hendecagon | 11 | ? |
 Figure \(\PageIndex{12}\) Figure \(\PageIndex{12}\) |
| Dodecagon | 12 | ? |
 Figure \(\PageIndex{13}\) Figure \(\PageIndex{13}\) |
| n-gon | n (where n>12) | ? |
 Figure \(\PageIndex{14}\) Figure \(\PageIndex{14}\) |
What if you were told how many sides a polygon has? How would you describe the polygon based on that information?
Example \(\PageIndex{1}\)
Which of the figures below is a polygon?
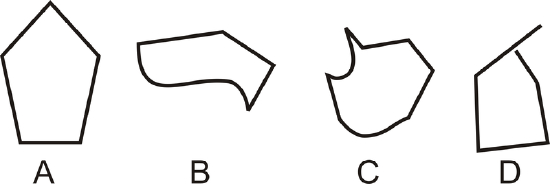 Figure \(\PageIndex{15}\)
Figure \(\PageIndex{15}\)Solution
The easiest way to identify the polygon is to identify which shapes are not polygons. B and C each have at least one curved side, so they are not be polygons. D has all straight sides, but one of the vertices is not at the endpoint, so it is not a polygon. A is the only polygon.
Example \(\PageIndex{2}\)
Determine if the shapes below are convex or concave.
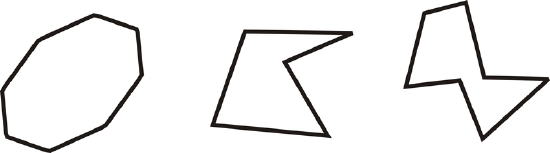 Figure \(\PageIndex{16}\)
Figure \(\PageIndex{16}\)Solution
To see if a polygon is concave, look at the polygons and see if any angle “caves in” to the interior of the polygon. The first polygon does not do this, so it is convex. The other two do, so they are concave.
Example \(\PageIndex{3}\)
Name the three polygons below by their number of sides and if it is convex or concave.
 Figure \(\PageIndex{17}\)
Figure \(\PageIndex{17}\)Solution
The pink polygon is a concave hexagon (6 sides).
The green polygon convex pentagon (5 sides).
The yellow polygon is a convex decagon (10 sides).
Example \(\PageIndex{4}\)
Draw a 7-sided polygon, also called a heptagon. How many diagonals does a heptagon have?
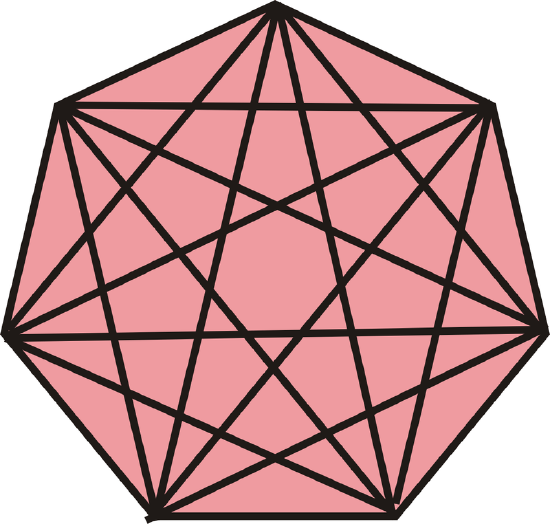 Figure \(\PageIndex{18}\)
Figure \(\PageIndex{18}\)Solution
First, draw the heptagon. Drawing in all the diagonals and counting them, we see there are 14.
Example \(\PageIndex{5}\)
True or false: A quadrilateral is always a square.
Solution
False. Only quadrilaterals with four congruent sides and four right angles will be squares. There are many quadrilaterals (such as rectangles, kites, parallelograms, trapezoids, etc.) that are not necessarily squares.
Review
In problems 1-6, name each polygon in as much detail as possible.
-
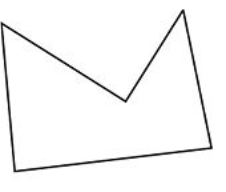 Figure \(\PageIndex{19}\)
Figure \(\PageIndex{19}\) -
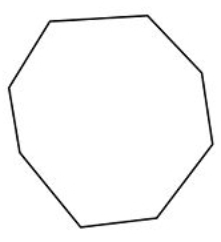 Figure \(\PageIndex{20}\)
Figure \(\PageIndex{20}\) -
 Figure \(\PageIndex{21}\)
Figure \(\PageIndex{21}\) -
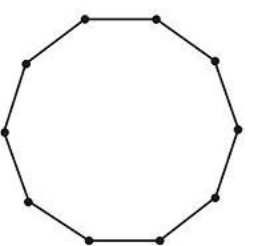 Figure \(\PageIndex{22}\)
Figure \(\PageIndex{22}\) -
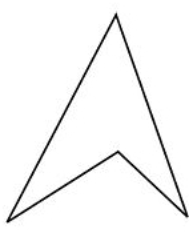 Figure \(\PageIndex{23}\)
Figure \(\PageIndex{23}\) -
 Figure \(\PageIndex{24}\)
Figure \(\PageIndex{24}\) - Explain why the following figures are NOT polygons:
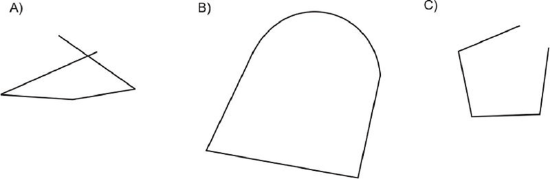 Figure \(\PageIndex{25}\)
Figure \(\PageIndex{25}\) - How many diagonals can you draw from one vertex of a pentagon? Draw a sketch of your answer.
- How many diagonals can you draw from one vertex of an octagon? Draw a sketch of your answer.
- How many diagonals can you draw from one vertex of a dodecagon?
- Determine the number of total diagonals for an octagon, nonagon, decagon, undecagon, and dodecagon.
For 12-14, determine if the statement is true or false.
- A polygon must be enclosed.
- A star is a convex polygon.
- A 5-point star is a decagon.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.12.
Resource
Vocabulary
| Term | Definition |
|---|---|
| diagonal (of a polygon) | A non-side line segment that connect two vertices of a convex polygon. |
| Polygon | A polygon is a simple closed figure with at least three straight sides. |
| Concave | A concave polygon has at least one interior angle greater than 180 degrees. A common way to identify a concave polygon is to look for a "caved-in" side of the polygon. |
| Convex | A convex polygon contains no interior angles greater than 180 degrees. |
| Diagonal | A diagonal is a line segment in a polygon that connects nonconsecutive vertices |
| Exterior angles | An exterior angle is the angle formed by one side of a polygon and the extension of the adjacent side. |
| Interior angles | Interior angles are the angles inside a figure. |
| Regular Polygon | A regular polygon is a polygon with all sides the same length and all angles the same measure. |
| Vertices | Vertices are points where line segments intersect. |
| Equilateral | A polygon is equilateral if all of its sides are the same length. |
Additional Resource
Interactive Element
Video: Sum of Interior Angles of a Polygon
Activities: Polygon Classification Discussion Questions
Study Aids: Polygons Study Guide
Practice: Classify Polygons
Real World: Nature's Polygons

