Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.3: Definition of Line segments

Last updated

Nov 28, 2020
Save as PDF
- 1.2: Shapes
- 1.4: Midpoints and Segment Bisector

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Identify the Positive length between points.

Measuring Distance Between Two Points

Distance is the measure of length between two points. To measure is to determine how far apart two geometric objects are. The most common way to measure distance is with a ruler. Inch-rulers are usually divided up by eighth-inch (or 0.125 in) segments. Centimeter rulers are divided up by tenth-centimeter (or 0.1 cm) segments. Note that the distance between two points is the absolute value of the difference between the numbers shown on the ruler. This implies that you do not need to start measuring at “0”, as long as you subtract the first number from the second.

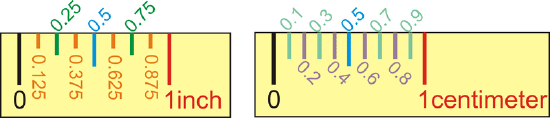f-d_3df110041aecbc080eb9d5514613b2ee8d11e08086a9b6e01bd2dae0+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{1}$

The segment addition postulate states that if $A$ , $B$ , and $C$ are collinear and $B$ is between $A$ and $C$ , then $AB+BC=AC$ .

f-d_436c14cc166a2505476266587ffcedd332512e64c748b31a4dab6962+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{2}$

You can find the distances between points in the $x–y$ plane if the lines are horizontal or vertical. If the line is vertical, find the change in the $y$ −coordinates. If the line is horizontal, find the change in the $x$ −coordinates.

Suppose you want to measure your height, but the measuring tape you have is old and the end is broken off. If the tape now starts at 6 cm and reads 138 cm from the floor to the top of your head, how tall are you?

Example $\PageIndex{1}$

What is the distance marked on the ruler below? The ruler is in centimeters.

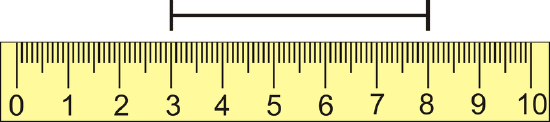f-d_c2b23827e0519a2a87a9399f5e59bfffada756d2f97b299c8e1e8e7f+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{3}$

Solution

Subtract one endpoint from the other. The line segment spans from 3 cm to 8 cm.

$|8−3|=|5|=5$

The line segment is 5 cm long. Notice that you also could have done

$|3−8|=|−5|=5$ .

Example $\PageIndex{2}$

Make a sketch of $\overline{OP}$ , where $Q$ is between $O$ and $P$ .

Solution

Draw $\overline{OP}$ first, then place $Q$ on the segment.

f-d_0bc9da2cee402168f41d62663d344677216cd065a02c2b68959083c2+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{4}$

Example $\PageIndex{3}$

What is the distance between the two points shown below?

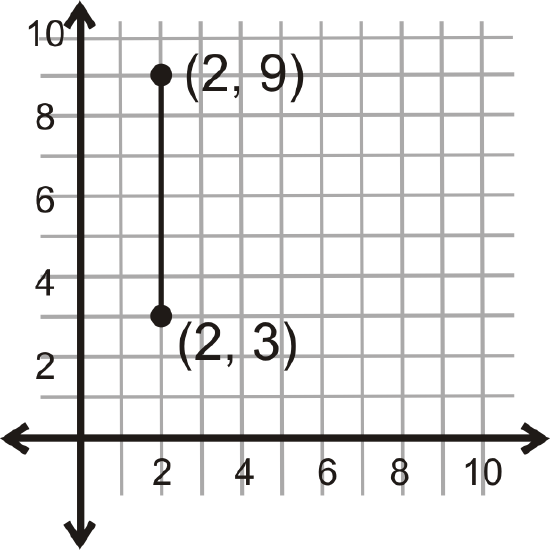f-d_7659965eff21eeea21f846ce8e27a674148b4593a6313dac7af05a35+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{5}$

Solution

Because this line is vertical, look at the change in the $y$ -coordinates.

$|9−3|=|6|=6$

The distance between the two points is 6 units.

Example $\PageIndex{4}$

In the picture from Example 2, if $OP=17$ and $QP=6$ , what is $OQ$ ?

Solution

$OQ+QP=OP$

$OQ+6=17$

$OQ=17−6$

$OQ=11$

Example $\PageIndex{5}$

What is the distance between the two points shown below?

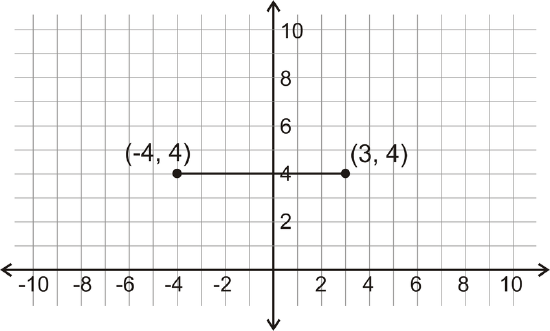f-d_1756425b14d9e56a0049874e50ff4e1cab6ef1f28aceeb95cb14c215+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{6}$

Solution

Because this line is horizontal, look at the change in the $x$ -coordinates.

$|(−4)−3|=|−7|=7$

The distance between the two points is 7 units.

Review

For 1-4, use the ruler in each picture to determine the length of the line segment.

Figure $\PageIndex{7}$
Figure $\PageIndex{8}$
Figure $\PageIndex{9}$
Figure $\PageIndex{10}$
Make a sketch of $\overline{BT}$ , with $A$ between $B$ and $T$ .
If O is in the middle of $\overline{LT}$ , where exactly is it located? If $LT=16 cm$ , what is $LO$ and $OT$ ?
For three collinear points, A between T and Q:
1. Draw a sketch.
2. Write the Segment Addition Postulate for your sketch.
3. If $AT=10$ in and $AQ=5$ in, what is $TQ$ ?
For three collinear points, M between H and A:
1. Draw a sketch.
2. Write the Segment Addition Postulate for your sketch.
3. If $HM=18 cm$ and $HA=29 cm$ , what is $AM$ ?
For three collinear points, I between M and T:
1. Draw a sketch.
2. Write the Segment Addition Postulate for your sketch.
3. If $IT=6 cm$ and $MT=25 cm$ , what is $AM$ ?
Make a sketch that matches the description: B is between $A$ and $D$ . $C$ is between $B$ and $D$ . $AB=7 cm$ , $AC=15 cm$ , and $AD=32 cm$ . Find $BC$ , $BD$ , and $CD$ .
Make a sketch that matches the description: $E is between \(F$ and $G$ . $H$ is between $F$ and $E$ . $FH=4 in$ , $EG=9 in$ , and $FH=HE$ . Find $FE$ , $HG$ , and $FG$ .

For 12 and 13, Suppose $J$ is between $H$ and $K$ . Use the Segment Addition Postulate to solve for $x$ . Then find the length of each segment.

$HJ=4x+9$ , $JK=3x+3$ , $KH=33$
$HJ=5x−3$ , $JK=8x−9$ , $KH=131$

For 14-17, determine the vertical or horizontal distance between the two points.

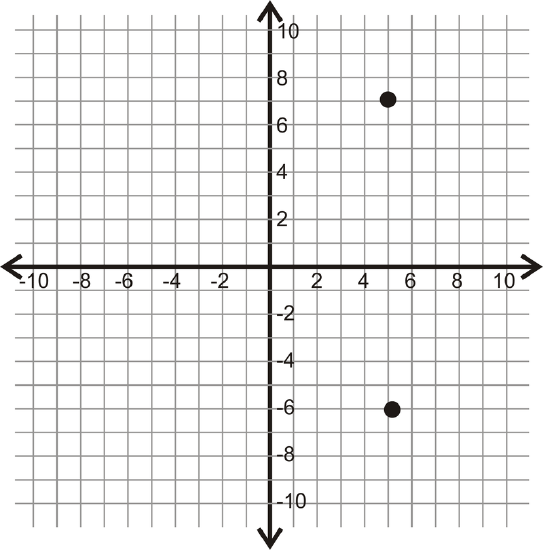Figure $\PageIndex{11}$
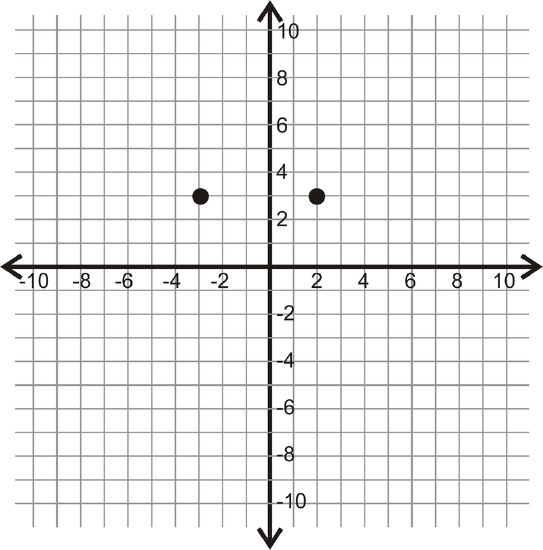Figure $\PageIndex{12}$
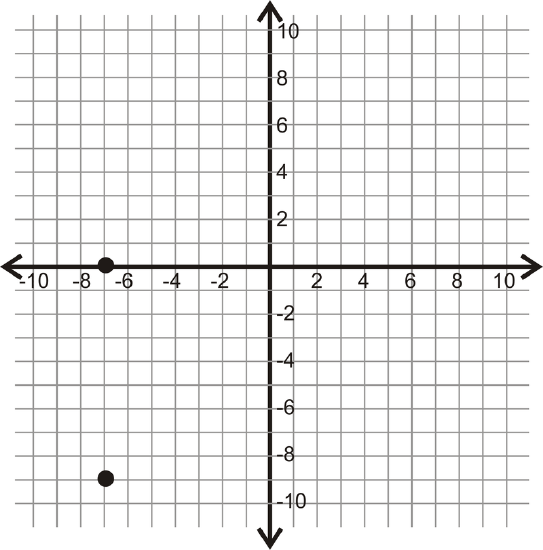Figure $\PageIndex{13}$
F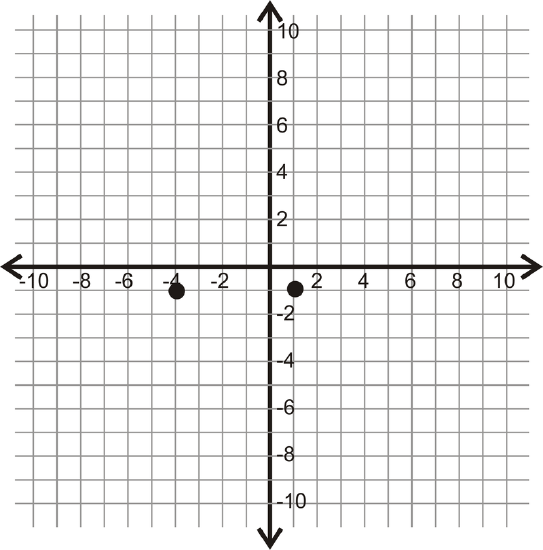Figure $\PageIndex{14}$
Make a sketch of: $S$ is between $T$ and $V$ . $R$ is between $S$ and $T$ . $TR=6$ , $RV=23$ , and $TR=SV$ .
Find $SV$ , $TS$ , $RS$ and $TV$ from #18.
For $\overline{HK}$ , suppose that $J$ is between $H$ and $K$ . If $HJ=2x+4$ , $JK=3x+3$ , and $KH=22$ , find $x$ .

Vocabulary

Term	Definition
distance	Distance is the measure of length between two points.
Absolute Value	The absolute value of a number is the distance the number is from zero. Absolute values are never negative.
measure	To measure distance is to determine how far apart two geometric objects are by using a number line or ruler.

Additional Resources

Interactive Element

Video: Ruler Postulate and the Segment Addition Postulate

Activities: Distance Between Two Points Discussion Questions

Study Aids: Segments Study Guide

Practice: Definition of Line Segment

Real World: Distance Between Two Points

Measuring Distance Between Two Points

Review

Vocabulary

Additional Resources

Support Center

How can we help?