3.1: Line Types
- Page ID
- 2184
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify parallel, perpendicular and intersecting lines.
Parallel and Perpendicular Lines
Victoria is on a class field trip. While riding over a bridge, she notices that the road and the structure of the bridge make a variety of lines. She believes that the posts of the bridge are perpendicular to the road. What can she say to prove this to her classmates?
In this concept, you will learn how to identify parallel, intersecting and perpendicular lines.
Identifying Parallel and Perpendicular Lines
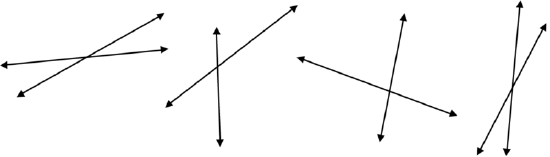
Lines exist in space. Two lines intersect when they cross each other. Because all lines are straight, intersecting lines can only cross each other once. Look at the examples below. Imagine the lines extend beyond the picture, on forever.
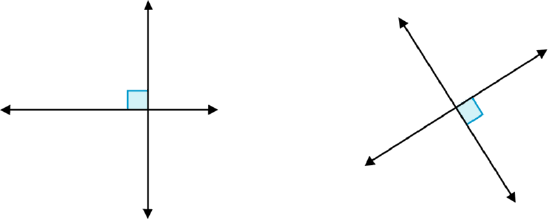
Two lines that form right angles when they intersect are perpendicular lines. All four angles formed by the perpendicular lines measure \(90^{\circ}\). If any of the four angles is marked with the small box, the lines are perpendicular. Take a look at the perpendicular lines below.
Lines that never intersect are parallel lines. Parallel lines do not form any angles. Parallel lines look like railroad tracks: they are always the same distance apart, running next to each other.
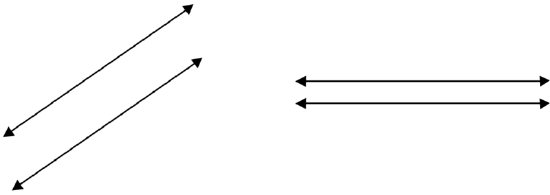Figure \(\PageIndex{4}\)Identify whether the pairs of lines are parallel, perpendicular, or intersecting.
Figure \(\PageIndex{5}\)First, look to see if the lines intersect.
The lines do not intersect.
Next, determine if the lines would intersect if they were extended.
No
Then, label the lines as parallel, perpendicular or intersecting.
The lines are parallel.
The answer is that the lines are parallel.
Figure \(\PageIndex{6}\)First, look to see if the lines intersect.
The lines do intersect.
Next, determine if the lines intersect at a right angle.
The lines do not intersect at a right angle.
Then, label the lines as parallel, perpendicular or neither.
The lines are intersecting.
The answer is that the lines are intersecting but not perpendicular.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Victoria and the bridge.
As she rides across the bridge, she notices the different lines. What can she say to prove that the posts are perpendicular to the road?
Solution
First, treat the posts and the road like lines. Look to see if the lines intersect.
They do intersect.
Next, determine if the lines intersect the road at a right angle.
The lines do intersect at a right angle.
Then, label the lines as parallel, perpendicular or neither.
The lines are perpendicular.
The answer is that the lines are perpendicular.
Example \(\PageIndex{2}\)
Identify whether the pair of lines are parallel, perpendicular or intersecting.
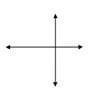Figure \(\PageIndex{7}\)Solution
First, look to see if the lines intersect.
The lines do intersect.
Next, determine if the lines intersect at a right angle.
Yes
Then, label the lines as parallel, perpendicular or intersecting.
Perpendicular.
The answer is that the lines are perpendicular.
Example \(\PageIndex{3}\)
Identify each pair of lines as parallel, perpendicular or neither.
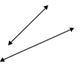Figure \(\PageIndex{8}\)Solution
First, look to see if the lines intersect.
The lines will intersect if they are extended.
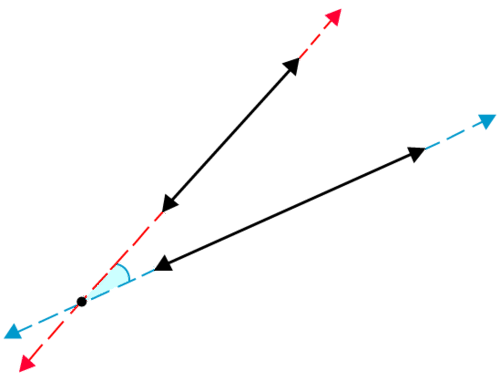Figure \(\PageIndex{9}\)Next, determine if the lines intersect at a right angle.
The lines do not intersect at a right angle.
Then label the lines as parallel, perpendicular or neither.
Intersecting.
The answer is that the lines are intersecting but not perpendicular.
Example \(\PageIndex{4}\)
Figure \(\PageIndex{10}\)Do the two white bars form parallel lines, perpendicular lines or intersecting?
Solution
First, look to see if the bars intersect.
The bars do not intersect.
Next, determine if the bars would intersect if they were extended.
No.
Then, label the lines as parallel, perpendicular or intersecting.
The lines are parallel.
The answer is that the lines are parallel.
Example \(\PageIndex{5}\)
Jeff traces the left side of a standard book and the right side of the book. When he removes the book, what type of lines will be have: parallel, perpendicular or intersecting?
Solution
First, think about a standard book. Do these two sides of a standard book intercept?
The sides do not intersect.
Next, determine if the lines will intersect if they are extended.
No, the lines will not intersect if they are extended.
Then, label the lines as parallel, perpendicular or neither.
The lines are parallel.
The answer is that the lines are parallel.
Review
Use what you have learned to answer each question true or false.
- Adjacent angles are also supplementary angles.
- Vertical angles are complementary angles.
- If one adjacent angle is \(100^{\circ}\), then its angle pair is also \(100^{\circ}\).
- Vertical angles have the same measure.
- Vertical angles and corresponding angles are located in the same position.
- You can have corresponding angles when you only have two intersecting lines.
- Corresponding angles are in the same place given the intersection.
- Parallel lines will never intersect.
- Perpendicular lines intersect at a 90 degree angle.
Tell whether each picture shows parallel or intersecting lines.
-
Figure \(\PageIndex{11}\) -
Figure \(\PageIndex{12}\)
Think about each example described below and determine whether the lines would be intersecting or parallel.
- Telephone wires
- The yellow lines down a highway
- Stitches on a sweater
- The sides of a ramp
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.5.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Corresponding Angles | Corresponding angles are two angles that are in the same position with respect to the transversal, but on different lines. |
| Parallel | Two or more lines are parallel when they lie in the same plane and never intersect. These lines will always have the same slope. |
| Perpendicular lines | Perpendicular lines are lines that intersect at a \(90^{\circ}\) angle. |
Additional Resource
Interactive Element
Interactive Element
Video: Perpendicular Lines - Example 1
Practice: Line Types
Real World: A Road Map to Healing