3.6: Alternate Exterior Angles
- Page ID
- 2187
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles on opposite sides of a transversal, but outside the lines it intersects.
Alternate exterior angles are two angles that are on the exterior of \(l\) and \(m\), but on opposite sides of the transversal.
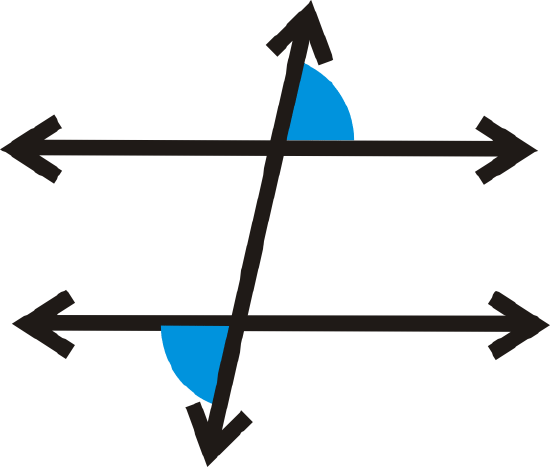
Alternate Exterior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent.
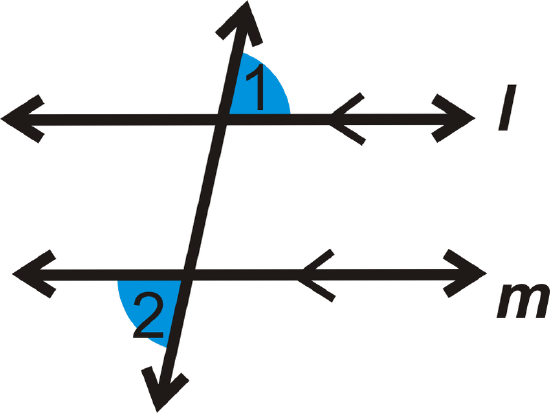
If \(l \parallel m\), then \(\angle 1\cong \angle 2\).
Converse of the Alternate Exterior Angles Theorem: If two lines are cut by a transversal and the alternate exterior angles are congruent, then the lines are parallel.
If
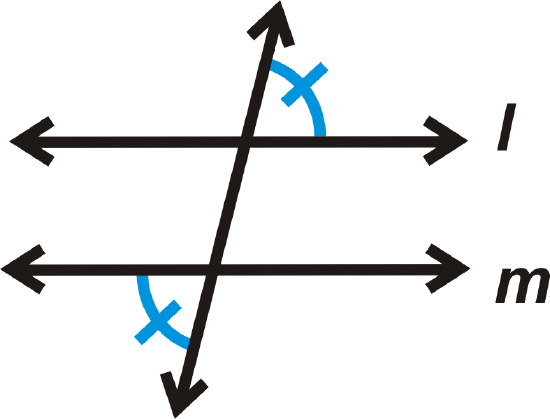
then \(l \parallel m\).
What if you were presented with two angles that are on the exterior of two parallel lines cut by a transversal but on opposite sides of the transversal? How would you describe these angles and what could you conclude about their measures?
For Examples \(\PageIndex{1}\) and \(\PageIndex{2}\), use the following diagram:
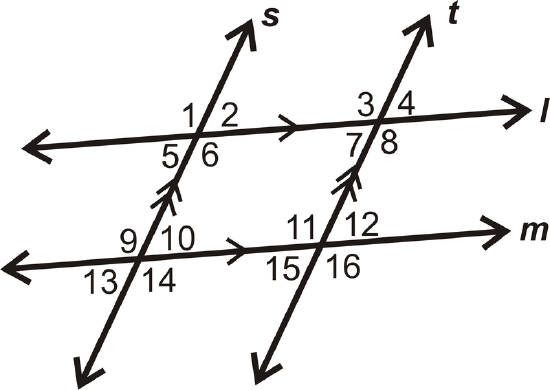
Example \(\PageIndex{1}\)
Give an example of a pair of alternate exterior angles.
Solution
\(\angle 1\) and \(\angle 14\) (many other possibilities)
Example \(\PageIndex{2}\)
Give another example of a pair of alternate exterior angles.
Solution
\(\angle 2\) and \(\angle 13\) (many other possibilities, must be different than answer to Example 1)
Example \(\PageIndex{3}\)
Find the measure of each angle and the value of \)y\).
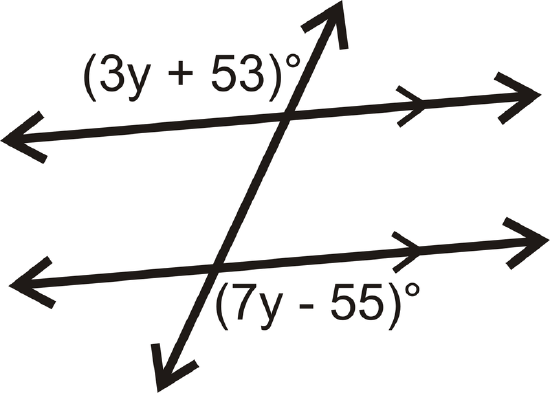
Solution
The angles are alternate exterior angles. Because the lines are parallel, the angles are equal.
\(\begin{align*} (3y+53)^{\circ} &=(7y−55)^{\circ} \\ 108 &=4y \\ 27 &=y \end{align*}\)
If \(y=27, then each angle is \([3(27)+53]^{\circ}=134^{\circ}\).
Example \(\PageIndex{4}\)
The map below shows three roads in Julio’s town.
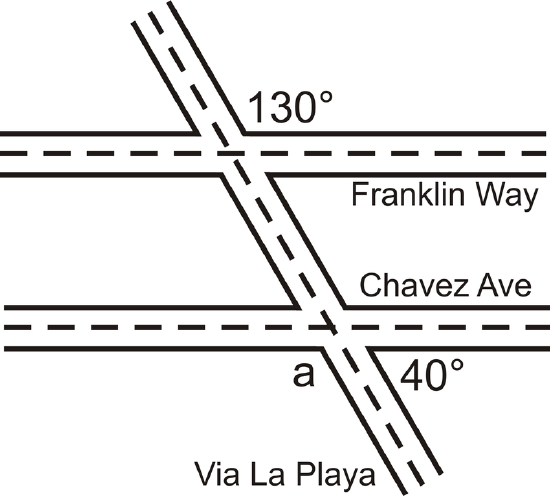
Solution
Julio used a surveying tool to measure two angles at the intersections in this picture he drew (NOT to scale). Julio wants to know if Franklin Way is parallel to Chavez Avenue.
The \(130^{\circ}\) angle and \angle a are alternate exterior angles. If \(m \angle a=130^{\circ}\), then the lines are parallel.
\( \begin{align*} \angle a+40^{\circ} &=180^{\circ} & by\:the \:Linear \:Pair \:Postulate \\ \angle a&=140^{\circ} & \end{align*}\)
\(140^{\circ}\neq 130^{\circ}\), so Franklin Way and Chavez Avenue are not parallel streets.
Example \(\PageIndex{5}\)
Which lines are parallel if \(\angle AFG\cong \angle IJM\)?

Solution
These two angles are alternate exterior angles so if they are congruent it means that \(\overleftrightarrow{CG}\parallel \overleftrightarrow{HK}\).
Review
- Find the value of \(x\) if \(m \angle 1=(4x+35)^{\circ}\), \(m \angle8=(7x−40)^{\circ}\):
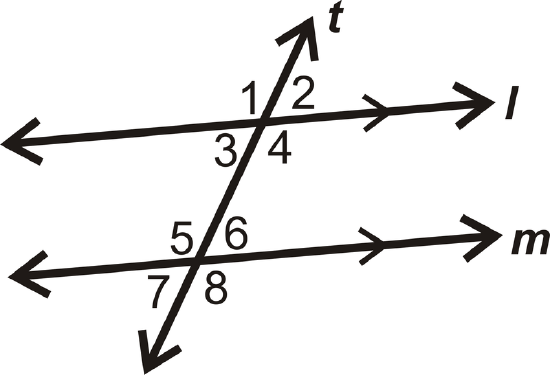
Figure \(\PageIndex{8}\) - Are lines 1 and 2 parallel? Why or why not?
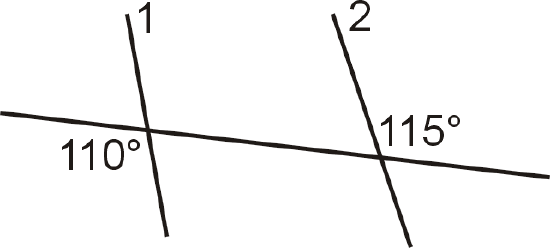
Figure \(\PageIndex{9}\)
For 3-6, what does the value of \(x\) have to be to make the lines parallel?
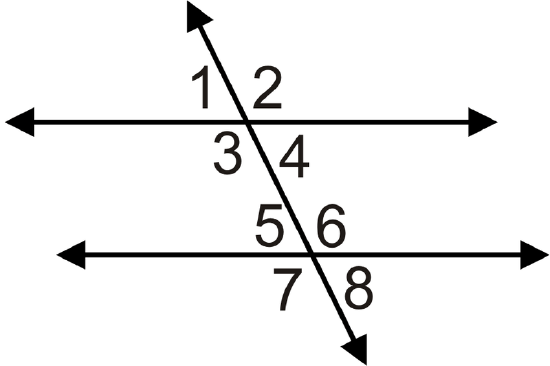
- \(m \angle2=(8x)^{\circ}\) and \(m \angle7=(11x−36)^{\circ}\)
- \(m \angle1=(3x+5)^{\circ}\) and \(m \angle8=(4x−3)^{\circ}\)
- \(m \angle2=(6x−4)^{\circ}\) and \(m \angle7=(5x+10)^{\circ}\)
- \(m \angle1=(2x−5)^{\circ}\) and \(m \angle8=(x)^{\circ}\)
For 7-10, determine whether the statement is true or false.
- Alternate exterior angles are always congruent.
- If alternate exterior angles are congruent then lines are parallel.
- Alternate exterior angles are on the interior of two lines.
- Alternate exterior angles are on opposite sides of the transversal.
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.5.
Resources
Vocabulary
| Term | Definition |
|---|---|
| alternate exterior angles | Alternate exterior angles are two angles that are on the exterior of two different lines, but on the opposite sides of the transversal. |
Additional Resource
Interactive Element
Video: Alternate Exterior Angles Principles - Basic
Activities: Alternate Exterior Angles Discussion Questions
Study Aids: Angles and Transversals Study Guide
Practice: Alternate Exterior Angles
Real World: Alternate Exterior Angles

