Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Home
Bookshelves
Mathematics
Geometry
3: Lines
3.7: Same Side Interior Angles

3.7: Same Side Interior Angles

Last updated

Jun 15, 2022
Save as PDF
- 3.6: Alternate Exterior Angles
- 3.8: Angles and Perpendicular Lines

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Angles on the same side of a transversal and inside the lines it intersects.

Same side interior angles are two angles that are on the same side of the transversal and on the interior of (between) the two lines.

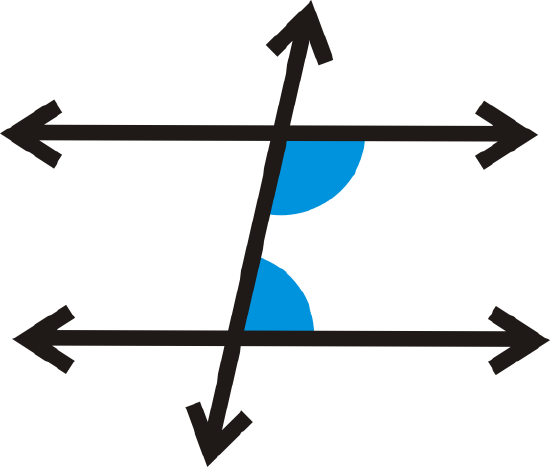
f-d_a8d9b91df19f74f34fa164377fd63a7dbc7c055fc5ff57ecbe9634bf+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{1}$

Same Side Interior Angles Theorem: If two parallel lines are cut by a transversal, then the same side interior angles are supplementary.

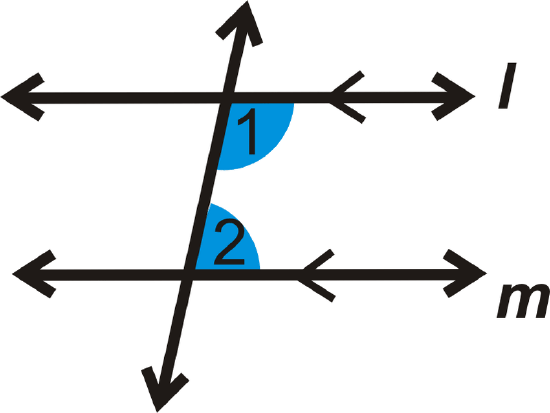
f-d_91ce9eaa5c4a427538d80d88915519d0a21cfbabb9534f1f08cb0850+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{2}$

If $l \parallel m$ , then $m\angle 1+m\angle 2=180^{\circ}$ .

Converse of the Same Side Interior Angles Theorem: If two lines are cut by a transversal and the same side interior angles are supplementary, then the lines are parallel.

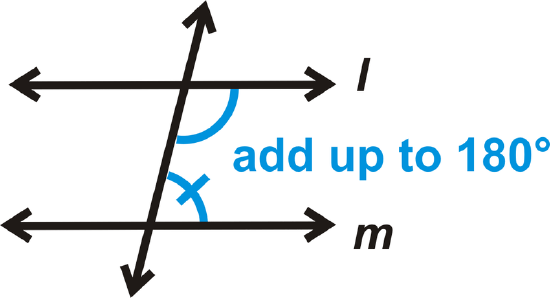
f-d_67d340685341a2f8c3028d57936483cd844c7c3451729fd0f1cfc6b0+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{3}$

then $l \parallel m$

Suppose you were presented with two angles that are on the same side of a transversal and between the two parallel lines crossed by the transversal. How would you describe these angles and what could you conclude about their measures?

Example $\PageIndex{1}$

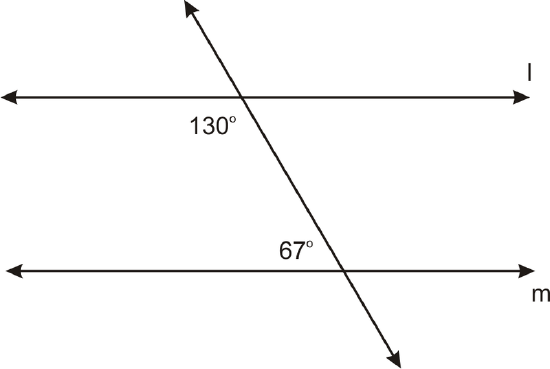
Is $l \parallel m$ ? How do you know?

Solution

These angles are Same Side Interior Angles. So, if they add up to $180^{\circ}$ , then $l\parallel m$ .

$130^{\circ}+67^{\circ}=197^{\circ}$ , therefore the lines are not parallel.

f-d_74e7e9a69fe84ce8ccc252f406f9133f3718d58847748e2a3b59e5a1+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{4}$

Example $\PageIndex{2}$

Give two examples of same side interior angles in the diagram:

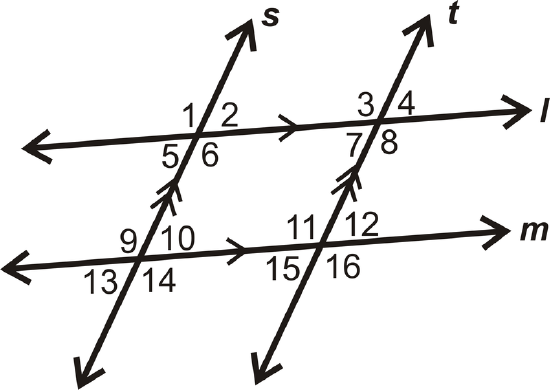
f-d_acf685f70adc87b4075812b7ecc116dbceabac3970f8ed695303c88b+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{5}$

Solution

There are MANY examples of same side interior angles in the diagram. Two are $\angle 6$ and $\angle 10$ , and $\angle 8$ and $\angle 12$ .

Example $\PageIndex{3}$

Find the value of $x$ .

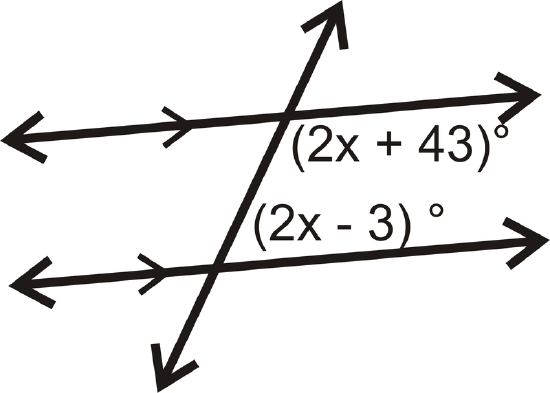
f-d_44014a86cf753c8bea839356ae4c8b578df175e0f1e2aab4cdf96ccc+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{6}$

Solution

The given angles are same side interior angles. Because the lines are parallel, the angles add up to $180^{\circ}$ .

$\begin{align*}(2x+43)^{\circ}+(2x−3)^{\circ} &=180^{\circ} \\ (4x+40)^{\circ} &=180^{\circ} \\ 4x &=140 \\ x &=35\end{align*}$

Example $\PageIndex{4}$

Find the value of $y$ .

f-d_ef9c9e5e1682147552c76009265b7367a902b7a14102006cb31b7352+IMAGE_TINY+IMAGE_TINY.png

Solution

$y$ is a same side interior angle with the marked right angle. This means that $90^{\circ}+y=180$ so $y=90$ .

Example $\PageIndex{5}$

Find the value of $x$ if $m\angle 3=(3x+12)^{\circ}$ and $m\angle 5=(5x+8)^{\circ}$ .

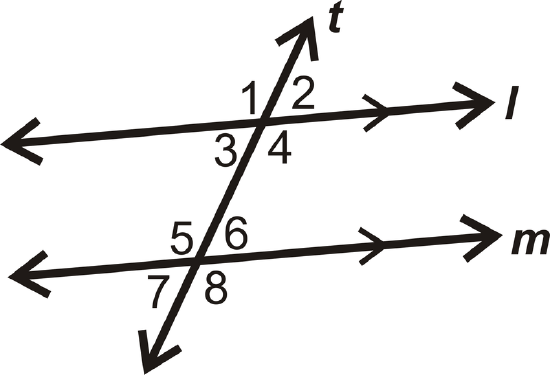
f-d_7d690a17ce6b2e3bc2ec2070038ceed705eb9a6272064c8c84195102+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{8}$

Solution

These are same side interior angles, so set up an equation and solve for $x$ . Remember that same side interior angles add up to $180^{\circ}$ .

$\begin{align*} (3x+12)^{\circ}+(5x+8)^{\circ} &=180^{\circ} \\(8x+20)^{\circ} &=180^{\circ} \\8x &=160 \\ x &=20 \end{align*}$

Review

For questions 1-2, use the diagram to determine if each angle pair is congruent, supplementary or neither.

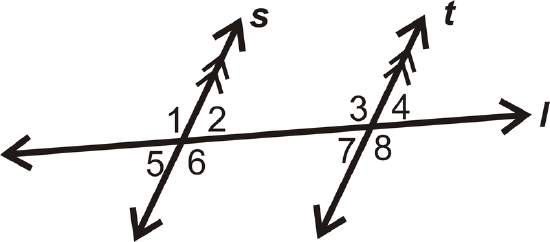
f-d_c433bbb430c5a21eef1034baabdc9ea175e53f1b202b64c654c172d5+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{9}$

$\angle 5$ and $\angle 8$
$\angle 2$ and $\angle 3$
Are the lines parallel? Justify your answer.

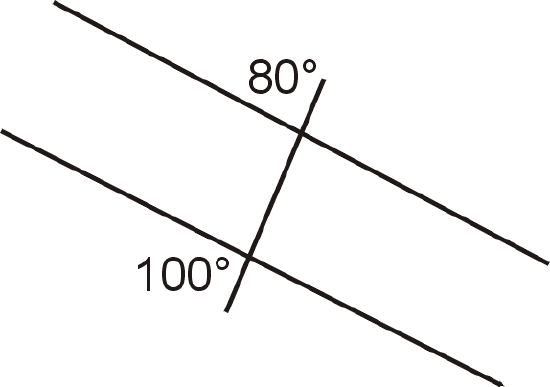
Figure $\PageIndex{10}$

In 4-5, use the given information to determine which lines are parallel. If there are none, write none. Consider each question individually.

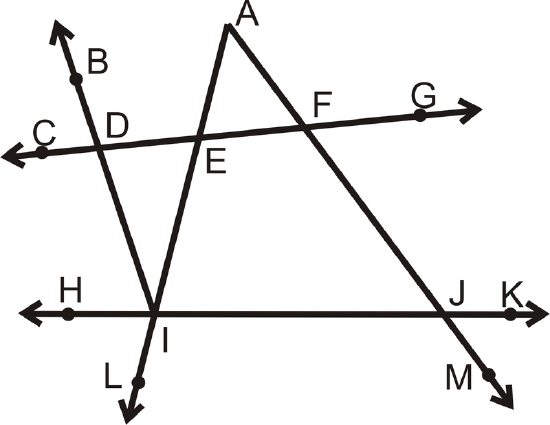
f-d_a9669d1041f370e9e54907e878108a83838d6cf9377d8d1f8aac5a10+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{11}$

$\angle AFD$ and $\angle BDF$ are supplementary
$\angle DIJ$ and $\angle FJI$ are supplementary

For 6-8, what does the value of $x$ have to be to make the lines parallel?

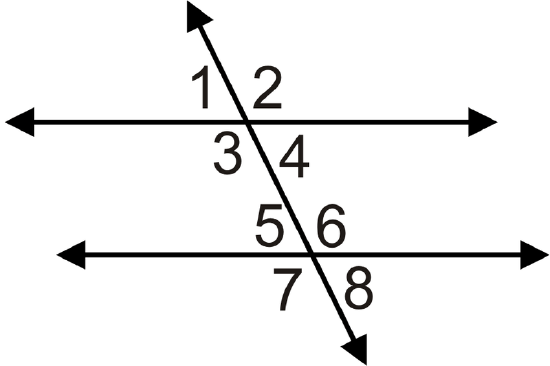
f-d_963dbdfc7b826d8117ff8f1171f6c6bf93e5c8d514fd8352bb797b67+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{12}$

$m\angle 3=(3x+25)^{\circ}$ and $m\angle 5=(4x−55)^{\circ}$
$m\angle 4=(2x+15)^{\circ}$ and $m\angle 6=(3x−5)^{\circ}$
$m\angle 3=(x+17)^{\circ}$ and $m\angle 5=(3x−5)^{\circ}$

For 9-10, determine whether the statement is true or false.

Same side interior angles are on the same side of the transversal.
Same side interior angles are congruent when lines are parallel.

Review (Answers)

To see the Review answers, open this PDF file and look for section 3.6.

Vocabulary

Term	Definition
same side interior angles	Same side interior angles are two angles that are on the same side of the transversal and on the interior of the two lines.
supplementary angles	Two angles that add up to $180^{\circ}$ .
transversal	A line that intersects two other lines.

Additional Resource

Interactive Element

Video: Same Side Interior Angles Principles - Basic

Activities: Same Side Interior Angles Discussion Questions

Study Aids: Angles and Transversals Study Guide

Practice: Same Side Interior Angles

Real World: Alternate Exterior Angles

Review

Review (Answers)

Vocabulary

Additional Resource

Support Center

How can we help?